The magnetic field existing in a region is gicen by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
2B0Il
zero
B0Il
4B0Il
The correct Answer is:C
To solve the problem, we need to find the net magnetic force experienced by a square loop carrying a current I in a magnetic field defined by →B=B0(1+xl)^k. The loop has an edge length l and is oriented with its edges parallel to the x-y axes.
1. Identify the Magnetic Field at Different Edges of the Loop:
- The magnetic field is given by →B=B0(1+xl)^k.
- For the edge AB (where x=0):
B1=B0(1+0l)=B0
- For the edge CD (where x=l):
B2=B0(1+ll)=B0(1+1)=2B0
2. Determine the Magnetic Force on Each Edge:
- The magnetic force on a straight current-carrying conductor in a magnetic field is given by →F=I→L×→B.
- For edge AB (current flows in the positive y-direction):
→FAB=Il^j×B1^k=IlB0^i
- For edge CD (current flows in the negative y-direction):
→FCD=−Il^j×B2^k=−Il(2B0)^i=−2IlB0^i
3. Calculate the Net Force on the Loop:
- The forces on edges AD and BC will cancel each other out because the magnetic field does not vary along these edges (the magnetic field is the same at both edges).
- Therefore, the net force on the loop is:
→Fnet=→FCD+→FAB=(−2IlB0+IlB0)^i=−IlB0^i
- The magnitude of the net magnetic force is:
Fnet=|−IlB0|=IlB0
4. Conclusion:
- The magnitude of the net magnetic force experienced by the loop is:
Fnet=IlB0
Answer:
The magnitude of the net magnetic force experienced by the loop is IlB0.
- The magnetic field is given by →B=B0(1+xl)^k.
- For the edge AB (where x=0):
B1=B0(1+0l)=B0
- For the edge CD (where x=l):
B2=B0(1+ll)=B0(1+1)=2B0
- The magnetic force on a straight current-carrying conductor in a magnetic field is given by →F=I→L×→B.
- For edge AB (current flows in the positive y-direction):
→FAB=Il^j×B1^k=IlB0^i
- For edge CD (current flows in the negative y-direction):
→FCD=−Il^j×B2^k=−Il(2B0)^i=−2IlB0^i
- The forces on edges AD and BC will cancel each other out because the magnetic field does not vary along these edges (the magnetic field is the same at both edges).
- Therefore, the net force on the loop is:
→Fnet=→FCD+→FAB=(−2IlB0+IlB0)^i=−IlB0^i
- The magnitude of the net magnetic force is:
Fnet=|−IlB0|=IlB0
- The magnitude of the net magnetic force experienced by the loop is:
Fnet=IlB0
The magnitude of the net magnetic force experienced by the loop is IlB0.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
The magnetic field existing in a region is given by ,B=B0(xL+x2L2)ˆk.A square loop edge L carrying a current I is placed with its parallel to the X and Y-axis Find the net magnetic force experienced by the loop
View SolutionThe magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
View SolutionA hypthetical magnetic field existing in a region is given by →B=B0→er, where →–––r denotes the uit vector along the redial direction. A circular loop of radus a, carrying a current I, is placed with its plane parallel to the x-y plane and the centre at (0,0, d) .Find the magnitude of the magnetic force acting on the loop.
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionThe magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is

View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
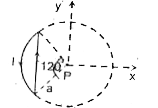
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution
