Assertion In a uniform magnetic field B=B0ˆk, if velocity of a charged particle is v0ˆi at t = 0, then it can have the velocity v0ˆj at some other instant.
Reason In uniform magnetic field, acceleration of a charged particle is always zero.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:c
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
Step 1: Understand the Assertion
The assertion states that in a uniform magnetic field B=B0^k, if the velocity of a charged particle is v=v0^i at t=0, then it can have the velocity v=v0^j at some other instant.
Analysis: In a uniform magnetic field, the magnetic force acts perpendicular to both the velocity of the charged particle and the magnetic field direction. This means that the magnetic force can change the direction of the velocity but not its magnitude. Therefore, if the particle starts with a velocity in the ^i direction, it cannot spontaneously change to a velocity in the ^j direction without an external force acting on it. Thus, the assertion is false.
Step 2: Understand the Reason
The reason states that in a uniform magnetic field, the acceleration of a charged particle is always zero.
Analysis: This statement is not entirely accurate. While it is true that in a uniform magnetic field, the magnetic force does not do work on the charged particle (since the force is always perpendicular to the displacement), the particle can still experience centripetal acceleration if it moves in a circular path due to the magnetic force. However, if we consider the net force acting on the particle, it can be zero if the particle moves with constant velocity. Therefore, the reason is true in the context that the net acceleration in the direction of motion is zero, but it can have centripetal acceleration if it is moving in a circular path.
Conclusion
- Assertion: False
- Reason: True
Final Answer
The assertion is false, but the reason is true.
---
The assertion states that in a uniform magnetic field B=B0^k, if the velocity of a charged particle is v=v0^i at t=0, then it can have the velocity v=v0^j at some other instant.
The reason states that in a uniform magnetic field, the acceleration of a charged particle is always zero.
- Assertion: False
- Reason: True
The assertion is false, but the reason is true.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A charged particle of specific charge (i.e.,Charge per unit mass 0 0.2 C/kg has velocity 2ˆi−3ˆjms−1 at some instant in a uniform magnetic field 5ˆi+2ˆj (tesla).Find the acceleration of the particle at this instant
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionAssertion In non-uniform magnetic field speed of a charged particle varies.
Reason Work done by magnetic force on a charged particle is always zero.
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionThere exists a uniform magnetic field →B=+B0ˆk for x>0and→B=0 for all x<0. A charged particle placed at (0,−a,0) is given an initial velocity →v=v0ˆi. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at (0,−a,0) must be towards y-axis
View SolutionAs a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
Motion of charged particle will be along a helical path with
View SolutionA charged particle of specific charge (i.e charge per unit mass) 0.2 C/kg has velocity 2ˆi−3ˆj (m/s) at some instant in a uniform magnetic field 5ˆi+2ˆj (tesla). Find the acceleration of the particle at this instant
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
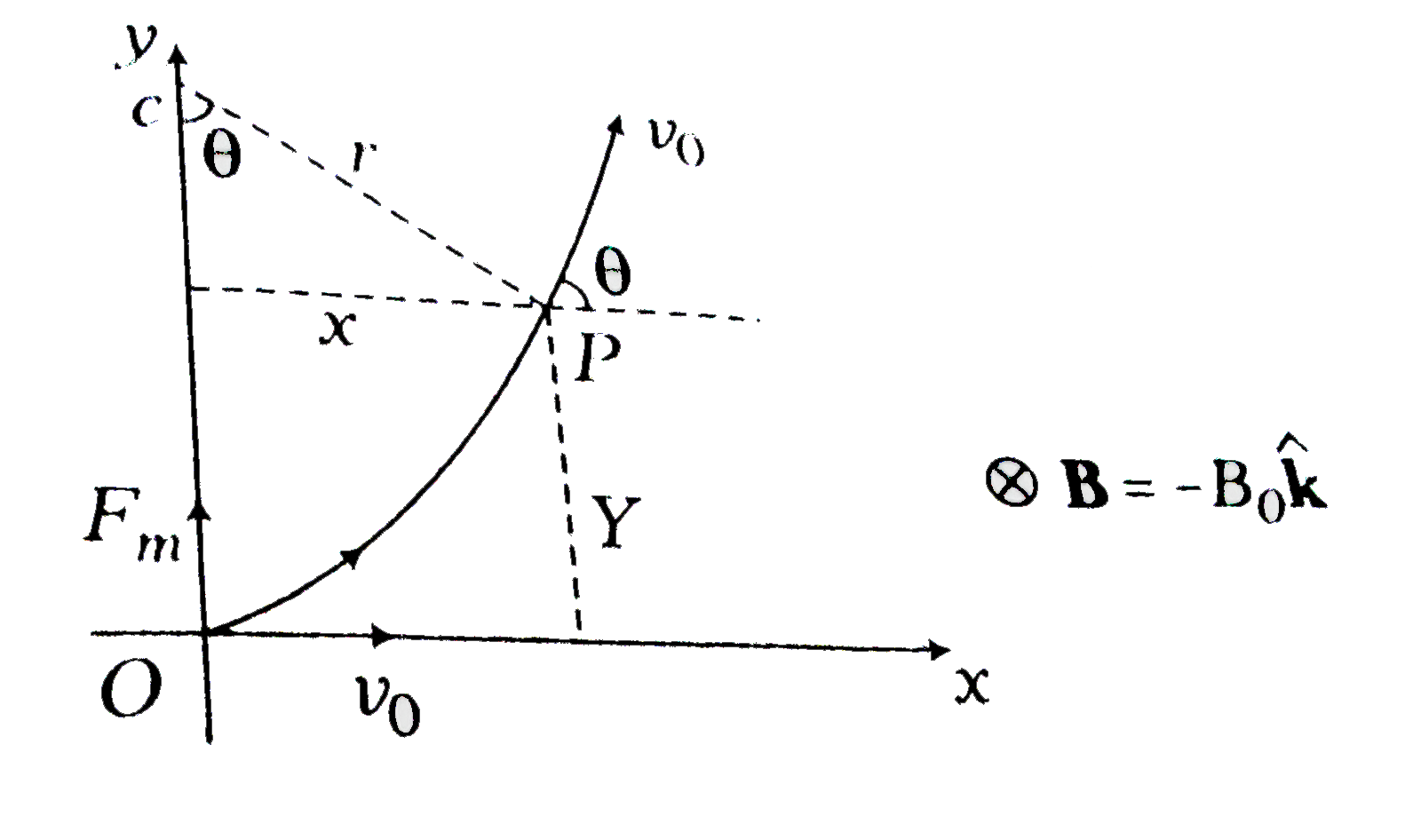
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionAs a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
If the coordinates of the particle at t = 0 are (2 m, 1 m, 0), coordinates at a time t = 3 T, where T is the time period of circular component of motion. will be (take π=3.14)
View Solution
