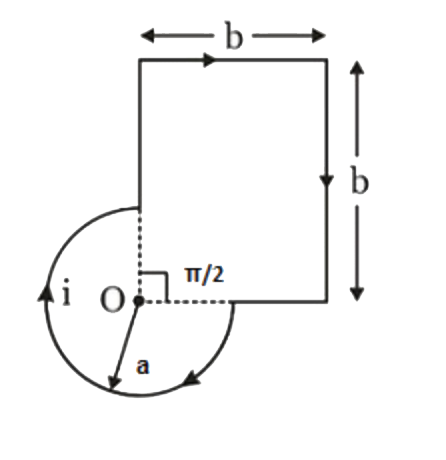
Assertion At the centre of a circular current carrying loop (I1), there is an infinitely long straight of the circle. Then magnetic force of attraction between two is zero.
Reason Magnetic field of I1 at centre is inwards, parallel to I2.
The correct Answer is:a
To solve the problem, we need to analyze the assertion and reason provided in the question regarding the magnetic field and forces between a circular current-carrying loop and an infinitely long straight wire.
1. Understanding the Setup:
- We have a circular loop carrying a current I1 and an infinitely long straight wire carrying a current I2 placed at the center of the loop.
2. Magnetic Field at the Center of the Loop:
- The magnetic field B at the center of a circular loop carrying current I1 can be determined using the right-hand rule. If the current flows in a clockwise direction, the magnetic field at the center will point downwards (into the plane). If it flows counterclockwise, the magnetic field will point upwards (out of the plane).
3. Direction of the Magnetic Field:
- According to the assertion, the magnetic field at the center of the loop is directed inward (which corresponds to a clockwise current). This is consistent with the right-hand rule, where curling the fingers in the direction of the current gives the direction of the magnetic field.
4. Force on the Straight Wire:
- The magnetic force F on a current-carrying conductor in a magnetic field is given by the formula:
F=IL×B
- Here, I is the current in the wire, L is the length of the wire segment in the magnetic field, and B is the magnetic field strength. The direction of the force is determined by the angle θ between the current direction in the wire and the magnetic field direction.
5. Angle Between Current and Magnetic Field:
- If the current I2 in the straight wire is parallel to the magnetic field B (both pointing in the same direction) or anti-parallel (pointing in opposite directions), the angle θ is either 0∘ or 180∘.
- In both cases, sinθ=0, leading to:
F=I2LBsinθ=0
- Therefore, the magnetic force of attraction between the loop and the straight wire is zero.
6. Conclusion:
- The assertion is true: the magnetic force of attraction between the circular loop and the straight wire is zero.
- The reason is also true: the magnetic field at the center of the loop is inward and parallel to the current in the wire.
Final Answer:
Both the assertion and the reason are true, and the reason correctly explains the assertion.
---
- We have a circular loop carrying a current I1 and an infinitely long straight wire carrying a current I2 placed at the center of the loop.
- The magnetic field B at the center of a circular loop carrying current I1 can be determined using the right-hand rule. If the current flows in a clockwise direction, the magnetic field at the center will point downwards (into the plane). If it flows counterclockwise, the magnetic field will point upwards (out of the plane).
- According to the assertion, the magnetic field at the center of the loop is directed inward (which corresponds to a clockwise current). This is consistent with the right-hand rule, where curling the fingers in the direction of the current gives the direction of the magnetic field.
- The magnetic force F on a current-carrying conductor in a magnetic field is given by the formula:
F=IL×B
- Here, I is the current in the wire, L is the length of the wire segment in the magnetic field, and B is the magnetic field strength. The direction of the force is determined by the angle θ between the current direction in the wire and the magnetic field direction.
- If the current I2 in the straight wire is parallel to the magnetic field B (both pointing in the same direction) or anti-parallel (pointing in opposite directions), the angle θ is either 0∘ or 180∘.
- In both cases, sinθ=0, leading to:
F=I2LBsinθ=0
- Therefore, the magnetic force of attraction between the loop and the straight wire is zero.
- The assertion is true: the magnetic force of attraction between the circular loop and the straight wire is zero.
- The reason is also true: the magnetic field at the center of the loop is inward and parallel to the current in the wire.
Both the assertion and the reason are true, and the reason correctly explains the assertion.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
Knowledge Check
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
A(BA)2μ0πBBA√Aμ0CBA√Aμ0πD2BA√Aμ0√π
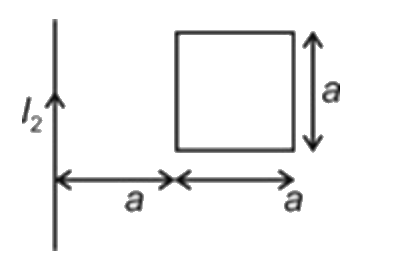
In the diagram shown, I1,I2 are the magnitudes of current in the squre loop and infinite long straight conductor respectively. If the net magnetic field at the centre of the loop is zero, then the relation between I1andI2 is
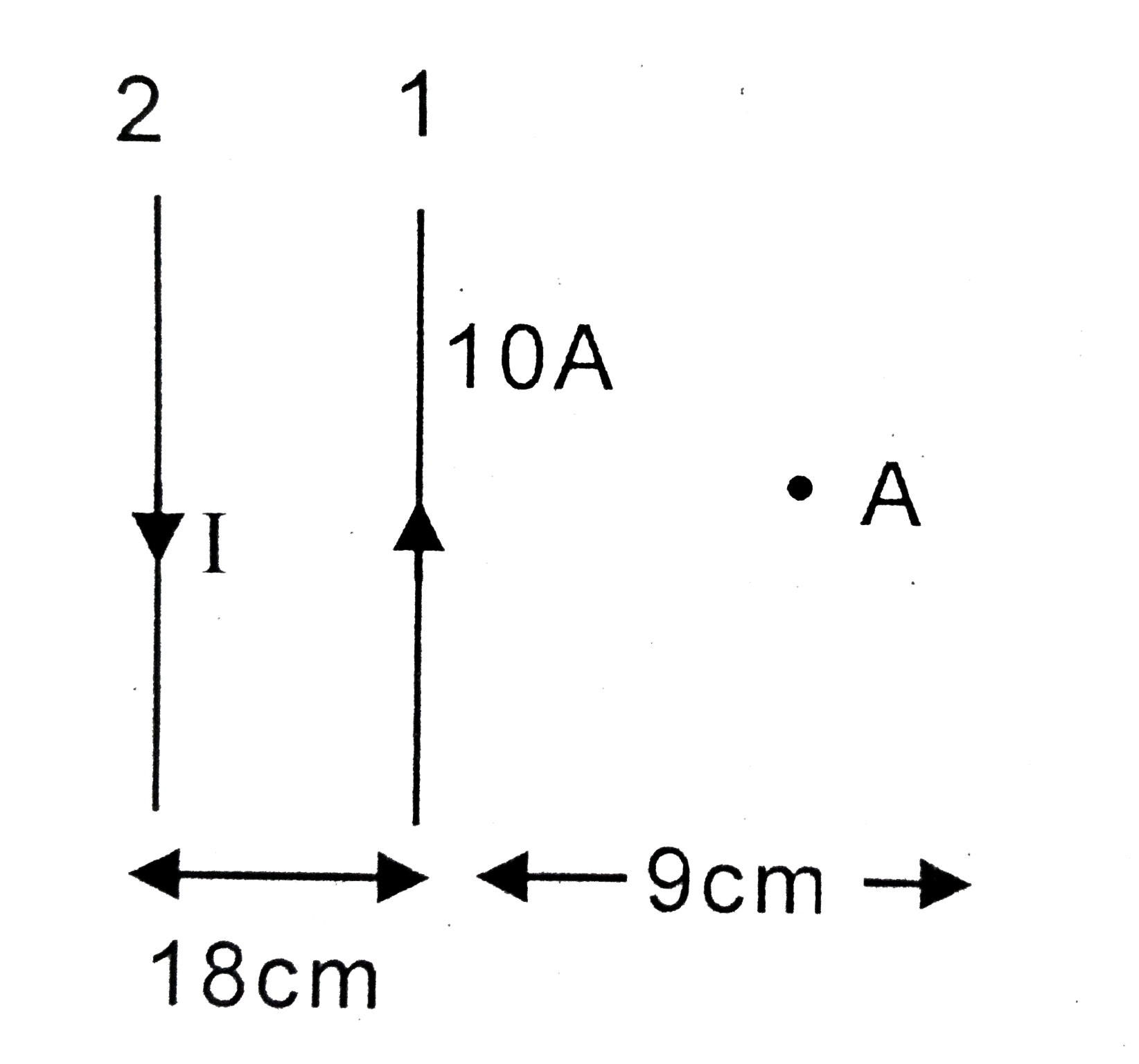
View SolutionIn figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
View SolutionMagnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
View SolutionAssertion Net torque in the current carrying loop placed in a uniform magnetic field (pointing inwards) is zero.

Reasonl Magnetic moment (M) is inwards.
View SolutionA triangular loop (ABC) having current i2 and an infinite wire having current i1 are placed in the same plane.Find the magnetic force of interaction between the infinite wire and the loop ABC.

View SolutionThe magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View Solution