A metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
B2l2vr
Blvr
B2lvr
Blv2r
The correct Answer is:a
To find the force required to move a metal rod of length l across a uniform magnetic field B with a velocity v, we can follow these steps:
1. Identify the Induced EMF:
The induced electromotive force (EMF) E in the rod moving through the magnetic field can be calculated using the formula:
E=B⋅l⋅v
where B is the magnetic field strength, l is the length of the rod, and v is the velocity of the rod.
Hint: Remember that the induced EMF is generated due to the motion of the conductor in the magnetic field.
2. Calculate the Current:
The current I flowing through the circuit can be calculated using Ohm's law:
I=Er=B⋅l⋅vr
where r is the resistance of the circuit.
Hint: Use Ohm's law to relate EMF, current, and resistance.
3. Determine the Magnetic Force:
The magnetic force FB acting on the rod due to the current in the magnetic field can be calculated using the formula:
FB=B⋅I⋅l
Substituting the expression for current I:
FB=B⋅(B⋅l⋅vr)⋅l=B2⋅l2⋅vr
Hint: The magnetic force on a current-carrying conductor in a magnetic field is given by the product of the magnetic field, the current, and the length of the conductor.
4. Force Required to Move the Rod:
To keep the rod moving with a constant velocity v, we need to apply an external force F that is equal in magnitude but opposite in direction to the magnetic force FB:
F=FB=B2⋅l2⋅vr
Hint: The applied force must counteract the magnetic force to maintain constant velocity.
Final Answer:
The force required to move the rod is:
F=B2⋅l2⋅vr
The induced electromotive force (EMF) E in the rod moving through the magnetic field can be calculated using the formula:
E=B⋅l⋅v
where B is the magnetic field strength, l is the length of the rod, and v is the velocity of the rod.
The current I flowing through the circuit can be calculated using Ohm's law:
I=Er=B⋅l⋅vr
where r is the resistance of the circuit.
The magnetic force FB acting on the rod due to the current in the magnetic field can be calculated using the formula:
FB=B⋅I⋅l
Substituting the expression for current I:
FB=B⋅(B⋅l⋅vr)⋅l=B2⋅l2⋅vr
To keep the rod moving with a constant velocity v, we need to apply an external force F that is equal in magnitude but opposite in direction to the magnetic force FB:
F=FB=B2⋅l2⋅vr
The force required to move the rod is:
F=B2⋅l2⋅vr
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
Similar Questions
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionA metallic rod completes its circuit as shown in the figure. The circuit is normal to a magnetic field of B=0.15 tesla. If the resistances of the rod is 3Ω the force required to move the rod with a constant velocity of 2m/sec is-

A. 3.75×10−3N
B. 3.75×10−2N
C. 3.75×102N
D. 3.75×10−4N
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View SolutionAs shown in figure, a metal rod completes the circuit. The circuit area is perpendicular to a magnetic field with B=0.15T. If the resistance of the total circuit is 3Ω, how large a force is needed to move the rod as indicated with a constant speed of 2 m/s?
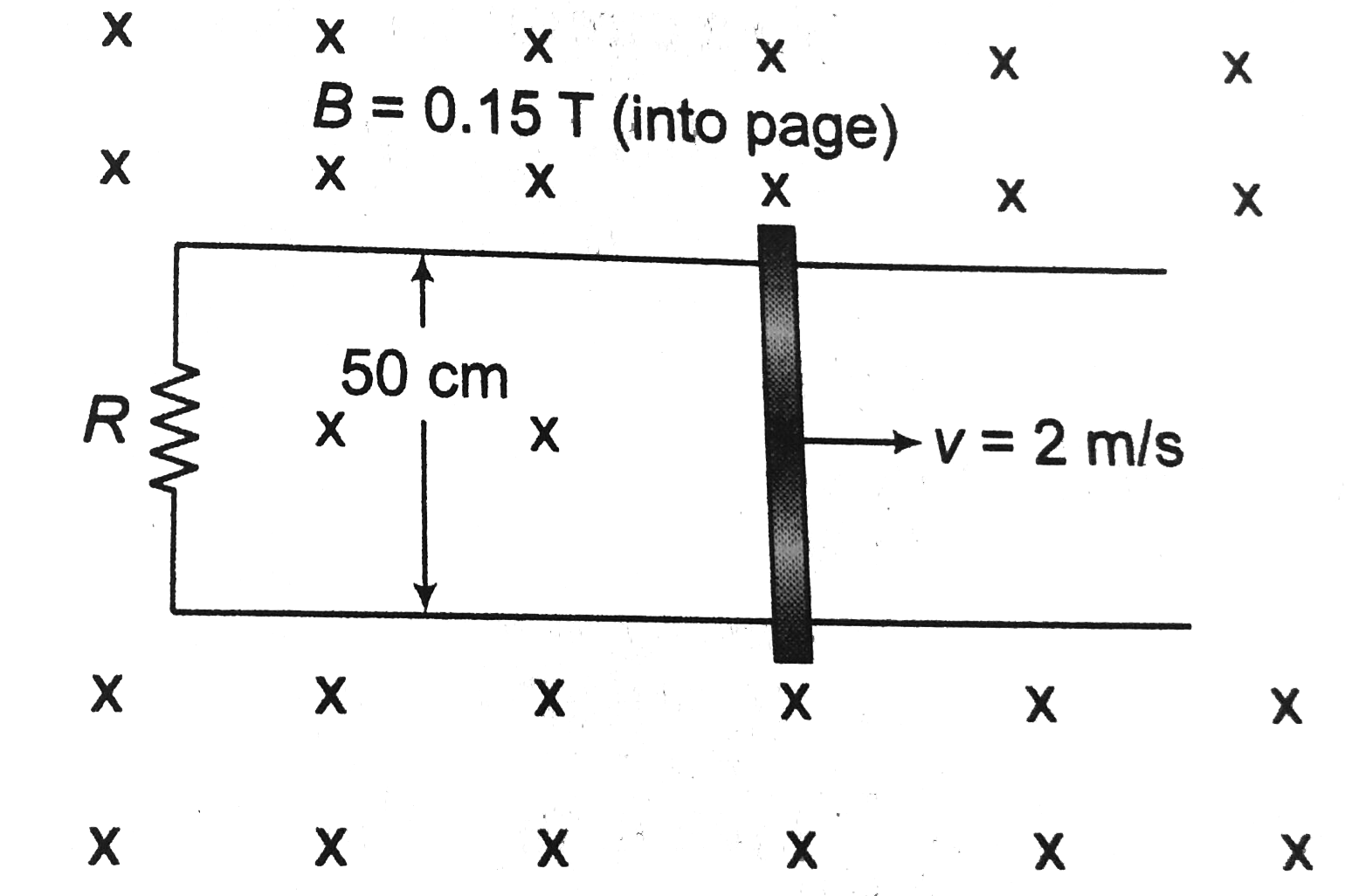
View SolutionA 0.5m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15T. If the resistance of the total circuit is 3Ω calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1
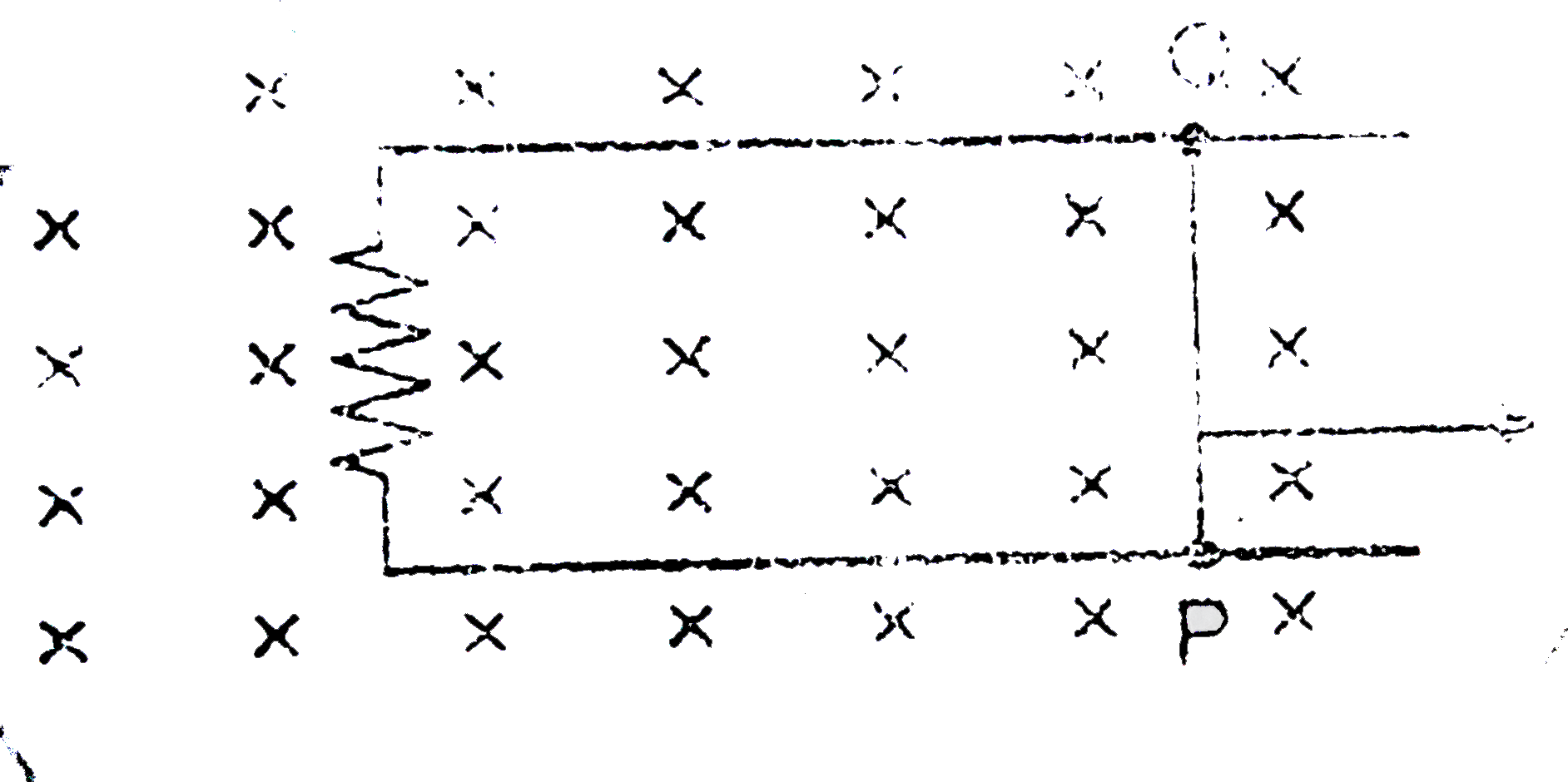
View SolutionThe figure shows a metal rod (PQ), which makes contact and complete the circuit. The circuit is perpendicular to the magnetic field withB=1T. If the resistance is 2Ω , then force required to move the rod and indicated with a constant speed of 2msis

View SolutionA conducting wire of length l is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current I is established in the rod are observed to be F1 and F2(<F1) for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)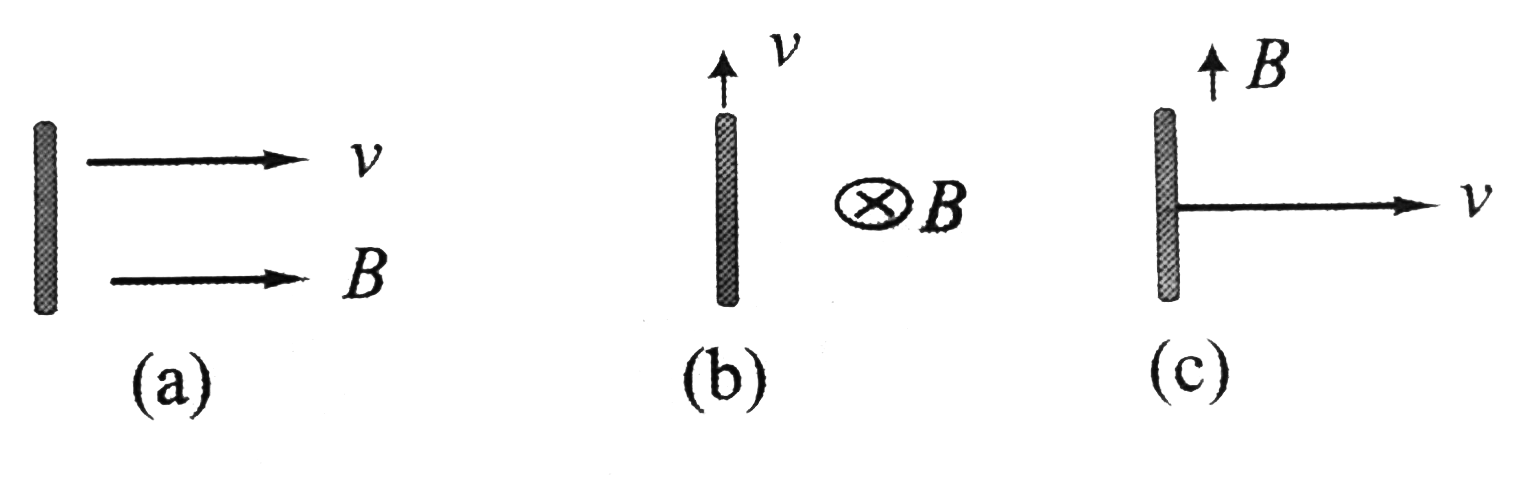
View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View Solution