A conducting wire of length l is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current I is established in the rod are observed to be F1 and F2(<F1) for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
To solve the problem, we need to analyze the forces acting on the conducting wire placed on a rough horizontal surface in a magnetic field. We will derive the expressions for the weight of the rod and the coefficient of friction step by step.
1. Identify the Forces Acting on the Rod:
- The weight of the rod W=mg acts downward.
- The normal force N acts upward.
- The magnetic force Fm acts on the rod due to the current in the presence of the magnetic field.
2. Magnetic Force Calculation:
- The magnetic force Fm acting on the rod can be calculated using the formula:
Fm=I⋅L⋅B⋅sin(θ)
- Since the magnetic field B is perpendicular to the length of the wire, θ=90∘ and sin(90∘)=1:
Fm=I⋅L⋅B
3. Force Required to Move the Rod:
- When the current I flows in one direction (let's say inward), the magnetic force acts downward. The minimum force F1 required to move the rod is equal to the frictional force:
F1=μN
- The normal force in this case is:
N=mg+Fm=mg+I⋅L⋅B
- Therefore, substituting N into the equation for F1:
F1=μ(mg+I⋅L⋅B)
4. Considering the Opposite Direction of Current:
- When the current flows in the opposite direction (outward), the magnetic force acts upward. The minimum force F2 required to move the rod is:
F2=μN′
- The normal force in this case is:
N′=mg−Fm=mg−I⋅L⋅B
- Therefore, substituting N′ into the equation for F2:
F2=μ(mg−I⋅L⋅B)
5. Setting Up the Equations:
- We have two equations:
F1=μ(mg+I⋅L⋅B)(1)
F2=μ(mg−I⋅L⋅B)(2)
6. Dividing the Two Equations:
- Divide equation (1) by equation (2):
F1F2=μ(mg+I⋅L⋅B)μ(mg−I⋅L⋅B)
- Simplifying gives:
F1F2=mg+I⋅L⋅Bmg−I⋅L⋅B
7. Cross-Multiplying:
- Cross-multiplying gives:
F1(mg−I⋅L⋅B)=F2(mg+I⋅L⋅B)
8. Rearranging the Equation:
- Rearranging leads to:
F1mg−F1I⋅L⋅B=F2mg+F2I⋅L⋅B
- Collecting terms gives:
(F1−F2)mg=(F1+F2)I⋅L⋅B
9. Solving for Weight mg:
- Therefore, we can express the weight of the rod as:
mg=(F1−F2)(F1+F2)I⋅L⋅B
10. Finding the Coefficient of Friction μ:
- Substitute mg back into either equation (1) or (2) to find μ. Using equation (1):
F1=μ((F1−F2)(F1+F2)I⋅L⋅B+I⋅L⋅B)
- Rearranging gives:
μ=F1−F22I⋅L⋅B
Final Results:
- The weight of the rod is:
mg=(F1−F2)(F1+F2)I⋅L⋅B
- The coefficient of friction is:
μ=F1−F22I⋅L⋅B
- The weight of the rod W=mg acts downward.
- The normal force N acts upward.
- The magnetic force Fm acts on the rod due to the current in the presence of the magnetic field.
- The magnetic force Fm acting on the rod can be calculated using the formula:
Fm=I⋅L⋅B⋅sin(θ)
- Since the magnetic field B is perpendicular to the length of the wire, θ=90∘ and sin(90∘)=1:
Fm=I⋅L⋅B
- When the current I flows in one direction (let's say inward), the magnetic force acts downward. The minimum force F1 required to move the rod is equal to the frictional force:
F1=μN
- The normal force in this case is:
N=mg+Fm=mg+I⋅L⋅B
- Therefore, substituting N into the equation for F1:
F1=μ(mg+I⋅L⋅B)
- When the current flows in the opposite direction (outward), the magnetic force acts upward. The minimum force F2 required to move the rod is:
F2=μN′
- The normal force in this case is:
N′=mg−Fm=mg−I⋅L⋅B
- Therefore, substituting N′ into the equation for F2:
F2=μ(mg−I⋅L⋅B)
- We have two equations:
F1=μ(mg+I⋅L⋅B)(1)
F2=μ(mg−I⋅L⋅B)(2)
- Divide equation (1) by equation (2):
F1F2=μ(mg+I⋅L⋅B)μ(mg−I⋅L⋅B)
- Simplifying gives:
F1F2=mg+I⋅L⋅Bmg−I⋅L⋅B
- Cross-multiplying gives:
F1(mg−I⋅L⋅B)=F2(mg+I⋅L⋅B)
- Rearranging leads to:
F1mg−F1I⋅L⋅B=F2mg+F2I⋅L⋅B
- Collecting terms gives:
(F1−F2)mg=(F1+F2)I⋅L⋅B
- Therefore, we can express the weight of the rod as:
mg=(F1−F2)(F1+F2)I⋅L⋅B
- Substitute mg back into either equation (1) or (2) to find μ. Using equation (1):
F1=μ((F1−F2)(F1+F2)I⋅L⋅B+I⋅L⋅B)
- Rearranging gives:
μ=F1−F22I⋅L⋅B
- The weight of the rod is:
mg=(F1−F2)(F1+F2)I⋅L⋅B
- The coefficient of friction is:
μ=F1−F22I⋅L⋅B
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

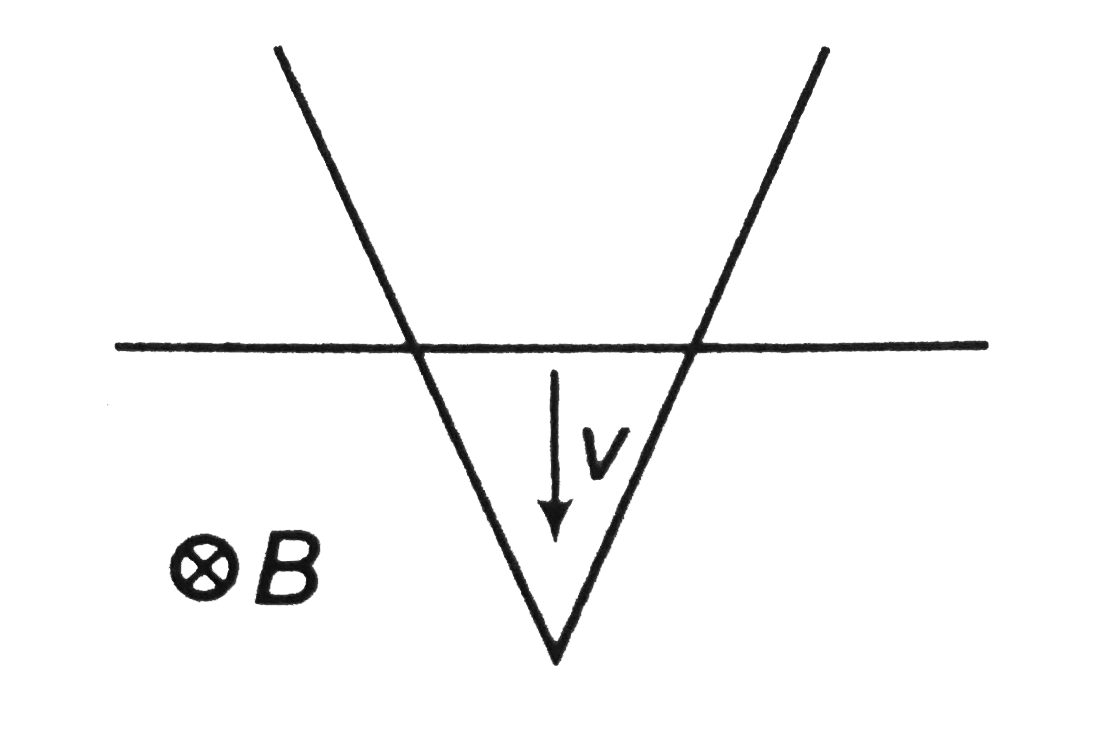
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View Solution
