The mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
To find the moment of inertia of a solid cylinder about a tangent to the cylinder, we can follow these steps:
1. Identify the Given Values:
- Mass of the cylinder, M=25kg
- Radius of the cylinder, R=5m
2. Moment of Inertia about the Center of Mass:
- The moment of inertia Icm of a solid cylinder about an axis through its center and perpendicular to its height is given by the formula:
Icm=12MR2
- Substituting the values:
Icm=12×25kg×(5m)2
Icm=12×25×25=6252=312.5kg m2
3. Apply the Parallel Axis Theorem:
- The parallel axis theorem states that:
IAB=Icm+Md2
- Here, d is the distance from the center of mass axis (CD) to the tangent axis (AB). Since the tangent touches the cylinder at its edge, d=R=5m.
4. Calculate the Moment of Inertia about the Tangent Axis:
- Substitute Icm and d into the parallel axis theorem:
IAB=Icm+MR2
IAB=312.5kg m2+25kg×(5m)2
IAB=312.5+25×25
IAB=312.5+625=937.5kg m2
5. Final Result:
- The moment of inertia of the solid cylinder about a tangent to the cylinder is:
IAB=937.5kg m2
- Mass of the cylinder, M=25kg
- Radius of the cylinder, R=5m
- The moment of inertia Icm of a solid cylinder about an axis through its center and perpendicular to its height is given by the formula:
Icm=12MR2
- Substituting the values:
Icm=12×25kg×(5m)2
Icm=12×25×25=6252=312.5kg m2
- The parallel axis theorem states that:
IAB=Icm+Md2
- Here, d is the distance from the center of mass axis (CD) to the tangent axis (AB). Since the tangent touches the cylinder at its edge, d=R=5m.
- Substitute Icm and d into the parallel axis theorem:
IAB=Icm+MR2
IAB=312.5kg m2+25kg×(5m)2
IAB=312.5+25×25
IAB=312.5+625=937.5kg m2
- The moment of inertia of the solid cylinder about a tangent to the cylinder is:
IAB=937.5kg m2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.120videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.220videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
What is moment of inertia of a cylinder of radius r, along its height?
View SolutionThe circumference of the base of a cylinder is 132 cm and its height 25 cm. Find the volume of the cylinder.
View SolutionThe sum of the radius of the base and height of a solid cylinder is 37m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
View SolutionThe sum of the radius of the base and height of a solid cylinder is 37m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
View SolutionThe sum of the height and the radius of a solid cylinder is 35 cm and its total surface area is 3080cm2, find the volume of the cylinder.
View SolutionThe circumference of the base of a cylinder is 132 cm and its height 25cm. Find the volume of the cylinder.
View SolutionThe circumference of the base of a cylinder is 132 cm and its height 25cm. Find the volume of the cylinder.
View SolutionA solid cylinder of radius R & length 3R is made of a metarial having density ρ . Now two hemispheres each of radius R is removed from two ends of cylinder as shown in figure. Determine the moment of inertia of this object about axis of cylinder?
 View Solution
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
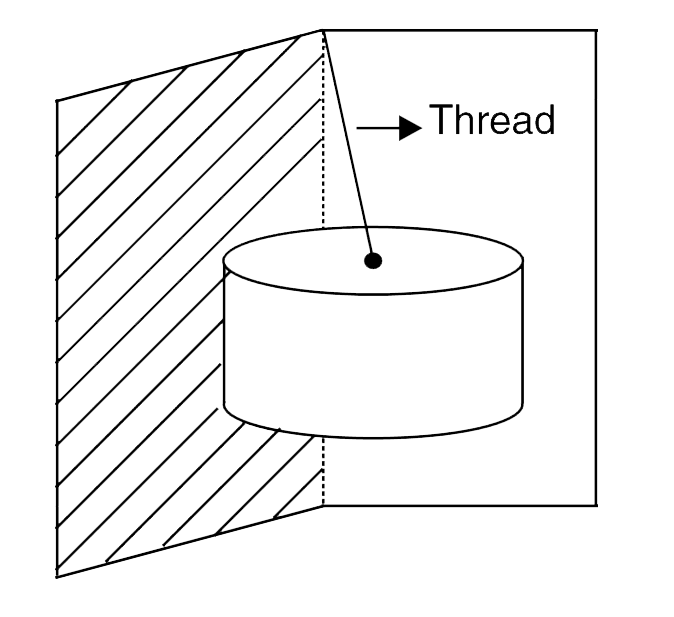 View Solution
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
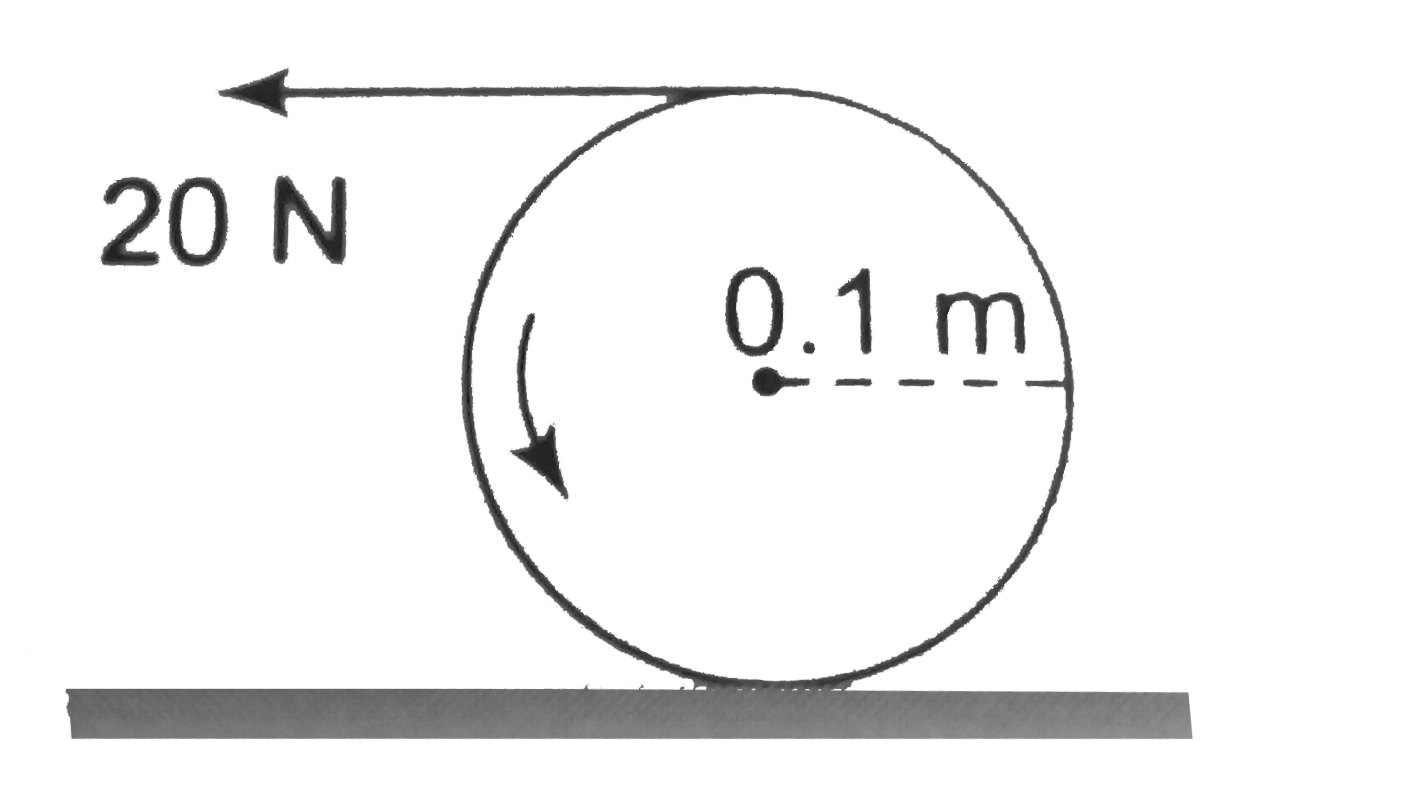 .View Solution
.View Solution

