What is moment of inertia of a cylinder of radius r, along its height?
a.
b.
c.
d.
The correct Answer is:B
To find the moment of inertia of a solid cylinder of radius r along its height (which is the axis passing through the center and perpendicular to the height), we can follow these steps:
Step 1: Understand the Moment of Inertia
The moment of inertia I of an object is a measure of its resistance to rotational motion about an axis. For a solid cylinder, the moment of inertia can be calculated using the formula for different axes.
Step 2: Identify the Axis of Rotation
In this case, we need to find the moment of inertia of the cylinder along its height. This means we are considering the axis that runs along the height of the cylinder, which is perpendicular to the circular base.
Step 3: Use the Formula for Moment of Inertia of a Cylinder
The moment of inertia I of a solid cylinder about its central axis (which is along its height) is given by the formula:
I=12mr2
where:
- m is the mass of the cylinder,
- r is the radius of the cylinder.
Step 4: Substitute the Values
Since we are looking for the moment of inertia along the height of the cylinder, we can directly substitute the values into the formula:
I=12mr2
Step 5: Conclusion
Thus, the moment of inertia of the cylinder along its height is:
I=mr22
Final Answer
The correct answer is mr22.
---
The moment of inertia I of an object is a measure of its resistance to rotational motion about an axis. For a solid cylinder, the moment of inertia can be calculated using the formula for different axes.
In this case, we need to find the moment of inertia of the cylinder along its height. This means we are considering the axis that runs along the height of the cylinder, which is perpendicular to the circular base.
The moment of inertia I of a solid cylinder about its central axis (which is along its height) is given by the formula:
I=12mr2
where:
- m is the mass of the cylinder,
- r is the radius of the cylinder.
Since we are looking for the moment of inertia along the height of the cylinder, we can directly substitute the values into the formula:
I=12mr2
Thus, the moment of inertia of the cylinder along its height is:
I=mr22
The correct answer is mr22.
Similar Questions
The moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionFind the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View SolutionThe moment of inertia of a solid sphere of radius R about its diameter is same as that of a disc of radius 2R about its diameter. The ratio of their masses is
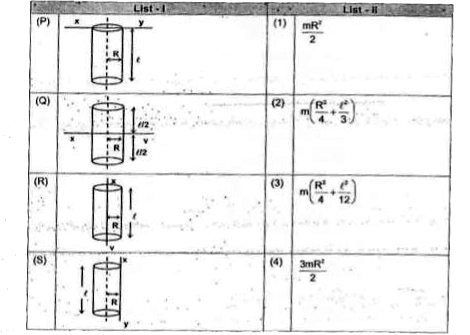
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is /. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionDefine moment of inertia and radius of gyration
View Solution
