A small ball of mass 1.0 kg is attached to one end of a 1.0 m long massless string and the other end of the string is hung from a point O. When the resulting pendulum is making 30∘ from the vertical, what is the magnitude of net torque about the point of suspension? [Take g=10m/s2]
To find the magnitude of the net torque about the point of suspension when the pendulum is at an angle of 30 degrees from the vertical, we can follow these steps:
1. Identify the Forces Acting on the Ball:
- The forces acting on the ball are:
- The gravitational force (weight) Fg=mg acting downward.
- The tension T in the string acting upward along the string.
2. Calculate the Weight of the Ball:
- Given:
- Mass m=1.0kg
- Acceleration due to gravity g=10m/s2
- The weight Fg is calculated as:
Fg=mg=1.0kg×10m/s2=10N
3. Determine the Length of the String:
- The length of the string L=1.0m.
4. Calculate the Perpendicular Distance from the Point of Suspension to the Line of Action of the Weight:
- When the pendulum is at an angle of 30∘ from the vertical, the perpendicular distance R from the point of suspension to the line of action of the weight can be calculated using the sine function:
R=Lsin(30∘)
- Since sin(30∘)=12:
R=1.0m×12=0.5m
5. Calculate the Torque due to the Weight:
- The torque τ about point O due to the weight is given by:
τ=Fg⋅R
- Substituting the values:
τ=10N×0.5m=5N m
6. Conclusion:
- The magnitude of the net torque about the point of suspension O is:
τ=5N m
- The forces acting on the ball are:
- The gravitational force (weight) Fg=mg acting downward.
- The tension T in the string acting upward along the string.
- Given:
- Mass m=1.0kg
- Acceleration due to gravity g=10m/s2
- The weight Fg is calculated as:
Fg=mg=1.0kg×10m/s2=10N
- The length of the string L=1.0m.
- When the pendulum is at an angle of 30∘ from the vertical, the perpendicular distance R from the point of suspension to the line of action of the weight can be calculated using the sine function:
R=Lsin(30∘)
- Since sin(30∘)=12:
R=1.0m×12=0.5m
- The torque τ about point O due to the weight is given by:
τ=Fg⋅R
- Substituting the values:
τ=10N×0.5m=5N m
- The magnitude of the net torque about the point of suspension O is:
τ=5N m
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A small ball of mass 1.0 kg is attached to one end of a 1.0 m long massless string and te other end of the string is hung from a point O. When the resulting pendulum is making 30∘C from the vertical, what is the magnitude of net torque about the point of suspension? [Take g=10m/s2]
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
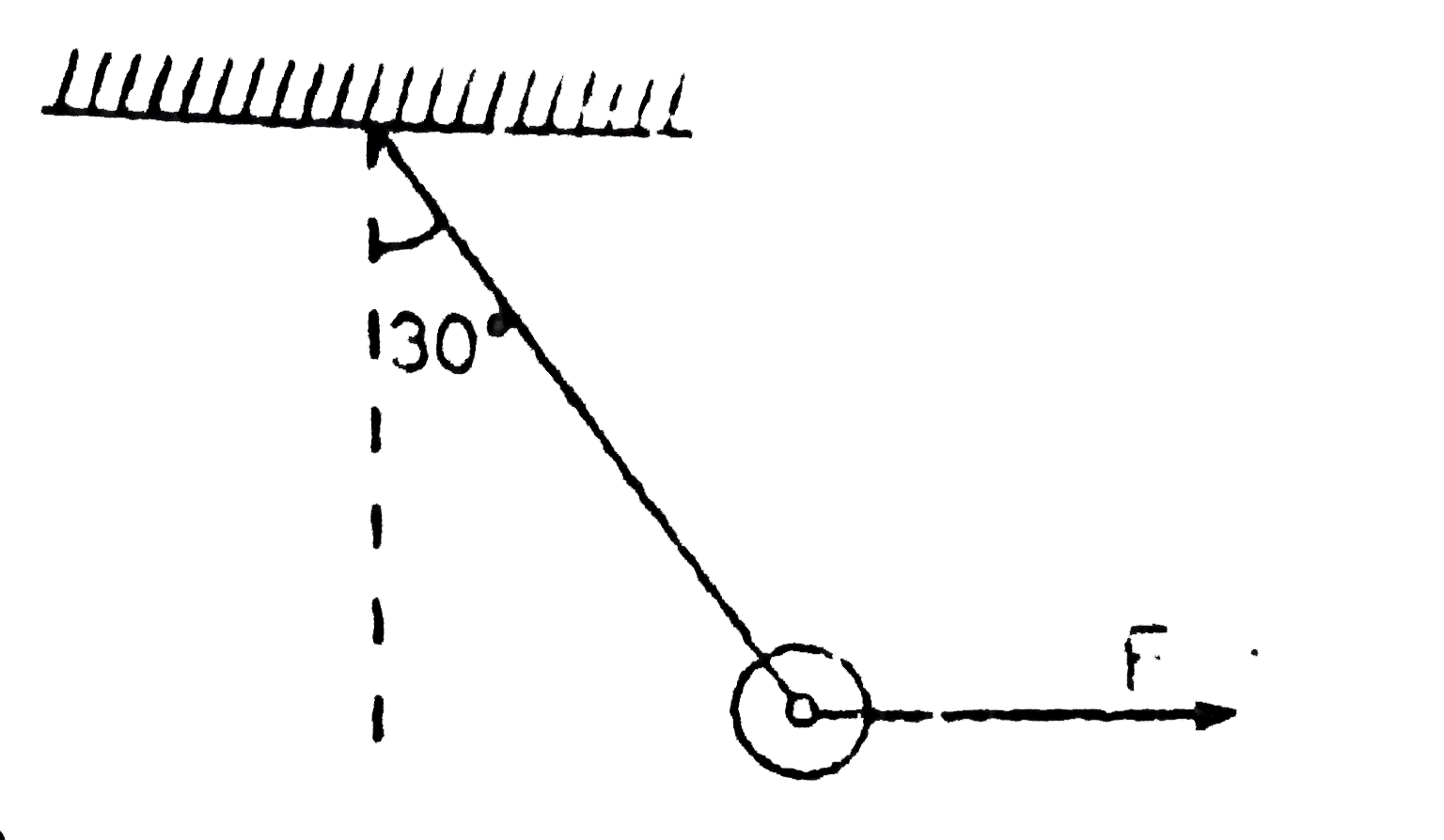 .
.
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionAn object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
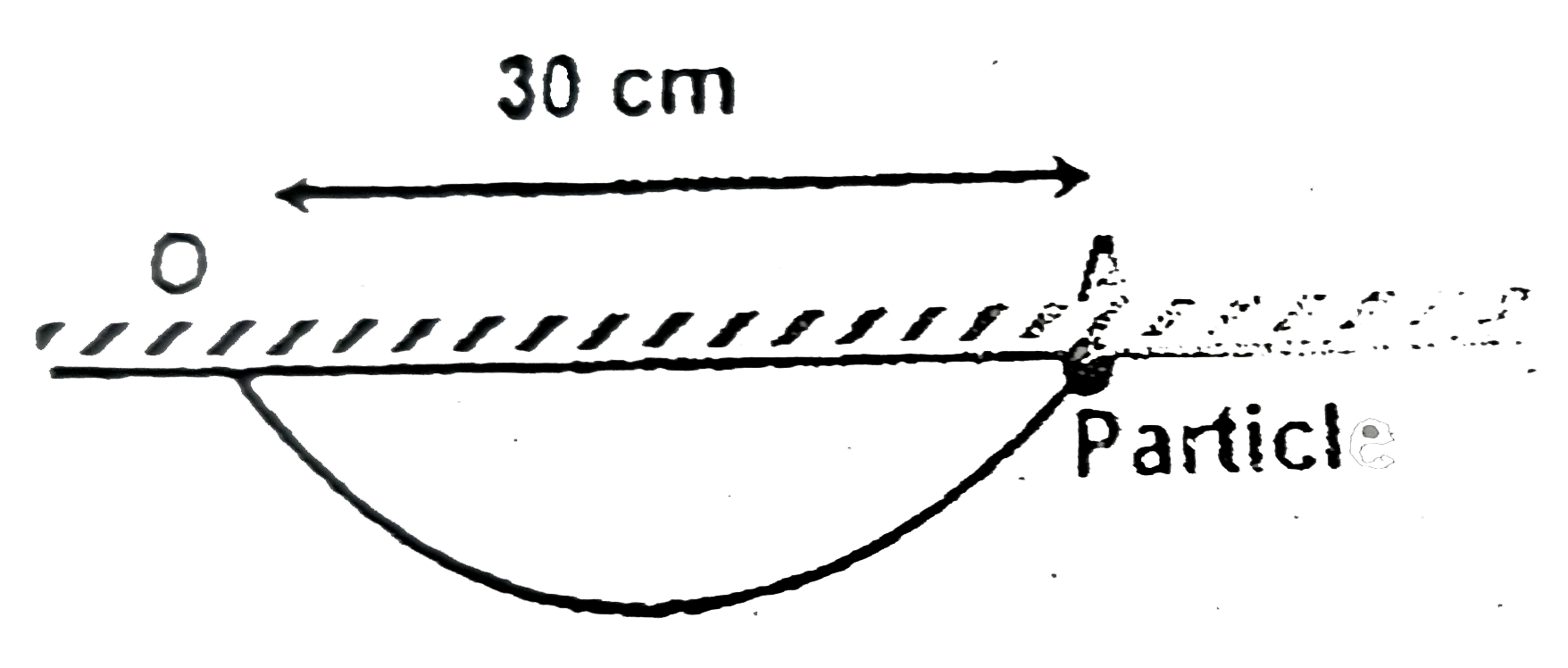
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
View SolutionA rod of mass 5 kg is connected to the string at point B. The span of rod is along horizontal. The other end of the rod is hinged at point A. If the string is massless, then the reaction of hinge at the instant when string is cut, is (Take, g=10ms−2)
View SolutionA ball of mass m is attached to a string whose other end is fixed. The system is free to rotate in vertical plane. When the ball swings, no work is done on the ball by the tension in the string. Which of the following statement is the correct explanation?
View SolutionA ball of mass 'm' is suspended from a point with a massless string of length l in form of a pendulum. This ball is given a horizontal velocity √4gl at bottom most point. When string makes an angle 60∘ from lower vertical, acat=p. write the value of p2. (g=10m/s2)
View Solution
