An object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
75N
90N
100N
70 N
The correct Answer is:C
To solve the problem step by step, let's analyze the situation involving the mass, the string, and the forces acting on the system.
Step 1: Understand the setup
We have a mass m=10kg hanging from a massless string of length L=4m. A horizontal force F is applied at the midpoint of the string, causing the top half of the string to make an angle of 45∘ with the vertical.
Hint: Visualize the setup by drawing a diagram showing the mass, the string, and the angle formed due to the applied force.
Step 2: Analyze the forces acting on the mass
The mass experiences two forces:
1. The weight of the mass W=mg=10×9.81N=98.1N acting downward.
2. The tension T in the string acting at an angle of 45∘ with the vertical.
Hint: Remember that the tension in the string has both vertical and horizontal components.
Step 3: Resolve the tension into components
The tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
Since the angle is 45∘, we know that cos(45∘)=sin(45∘)=1√2.
Hint: Use trigonometric identities to simplify the components of tension.
Step 4: Set up the equations based on equilibrium
For vertical equilibrium:
Tcos(45∘)=mg
Substituting the values:
T(1√2)=98.1
Thus,
T=98.1√2
For horizontal equilibrium:
F=Tsin(45∘)
Substituting the value of T:
F=(98.1√2)(1√2)
This simplifies to:
F=98.1
Hint: Ensure you keep track of the units and the values used in calculations.
Step 5: Calculate the final value of F
From the calculations above, we find:
F=98.1N
Hint: Round the final answer to the nearest whole number if necessary, based on the context of the problem.
Conclusion
The magnitude of the force F applied horizontally at the midpoint of the string is approximately 98.1N, which can be rounded to 100N for practical purposes.
Final Answer: F≈100N
We have a mass m=10kg hanging from a massless string of length L=4m. A horizontal force F is applied at the midpoint of the string, causing the top half of the string to make an angle of 45∘ with the vertical.
The mass experiences two forces:
1. The weight of the mass W=mg=10×9.81N=98.1N acting downward.
2. The tension T in the string acting at an angle of 45∘ with the vertical.
The tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
For vertical equilibrium:
Tcos(45∘)=mg
Substituting the values:
T(1√2)=98.1
Thus,
T=98.1√2
F=Tsin(45∘)
Substituting the value of T:
F=(98.1√2)(1√2)
This simplifies to:
F=98.1
From the calculations above, we find:
F=98.1N
The magnitude of the force F applied horizontally at the midpoint of the string is approximately 98.1N, which can be rounded to 100N for practical purposes.
Similar Questions
A heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
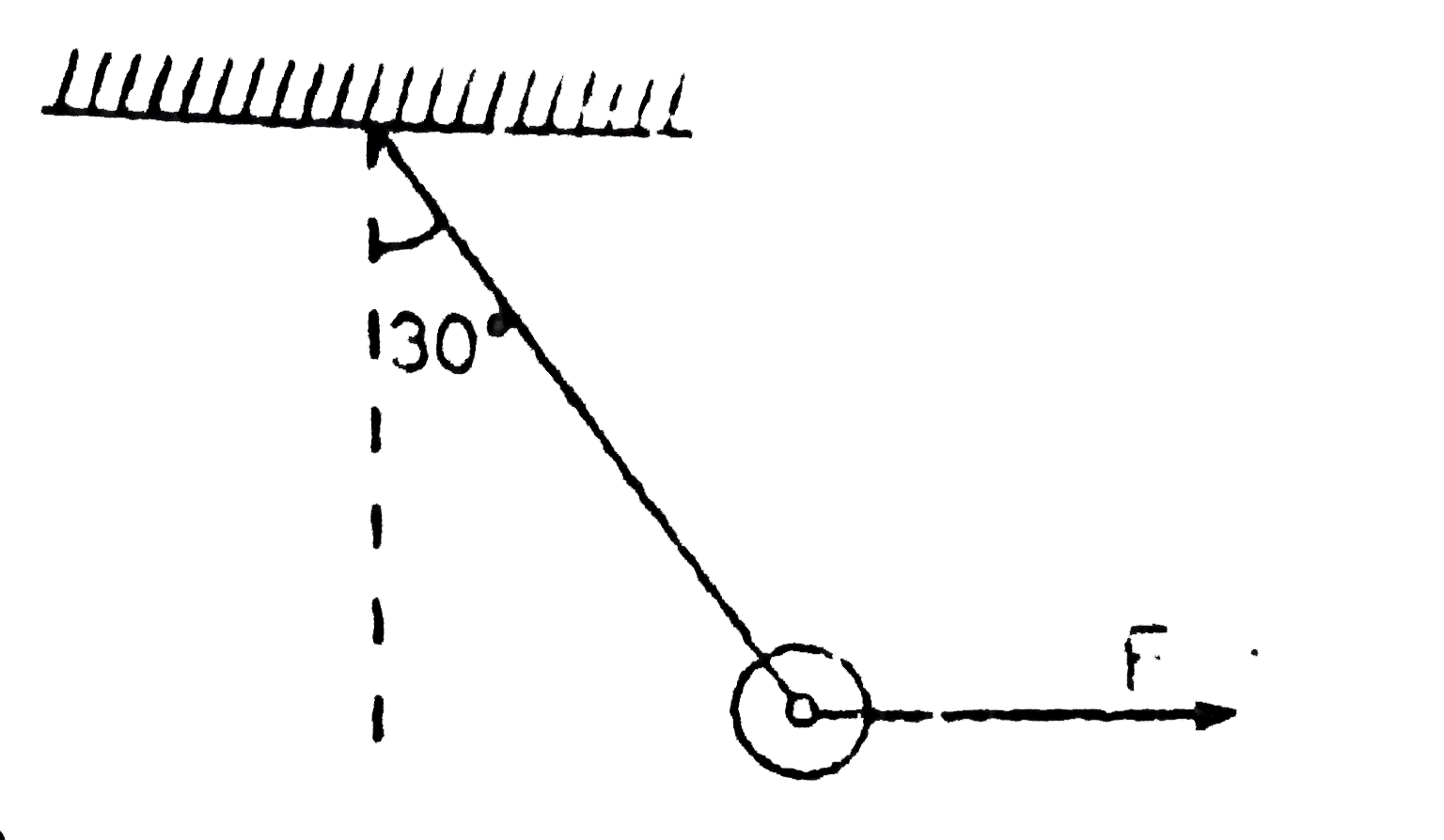 .
.
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
A block of mass 10kg is suspended from string of length 4m. When pulled by a force F along horizontal from midpoint. Upper half of string makes 45∘ with vertical, value of F is
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F
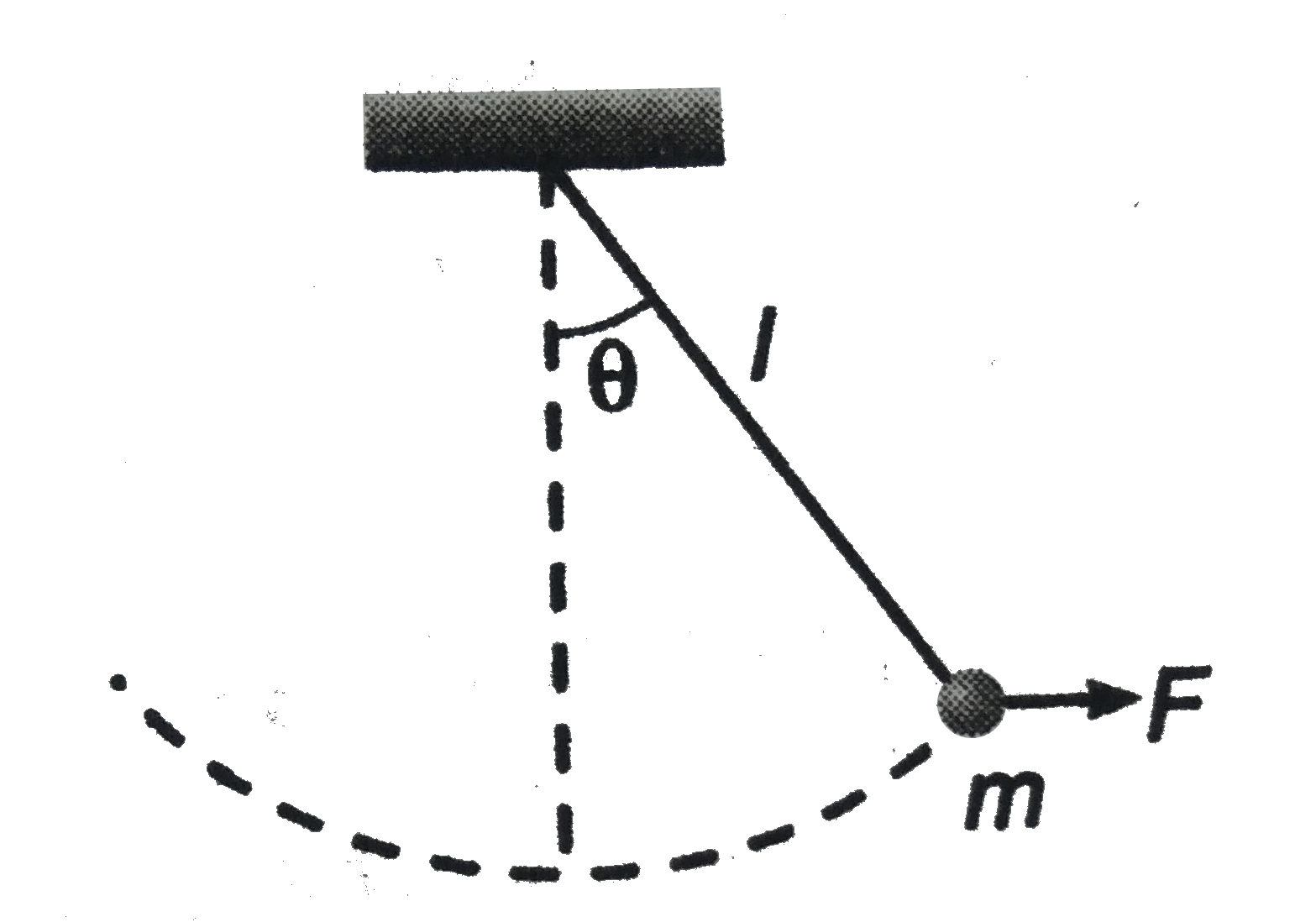 .
.
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle thit θ with the vertical. Find the work done by the force F
 .
.
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View Solution
