A solid flywheel of 20 kg mass and 120 mm radius revolves at 600revmin−1. With what force must a brake lining be pressed against it for the flywheel to stop in 3s, if the coefficient of friction is 0.1 ?
To solve the problem of how much force must be applied to the brake lining of a flywheel to stop it in a given time, we can follow these steps:
Step 1: Convert the initial angular velocity from RPM to radians per second
The initial angular velocity ω0 is given as 600 revolutions per minute (RPM). We need to convert this to radians per second.
ω0=600rev/min×2πrad1rev×1min60s=62.83rad/s
Step 2: Calculate the angular deceleration (α)
Since the flywheel comes to a stop in 3 seconds, we can use the equation of motion for angular velocity:
ω=ω0+αt
Here, ω=0 (final angular velocity), ω0=62.83rad/s, and t=3s.
Rearranging gives:
0=62.83+α⋅3⟹α=−62.833=−20.94rad/s2
Step 3: Calculate the moment of inertia (I) of the flywheel
For a solid flywheel (disk), the moment of inertia is given by:
I=12mr2
Given m=20kg and r=0.12m:
I=12×20×(0.12)2=12×20×0.0144=0.144kg m2
Step 4: Calculate the torque (τ) needed to stop the flywheel
Using the relationship between torque and angular acceleration:
τ=Iα
Substituting the values we found:
τ=0.144×(−20.94)=−3.02N m
Step 5: Relate torque to the friction force
The torque can also be expressed in terms of the friction force Ff and the radius r:
τ=Ff⋅r
The friction force is given by:
Ff=μN
Where N is the normal force (equal to the force applied F). Thus:
τ=μFr
Step 6: Solve for the applied force F
Setting the two expressions for torque equal to each other:
3.02=0.1⋅F⋅0.12
Solving for F:
F=3.020.1⋅0.12=3.020.012=251.67N
Final Answer
The force that must be applied to the brake lining to stop the flywheel in 3 seconds is approximately 251.67 N.
---
The initial angular velocity ω0 is given as 600 revolutions per minute (RPM). We need to convert this to radians per second.
Since the flywheel comes to a stop in 3 seconds, we can use the equation of motion for angular velocity:
For a solid flywheel (disk), the moment of inertia is given by:
Using the relationship between torque and angular acceleration:
The torque can also be expressed in terms of the friction force Ff and the radius r:
Setting the two expressions for torque equal to each other:
The force that must be applied to the brake lining to stop the flywheel in 3 seconds is approximately 251.67 N.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA flywheel of mass 100 kg and radius 1 m is rotating at the rate of 420 rev/min. Find the constant retarding torque to stop the wheel in 14 revolutions, the mass is concentrated at the rim. M.I. of the flywheel about its axis of rotation I=mr2.
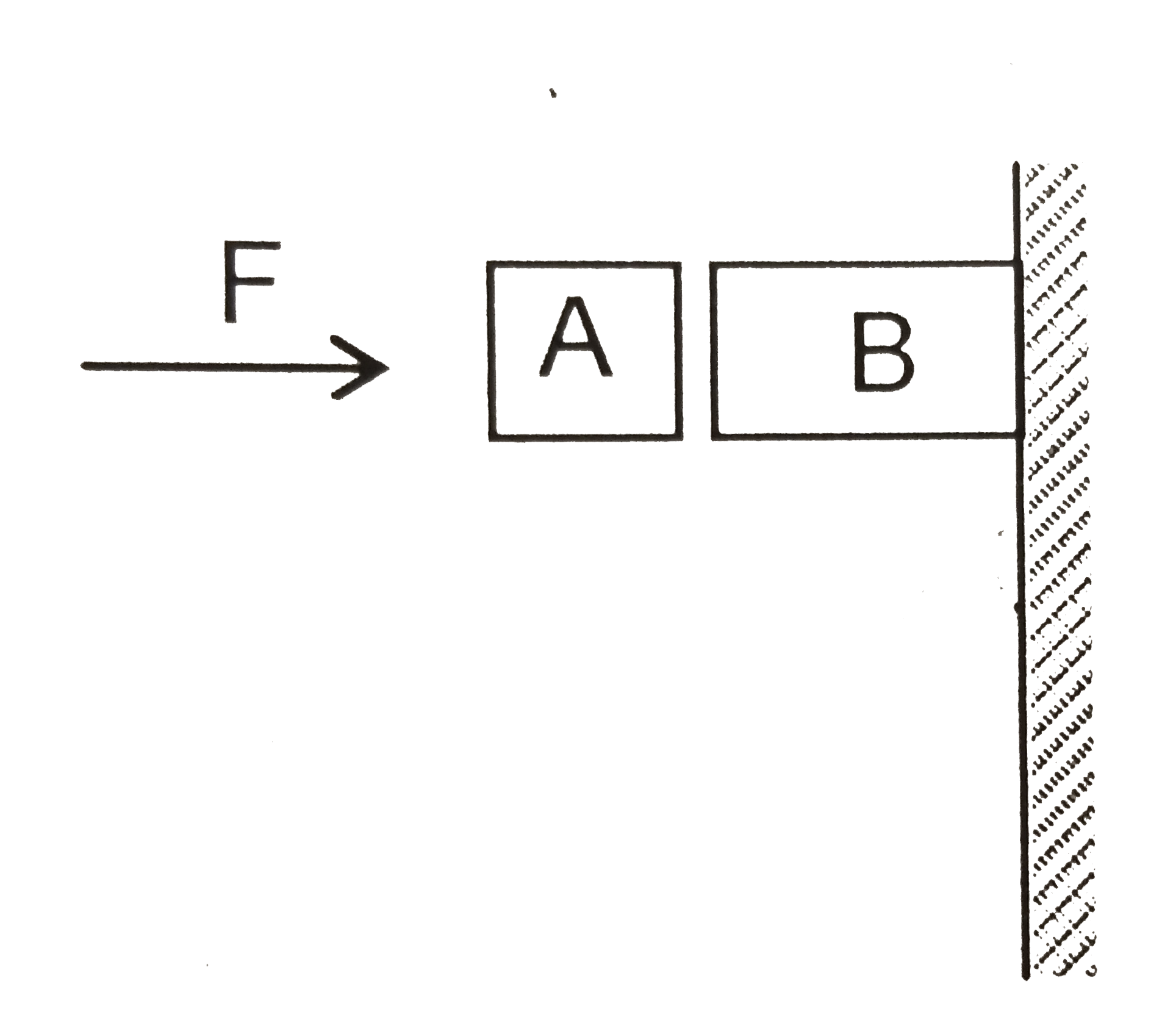
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionGiven in the figure are two blocks A and B of weight 20 N and 100 N respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is
View SolutionA solid block of mass 2kg is resting inside a cube shown in figure The cube is moving with a velocity ˆv=5ˆi+2ˆjms−1 If the coefficient of friction between the surface of cube and block is 0.2 then the force of friction between the block and cube is

View SolutionIf a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is
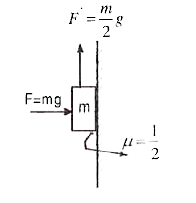
View SolutionA block of mass m is pressed against a vetical wall with a horizontal force F=mg, Anogher force F=mg/2 is acting vertically upon the block. If the coefficient of friction between the block and wall is 1/2. the force of friction between them is
View SolutionA solid cylinder wheel of mass M and radius R is pulled by a force F applied to the centre of the wheel at 37∘ to the horizontal. If the wheel is to roll without slipping, what is the maximum value of |F| ? The coefficients of static and kinetic friction are μs=0.40 and mk=0.30.(sin37∘=35)
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is rough for question, if cofficient of friction is 0.2 in both axis)
Co-ordinates of center of mass where it will stop finally are :-
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View Solution
