A particle is fired upword with a speed of 20km/s . The speed with which it will move in interstellar space is
8.8km/s
16.5km/s
4.6km/s
10km/s
The correct Answer is:B
To solve the problem of a particle fired upward with a speed of 20 km/s and to find the speed with which it will move in interstellar space, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy (kinetic + potential) at the starting point must equal the total mechanical energy at the point in interstellar space.
Step 2: Write the Initial Energy Equation
The initial kinetic energy (KE_initial) when the particle is fired is given by:
KEinitial=12mv2
where v=20km/s=20000m/s.
The initial potential energy (PE_initial) at the surface of the Earth is:
PEinitial=−GMmR
where G is the gravitational constant, M is the mass of the Earth, m is the mass of the particle, and R is the radius of the Earth.
Step 3: Write the Final Energy Equation
In interstellar space, the final potential energy (PE_final) is zero, and the final kinetic energy (KE_final) is:
KEfinal=12mv′2
where v′ is the speed in interstellar space.
Step 4: Set Up the Energy Conservation Equation
According to the conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the expressions we have:
12mv2−GMmR=12mv′2+0
Step 5: Simplify the Equation
Canceling m from all terms (assuming m≠0):
12v2−GMR=12v′2
Step 6: Rearranging the Equation
Rearranging gives:
v′2=v2−2GMR
Step 7: Calculate Escape Velocity
The escape velocity ve from the Earth is given by:
ve=√2GMR
Using the known value of escape velocity ve≈11.2km/s:
v2e=(11.2km/s)2=125.44km2/s2
Step 8: Substitute Values
Now substitute v=20km/s and v2e into the equation:
v′2=(20km/s)2−2×125.44km2/s2
v′2=400−250.88
v′2=149.12
Step 9: Calculate Final Velocity
Taking the square root gives:
v′=√149.12≈12.2km/s
Conclusion
The speed with which the particle will move in interstellar space is approximately 12.2 km/s.
The total mechanical energy (kinetic + potential) at the starting point must equal the total mechanical energy at the point in interstellar space.
The initial kinetic energy (KE_initial) when the particle is fired is given by:
KEinitial=12mv2
where v=20km/s=20000m/s.
PEinitial=−GMmR
where G is the gravitational constant, M is the mass of the Earth, m is the mass of the particle, and R is the radius of the Earth.
In interstellar space, the final potential energy (PE_final) is zero, and the final kinetic energy (KE_final) is:
KEfinal=12mv′2
where v′ is the speed in interstellar space.
According to the conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the expressions we have:
12mv2−GMmR=12mv′2+0
Canceling m from all terms (assuming m≠0):
12v2−GMR=12v′2
Rearranging gives:
v′2=v2−2GMR
The escape velocity ve from the Earth is given by:
ve=√2GMR
Using the known value of escape velocity ve≈11.2km/s:
v2e=(11.2km/s)2=125.44km2/s2
Now substitute v=20km/s and v2e into the equation:
v′2=(20km/s)2−2×125.44km2/s2
v′2=400−250.88
v′2=149.12
Taking the square root gives:
v′=√149.12≈12.2km/s
The speed with which the particle will move in interstellar space is approximately 12.2 km/s.
Topper's Solved these Questions
Similar Questions
A particle is fired vertically upward with a speed of 15kms−1. With what speed will it move in interstellar space. Assume only earth's gravitational field.
View SolutionA rocket is fired with a speed u=3√gR from the earth surface . What will be its speed at interstellar space ?
View SolutionLet escape velocity od a body a kept surface of a planet is u , If it is projected at a speed of 200 % more than the escape speed , then its speed in interstellar space will be
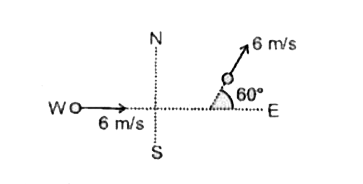
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
View SolutionA particle is fired vertically upward with a speed of 9.8kms−1. Find the maximum height attained by the particle. Radius of earth =6400 km and g at the surface=9.8ms−2. Consider only earth's gravitation.
View SolutionIf a body is thrown at speed of triple as that of escape speed (Ve) from earths surface, then at what speed it will move in interstellar space?
View Solutiontruck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
View SolutionInitial speed of an α particle inside a tube of length 4m is 1kms−1, if it is accelerated in the tube and comes out with a speed of 9kms−1 , then the time for which the particle remains inside the tube is
View SolutionAt t=0, an arrow is fired vertically upwards with a speed of 100ms−1. A second arrow is fired vertically upwads with the same speed at t=5s. Then .
View SolutionA car with a vertical windshield moves in a rain storm at a speed of 40 km/hr. The rain drops fall vertically with constant speed of 20 m/s. The angle at which rain drops strike the windshield is -
View Solution
