In elliptical orbit of a planet
angular momentum about centre of sun is constant
potential energy is constant
kinetic energy is constant
total mechanical energy is constant
The correct Answer is:A, D
To solve the question regarding the properties of a planet in an elliptical orbit around the Sun, we will analyze each option step by step.
Step 1: Analyze Angular Momentum
- Concept: Angular momentum (L) of a planet in orbit is given by the formula L=mvr, where m is the mass of the planet, v is its velocity, and r is the distance from the Sun.
- Observation: In an elliptical orbit, the net torque acting on the planet is zero because the gravitational force acts along the line connecting the planet and the Sun. Therefore, the angular momentum remains constant.
- Conclusion: The first option, "angular momentum about the center of the Sun is constant," is correct.
Step 2: Analyze Potential Energy
- Concept: The gravitational potential energy (U) between two masses is given by U=−Gm1m2r, where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between them.
- Observation: As the planet moves in its elliptical orbit, the distance r between the planet and the Sun changes. Since potential energy is inversely proportional to r, it varies as the distance changes.
- Conclusion: The second option, "potential energy is constant," is incorrect.
Step 3: Analyze Kinetic Energy
- Concept: The kinetic energy (K) of the planet is given by K=12mv2.
- Observation: In an elliptical orbit, the speed of the planet varies; it moves faster when closer to the Sun (periapsis) and slower when farther away (apoapsis). Thus, the kinetic energy also changes as the speed changes.
- Conclusion: The third option, "kinetic energy is constant," is incorrect.
Step 4: Analyze Total Mechanical Energy
- Concept: The total mechanical energy (E) of the system is the sum of kinetic and potential energy, E=K+U.
- Observation: In an isolated system (like the planet-Sun system), the total mechanical energy remains constant over time, even though kinetic and potential energy may change individually.
- Conclusion: The fourth option, "total mechanical energy is constant," is correct.
Final Summary of Correct Options
- The correct options are:
- A: Angular momentum about the center of the Sun is constant (Correct)
- B: Potential energy is constant (Incorrect)
- C: Kinetic energy is constant (Incorrect)
- D: Total mechanical energy is constant (Correct)
- Concept: Angular momentum (L) of a planet in orbit is given by the formula L=mvr, where m is the mass of the planet, v is its velocity, and r is the distance from the Sun.
- Observation: In an elliptical orbit, the net torque acting on the planet is zero because the gravitational force acts along the line connecting the planet and the Sun. Therefore, the angular momentum remains constant.
- Conclusion: The first option, "angular momentum about the center of the Sun is constant," is correct.
- Concept: The gravitational potential energy (U) between two masses is given by U=−Gm1m2r, where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between them.
- Observation: As the planet moves in its elliptical orbit, the distance r between the planet and the Sun changes. Since potential energy is inversely proportional to r, it varies as the distance changes.
- Conclusion: The second option, "potential energy is constant," is incorrect.
- Concept: The kinetic energy (K) of the planet is given by K=12mv2.
- Observation: In an elliptical orbit, the speed of the planet varies; it moves faster when closer to the Sun (periapsis) and slower when farther away (apoapsis). Thus, the kinetic energy also changes as the speed changes.
- Conclusion: The third option, "kinetic energy is constant," is incorrect.
- Concept: The total mechanical energy (E) of the system is the sum of kinetic and potential energy, E=K+U.
- Observation: In an isolated system (like the planet-Sun system), the total mechanical energy remains constant over time, even though kinetic and potential energy may change individually.
- Conclusion: The fourth option, "total mechanical energy is constant," is correct.
- The correct options are:
- A: Angular momentum about the center of the Sun is constant (Correct)
- B: Potential energy is constant (Incorrect)
- C: Kinetic energy is constant (Incorrect)
- D: Total mechanical energy is constant (Correct)
Topper's Solved these Questions
Similar Questions
_S01_025_Q01.png)
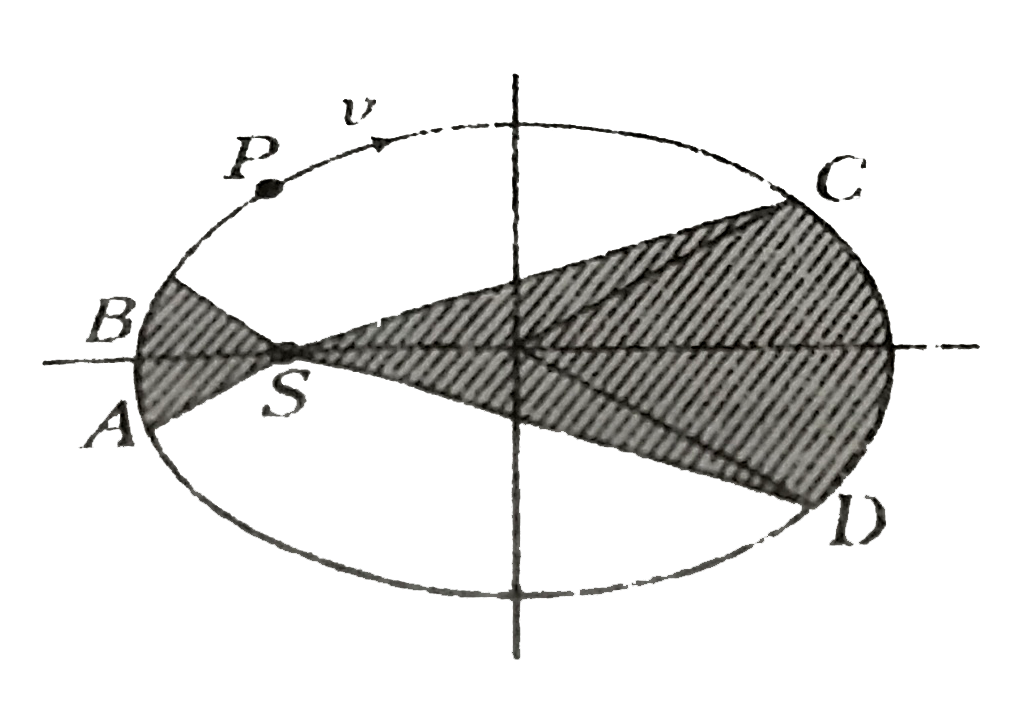
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:
View SolutionThe figure shows elliptical orbit of a plant P about the sun S. The shaded area CSD is twice tha shaded area ASB. If t1 is the time taken by the planet to move from C to D and t2 is the time to move from A to B, determine the ratio t1/t2
View Solution
Knowledge Check
_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:At1=t2Bt1=2t2Ct1=4t2Dt1>t2
The figure represents an elliptical orbit a planet around sun. The planet takes time T1 to travel from A to B and it takes time T2 to travel from C to D. If the area CSD is double that of area ASB, them

View Solution_E01_028_Q01.png)
Spacemen Fred's spaceship (which has negligible mass) is in an elliptical orbit about planet Bob. The minimum distance between the spaceship and the planet is R, the maximum distance between the spaceship and the planet is 2R. At the point of maximum distance, spaceman fred is traveling at speed v0. he then fires his thrusters so that he enters a circular orbit of radius 2R. what is his new speed?
View SolutionA satellite with mass 2000 kg and angular momentum magnitude 2×1012kg.m2/s is moving in an elliptical orbit around a plate. The rate at which area is swept out by the satellite around the planet, is equal to
View SolutionA satellite is in an elliptical orbit around a planet P. It is observed that the velocity of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet . The ratio of distances between the statellite and the planet at closest and farthest points is :
View SolutionWhen a satellite has an elliptical orbit the plane of the orbit
View SolutionThe given figure shows several possible elliptical orbits of a satellite . Then match the following.

View SolutionThe given figure shows several possible elliptical orbits of a satellite. On which orbit will the satellite acquire the largest speed ?
View Solution
