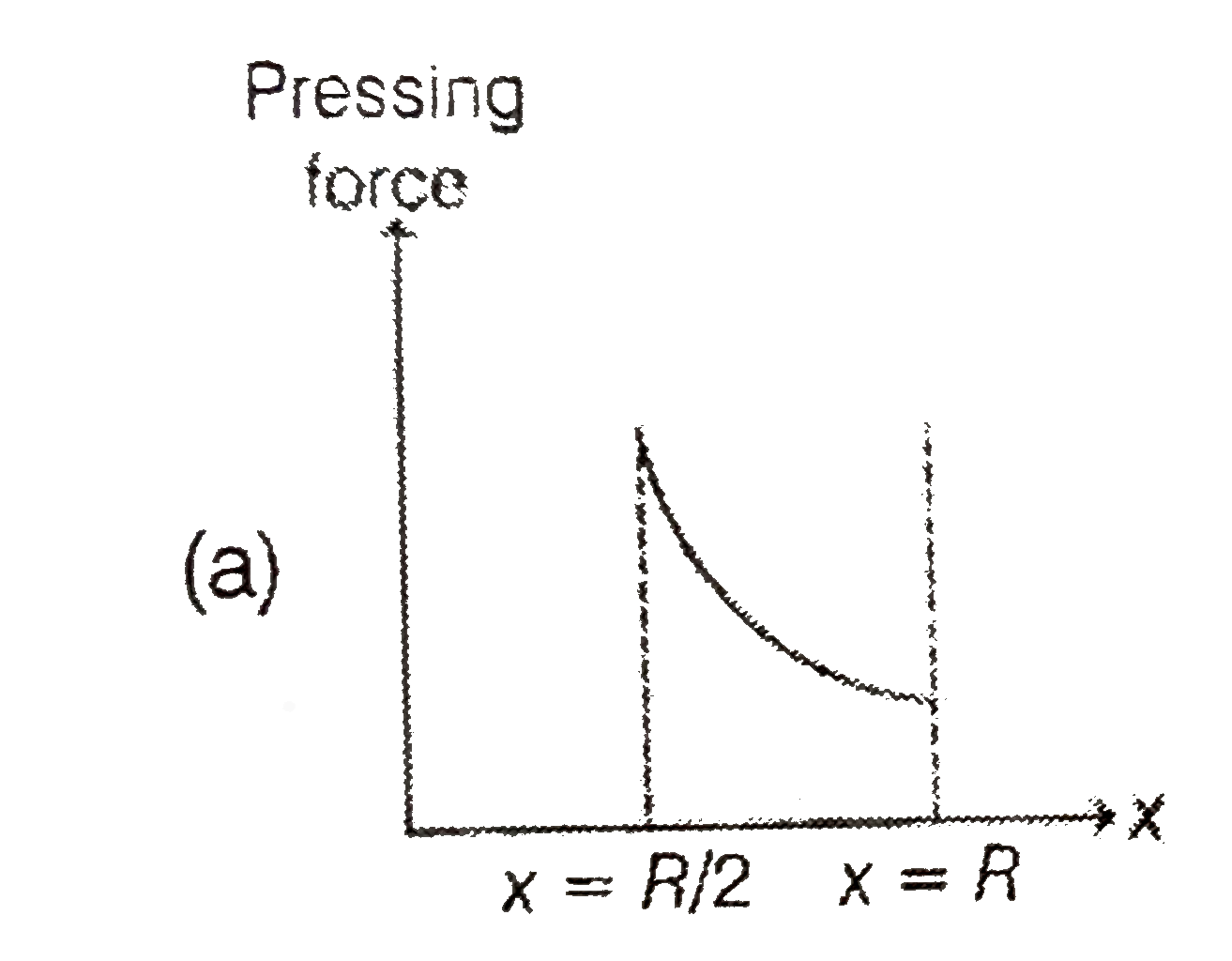
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to


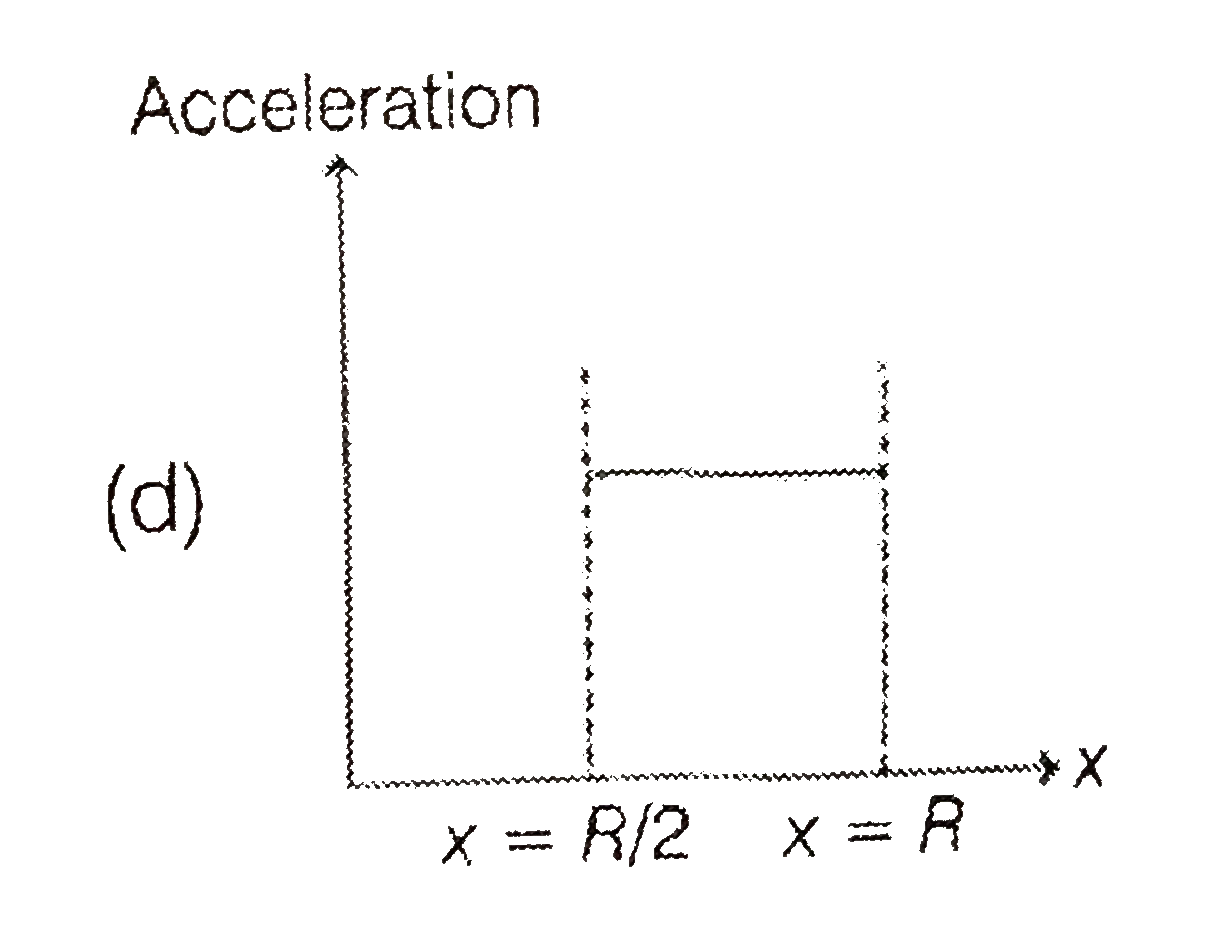
The correct Answer is:B, C
To solve the problem of a particle released from one end of a tunnel dug along a chord of the Earth at a perpendicular distance R/2 from the Earth's center, we will analyze the forces acting on the particle and derive the expressions for the pressing force on the wall and the acceleration of the particle.
1. Understanding the Setup:
- The tunnel is dug along a chord of the Earth, and the distance from the center of the Earth to the tunnel is R/2.
- A particle is released from one end of the tunnel.
2. Determine the Gravitational Force:
- The gravitational force acting on the particle at a distance x from the center of the Earth can be given by:
g′=g(1−xR)
- Here, g is the acceleration due to gravity at the surface of the Earth.
3. Finding the Normal Force (Pressing Force):
- The normal force N acting on the particle due to the wall of the tunnel can be expressed as:
N=mg′sin(θ)
- The angle θ can be determined using the geometry of the situation. Since the tunnel is at a distance R/2, we can find sin(θ) in terms of x:
sin(θ)=R/2x
- Substituting g′ into the normal force equation gives:
N=mg(1−xR)⋅R/2x
4. Simplifying the Normal Force:
- Rearranging the equation yields:
N=mgR2(1x−1R)
- This shows that the normal force varies inversely with x.
5. Finding the Acceleration of the Particle:
- The net force acting on the particle is given by:
F=mg′cos(θ)
- The acceleration a can then be expressed as:
a=Fm=g′cos(θ)
- Substituting g′ and cos(θ) gives:
a=g(1−xR)⋅√R2−(R/2)2x
- Simplifying this expression shows that the acceleration varies quadratically with x.
6. Conclusion:
- The pressing force N varies inversely with x, and the acceleration a varies quadratically with x.
- Based on the analysis, we can conclude that the correct options for the graphs of pressing force and acceleration are as follows:
- The pressing force N is constant with respect to x.
- The acceleration a is a parabolic function of x.
- The tunnel is dug along a chord of the Earth, and the distance from the center of the Earth to the tunnel is R/2.
- A particle is released from one end of the tunnel.
- The gravitational force acting on the particle at a distance x from the center of the Earth can be given by:
g′=g(1−xR)
- Here, g is the acceleration due to gravity at the surface of the Earth.
- The normal force N acting on the particle due to the wall of the tunnel can be expressed as:
N=mg′sin(θ)
- The angle θ can be determined using the geometry of the situation. Since the tunnel is at a distance R/2, we can find sin(θ) in terms of x:
sin(θ)=R/2x
- Substituting g′ into the normal force equation gives:
N=mg(1−xR)⋅R/2x
- Rearranging the equation yields:
N=mgR2(1x−1R)
- This shows that the normal force varies inversely with x.
- The net force acting on the particle is given by:
F=mg′cos(θ)
- The acceleration a can then be expressed as:
a=Fm=g′cos(θ)
- Substituting g′ and cos(θ) gives:
a=g(1−xR)⋅√R2−(R/2)2x
- Simplifying this expression shows that the acceleration varies quadratically with x.
- The pressing force N varies inversely with x, and the acceleration a varies quadratically with x.
- Based on the analysis, we can conclude that the correct options for the graphs of pressing force and acceleration are as follows:
- The pressing force N is constant with respect to x.
- The acceleration a is a parabolic function of x.
Topper's Solved these Questions
Similar Questions
A tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
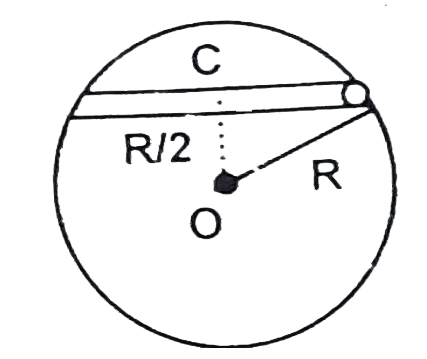
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionThe distance of the centres of moon the earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth, the gravitational force on a particle will be zero.
View SolutionA tuning is dug along the diameter of the earth. There is particle of mass m at the centre of the tunel. Find the minimum velocity given to the particle so that is just reaches to the surface of the earth. (R= radius of earth)
View Solution
