The current in ampere through an inductor is
i=(20t+10)
Here t is in second. The induced emf in the inductor 4V.
Total flux linked with the inductor at t= 2 is a
10 Wb
20 Wb
30 Wb
40 Wb
The correct Answer is:A
To solve the problem, we need to find the total flux linked with the inductor at t=2 seconds given the current i(t)=20t+10 and the induced emf E=4 volts.
1. Identify the given information:
- Current through the inductor: i(t)=20t+10
- Induced emf: E=4 volts
2. Use the formula for induced emf:
The induced emf in an inductor is given by the formula:
E=Ldidt
where L is the inductance and didt is the rate of change of current with respect to time.
3. Differentiate the current with respect to time:
We need to find didt:
i(t)=20t+10
Differentiating:
didt=20
4. Substitute into the emf formula:
Now substitute didt into the induced emf equation:
4=L⋅20
5. Solve for inductance L:
Rearranging the equation gives:
L=420=15 Henry
6. Calculate the current at t=2 seconds:
Substitute t=2 into the current equation:
i(2)=20(2)+10=40+10=50 A
7. Calculate the total flux Φ:
The total flux linked with the inductor is given by:
Φ=L⋅i
Substitute the values of L and i:
Φ=15⋅50=10 Weber
Final Answer:
The total flux linked with the inductor at t=2 seconds is 10 Weber.
- Current through the inductor: i(t)=20t+10
- Induced emf: E=4 volts
The induced emf in an inductor is given by the formula:
E=Ldidt
where L is the inductance and didt is the rate of change of current with respect to time.
We need to find didt:
i(t)=20t+10
Differentiating:
didt=20
Now substitute didt into the induced emf equation:
4=L⋅20
Rearranging the equation gives:
L=420=15 Henry
Substitute t=2 into the current equation:
i(2)=20(2)+10=40+10=50 A
The total flux linked with the inductor is given by:
Φ=L⋅i
Substitute the values of L and i:
Φ=15⋅50=10 Weber
The total flux linked with the inductor at t=2 seconds is 10 Weber.
Similar Questions
The current in ampere through an inductor is
i=(10+20t)
Here t is in second. The induced emf in the inductor 4V.
The self inductance of the indicator is, L…..H,
View SolutionThe current (in Ampere) in an inductor is given by l=5+16t, where t in seconds. The selft - induced emf in it is 10mV. Find
(a) the self-inductance, and
(b) the energy stored in the inductor and the power supplied to it at t=1s
View SolutionIf the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionThe magnetic flux through each turn of a 100 turn coil is (t3–2t)×10−3Wb, where t is in second. The induced emf at t = 2 s is
View SolutionThe current through inductor of 2H is given by I=2tcos2t. The voltage across the inductor is
View SolutionThe current in a 90mH inductor changes with time as i=1.0t2−6t, where I is in amperes and t is in seconds.
View SolutionThe current through a 4.6 H inductor is shown in the following graph. The induced emf during the time interval t = 5 milli - sec to 6 milli - sec will be
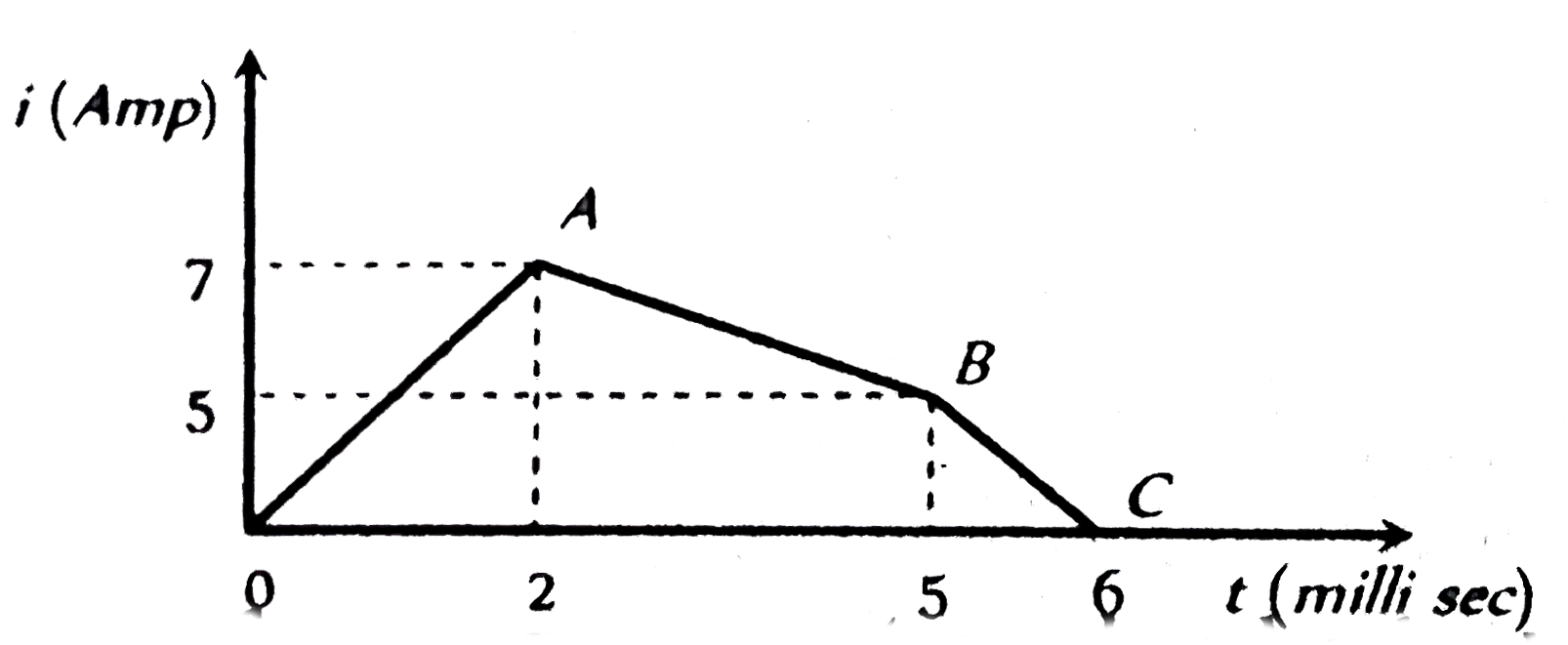
View SolutionIn an inductor, the current / varies with time to l=5A+16.(A/s)t. If-induced emf in the induct is 5 mV, the self inductance of the inductor is
View Solution
