Two parallel long straight conductors lie on a smooth horizontal surface. Two other parallel conductor rest on them at right angles so as from B exits vertical. A uniform magnetic field B exists a vertical direction. Now all the four conductors stock moving outwards with a constant velocity v. The induced emf e and induced current i will vary wide time t as


The correct Answer is:A, D
To solve the problem, we need to analyze the situation involving the four conductors, the magnetic field, and the motion of the conductors. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have two long straight conductors lying horizontally and two other conductors resting on them at right angles. A uniform magnetic field B is directed vertically, and all four conductors are moving outward with a constant velocity v.
Step 2: Determine the Change in Area
Initially, let the side length of the area formed by the conductors be a. As the conductors move outward, the distance between them increases. After a time t, each conductor moves a distance vt. Therefore, the new side length a′ becomes:
a′=a+2vt
The area A at any time t is given by:
A=(a+2vt)2
Step 3: Calculate the Rate of Change of Area
To find the induced EMF, we need to calculate the rate of change of area with respect to time:
dAdt=ddt((a+2vt)2)=2(a+2vt)⋅ddt(a+2vt)=2(a+2vt)⋅2v=4v(a+2vt)
Step 4: Calculate the Rate of Change of Magnetic Flux
The magnetic flux Φ through the area is given by:
Φ=B⋅A
Thus, the rate of change of magnetic flux is:
dΦdt=B⋅dAdt=B⋅4v(a+2vt)
Step 5: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF e is equal to the negative rate of change of magnetic flux:
e=−dΦdt=−B⋅4v(a+2vt)
Since we are interested in the magnitude, we can ignore the negative sign:
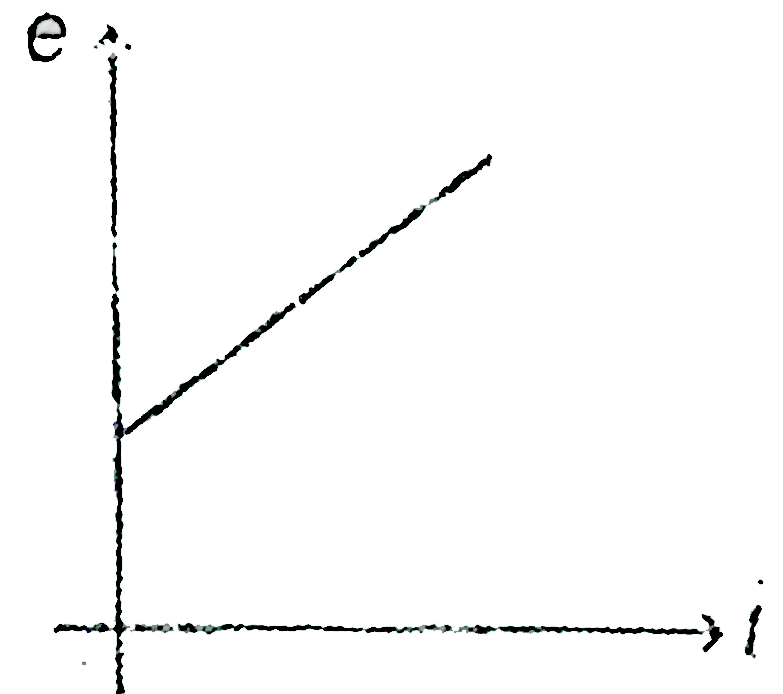
e=4Bv(a+2vt)
Step 6: Calculate the Induced Current
The resistance R of the conductors can be expressed in terms of their resistance per unit length r and the total length of the conductors. The total resistance R at any time is:
R=r⋅(4(a+2vt))
Thus, the induced current i can be calculated using Ohm's law i=eR:
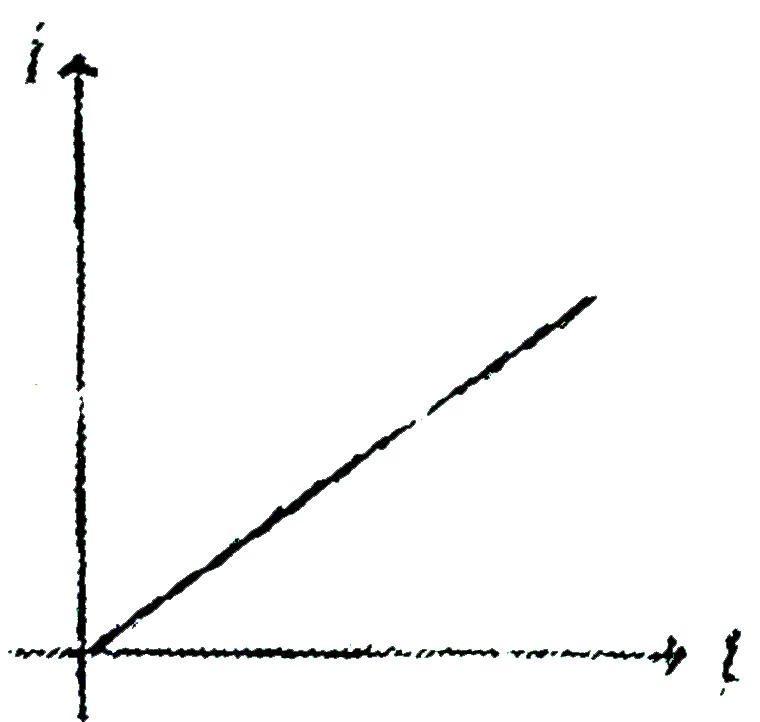
i=4Bv(a+2vt)r⋅(4(a+2vt))=Bvr
This shows that the induced current i is constant over time since it does not depend on t.
Conclusion
- The induced EMF e increases with time as e=4Bv(a+2vt).
- The induced current i remains constant as i=Bvr.
We have two long straight conductors lying horizontally and two other conductors resting on them at right angles. A uniform magnetic field B is directed vertically, and all four conductors are moving outward with a constant velocity v.
Initially, let the side length of the area formed by the conductors be a. As the conductors move outward, the distance between them increases. After a time t, each conductor moves a distance vt. Therefore, the new side length a′ becomes:
a′=a+2vt
The area A at any time t is given by:
A=(a+2vt)2
To find the induced EMF, we need to calculate the rate of change of area with respect to time:
dAdt=ddt((a+2vt)2)=2(a+2vt)⋅ddt(a+2vt)=2(a+2vt)⋅2v=4v(a+2vt)
The magnetic flux Φ through the area is given by:
Φ=B⋅A
Thus, the rate of change of magnetic flux is:
dΦdt=B⋅dAdt=B⋅4v(a+2vt)
According to Faraday's law of electromagnetic induction, the induced EMF e is equal to the negative rate of change of magnetic flux:
e=−dΦdt=−B⋅4v(a+2vt)
Since we are interested in the magnitude, we can ignore the negative sign:
e=4Bv(a+2vt)
The resistance R of the conductors can be expressed in terms of their resistance per unit length r and the total length of the conductors. The total resistance R at any time is:
R=r⋅(4(a+2vt))
Thus, the induced current i can be calculated using Ohm's law i=eR:
i=4Bv(a+2vt)r⋅(4(a+2vt))=Bvr
This shows that the induced current i is constant over time since it does not depend on t.
- The induced EMF e increases with time as e=4Bv(a+2vt).
- The induced current i remains constant as i=Bvr.
Similar Questions
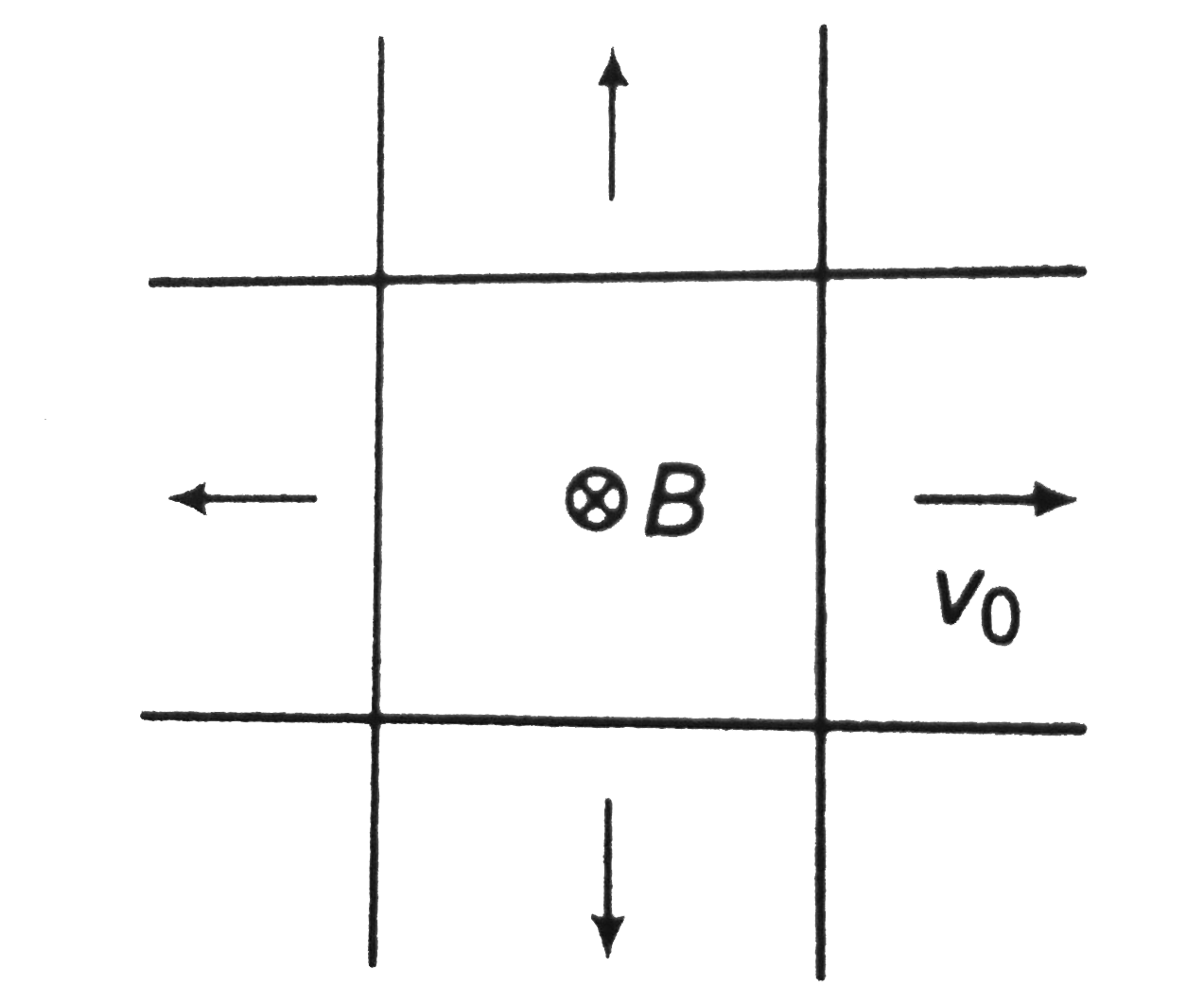
Two parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward witha constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
View SolutionTwo parallel, long, straight conductor lie on a smooth plane surface. Two other parallel so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the cinductors. Now they start moving out with a constant velocity v.
(A) Will the induced emf be time dependent?
(b) Will the current be time dependent ?
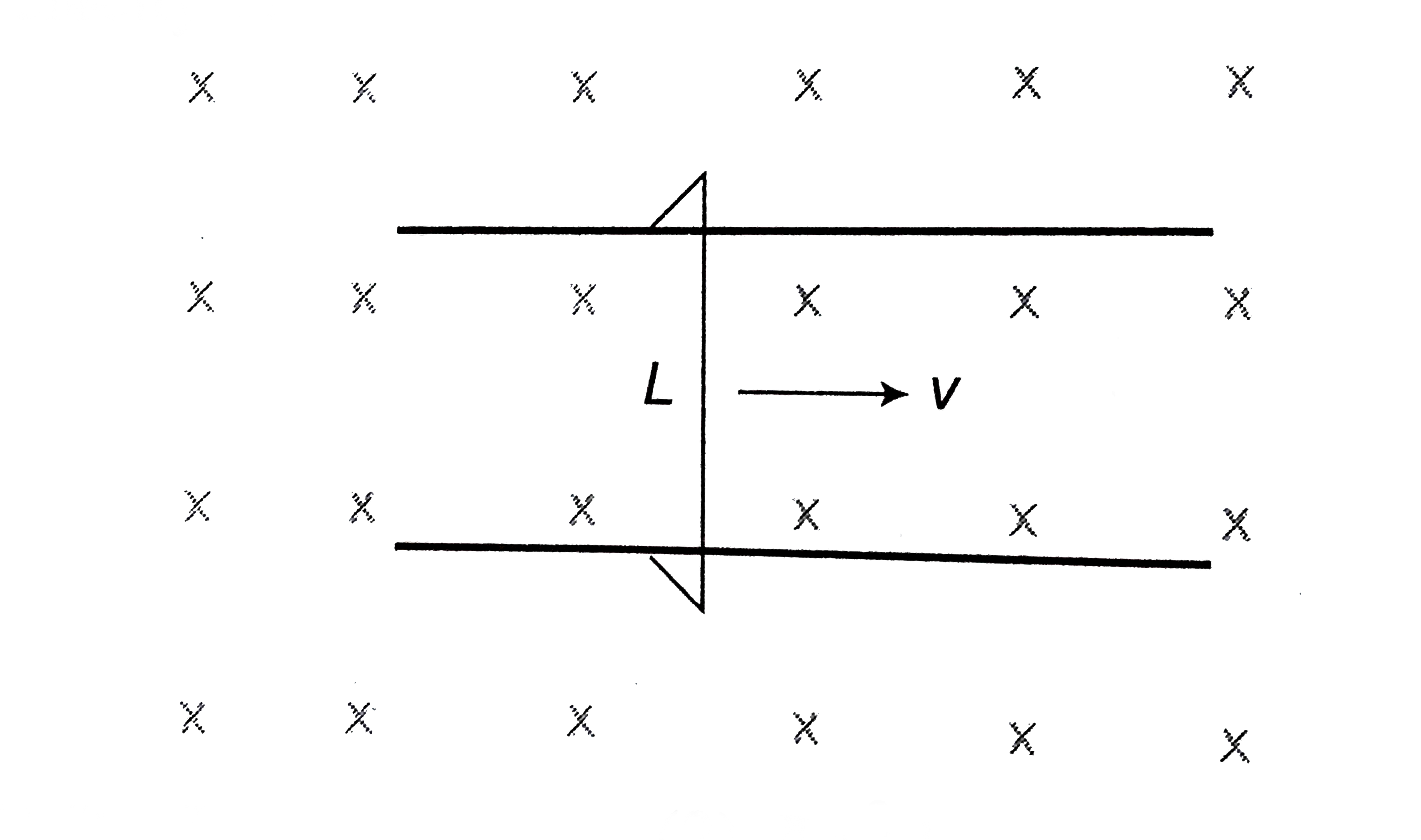
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
View SolutionA square loop of edge a having n turns Is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position . A uniform magnetic field B exists in the vertical direction. Find the emf induced in the coil.

View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionTwo parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are λ no other wire has resistance. Then :

View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
View SolutionA loop is formed by two parallel conductors connected by a selenoid with inductance L and a condutcing rod of mass which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in as uniform vertical magnetic field B.The distance between the conductors is l.

At the moment t=0 the rod is impart the initial velocity v0 directed to the right. find the equation of its motion d(t) if the electric resistance of the loop is negligible
View SolutionA square loop of edge b having M turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B0 exists in the vertical direction.
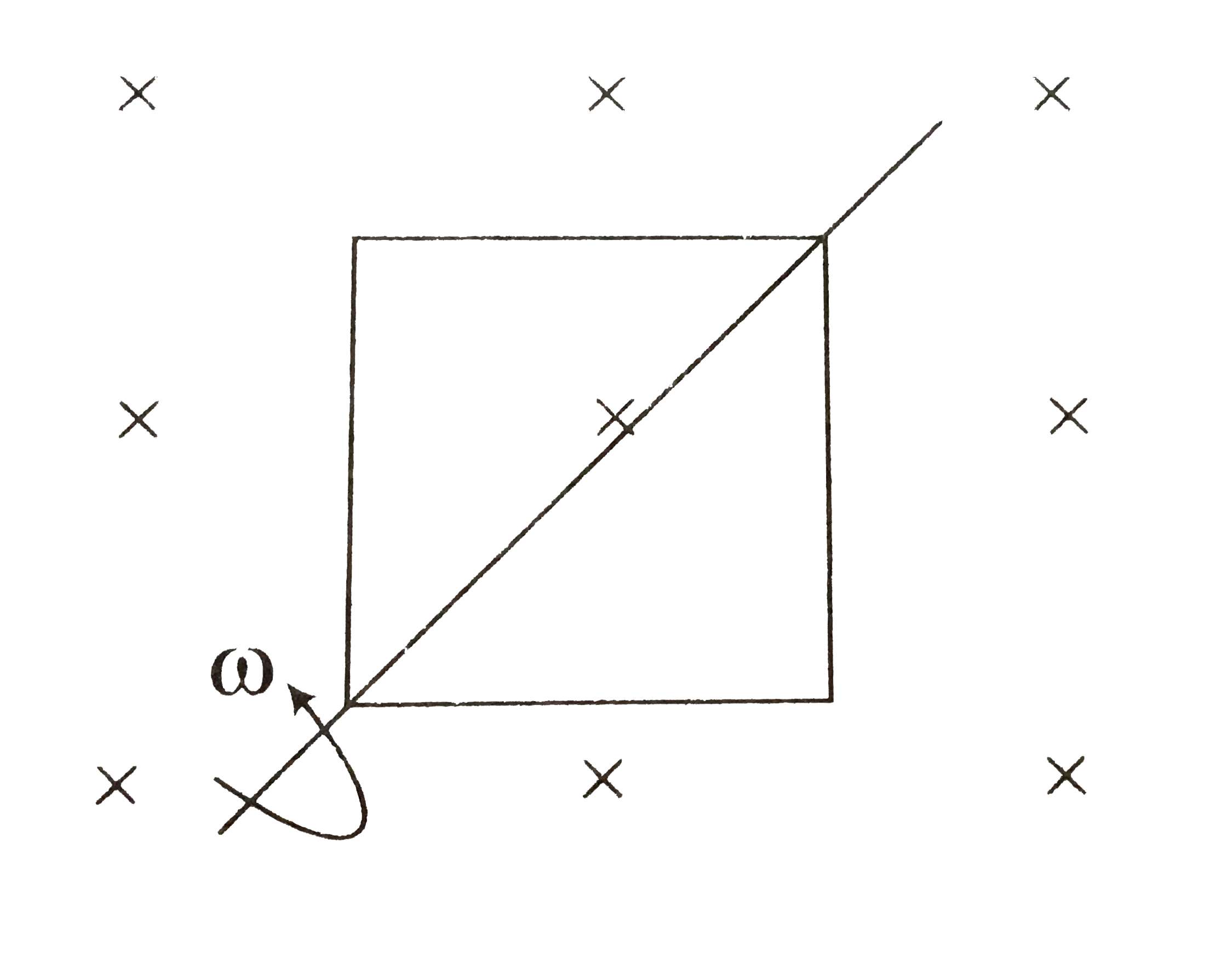
Find (i) the emf induced in the coil as a function of time t.
(ii) the maximum emf induced.
(iii) the average emf induced in the loop over a long period.
(iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T.
(v) heat produced in time t = 0 to t = 2T.
View Solution
