A loop is formed by two parallel conductors connected by a selenoid with inductance L and a condutcing rod of mass which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in as uniform vertical magnetic field B.The distance between the conductors is l.

At the moment t=0 the rod is impart the initial velocity v0 directed to the right. find the equation of its motion d(t) if the electric resistance of the loop is negligible
Let at any instant of time velocity of the rod is v towards right. The current in the circuit is i. In the figure.
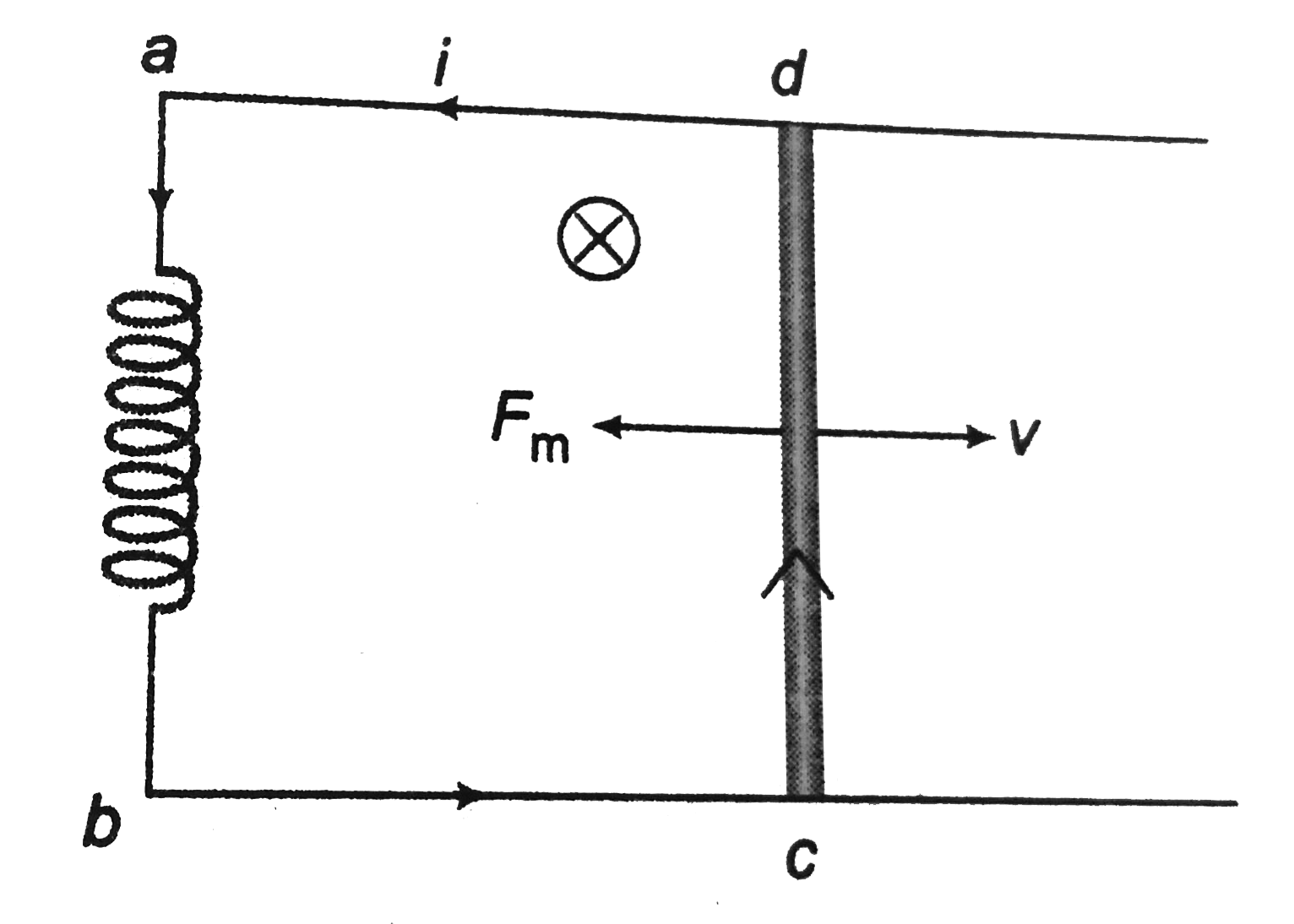
Va−Vb=Vd−Vc
or L=didt=Bvl=Bldxdt ( as v=dxdt)
i.e., Ldi=Bldx
Integrating on both side we get
Li=Blx
or i=BlLx..........i
Magnetic fore on the rod at this instant is
Fm=ilB=B2l2Lx............ii
Since, this force is in opposite direction of v, so from newton's second law we can write
m(d2xdt2)=−B2l2Lx
or (d2xdt2)=−B2l2mLx
comparing this with equation of SHM,
dxdt2=−ω2x
We have ω=Bl√mL
Therefore, the rod will oscillate simple harmonically with angular frequency ω=Bl√mL. At time t=0, rod was at x=0 and it was moving towards positive x-axis.Hence x−t equation of the rod is
x=Asinωt.........iii
To find A , we use the fact that at t=0,v or dxdt has a value v0. Hence,
dxdt=v=Aωcosωt
or Aω=v0(at t=0)
or A=v0ω
substitutng in Eqn iii we have
x=v0ωsinωt, where ω=Bl√mL
At x=A,v=0 i.e. whole of its kinetic energy is converted into magnetic energy. Thus,
12Li2=12mv20
Substituting value of i from Eq. (i), with x=A, we have
L(BlLA)2=mv20
or A=√mLBlv0=v0ω
as ω=Bl√mL
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.18videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 52videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A loop is formed by two parallel conductors connected by a solenoid with inductance L=2H and a conducting rod of mass m=80g, which can freely (without fricition) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B=4T.
The distance between the conductors is equal to l=4cm. At the moment t=0 the rod is imparted an initial velocity v0=2cm/s directed to the right. Find the amplitude (in cm) for the oscillations of conducting rod, if the electric resistance of the loop is negligible.
 View Solution
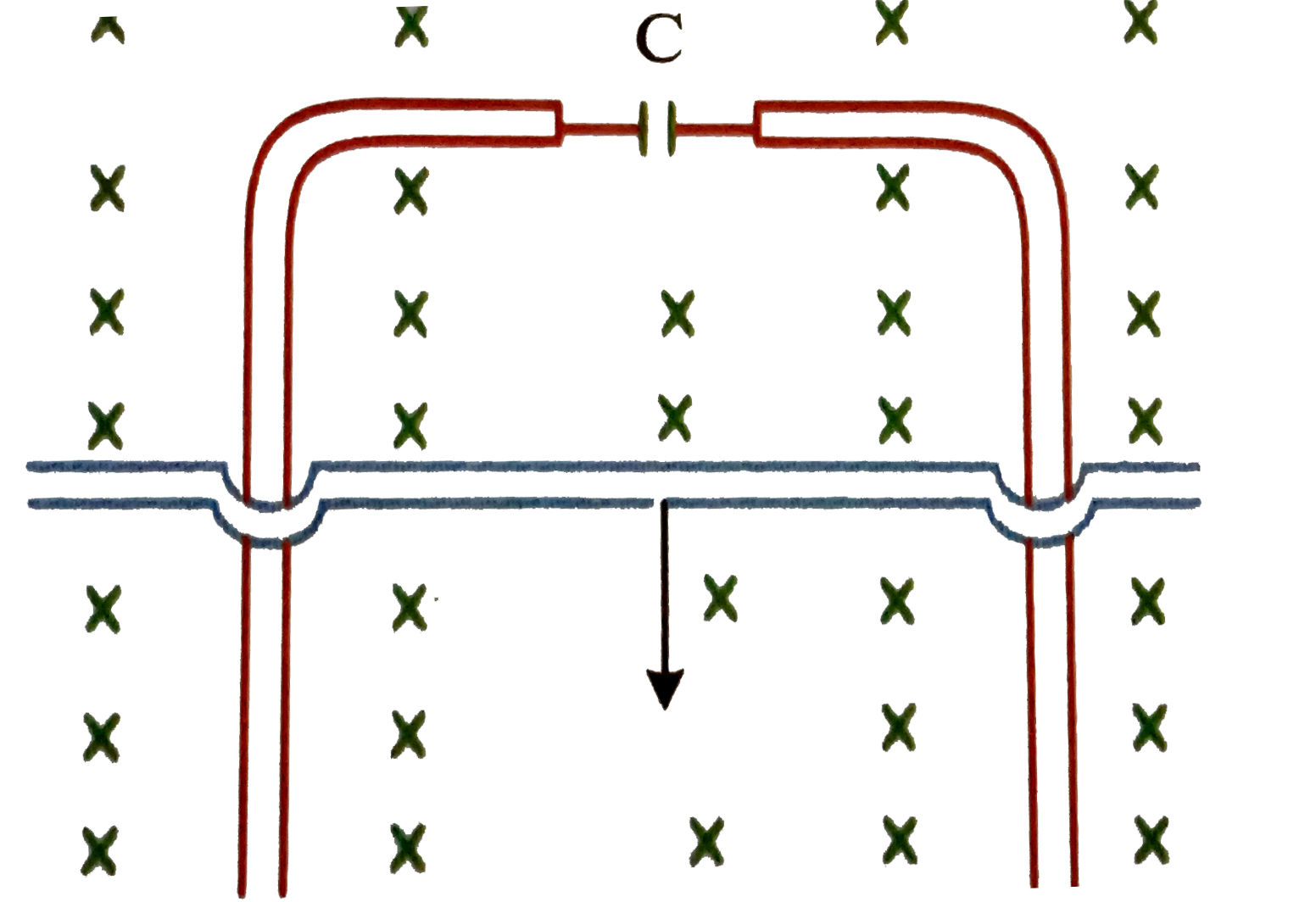
View SolutionA conductor of length l and mass m can slide without any friction along the two vertical conductors connected at the top through a capacitor. A uniform magnetic field B is set up ⊥ to the plane of paper. The acceleration of the conductor
 View Solution
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
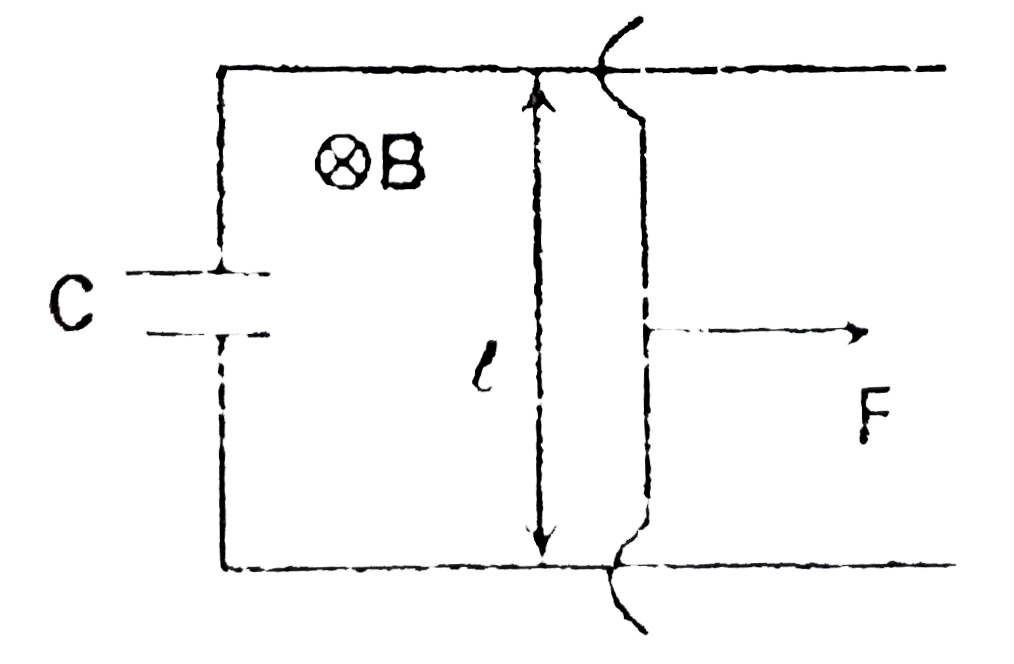
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
 View Solution
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionA conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
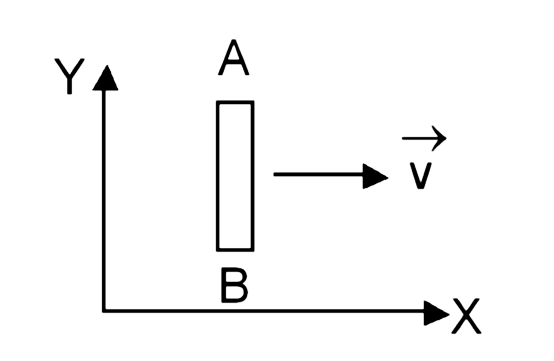
View SolutionA conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
 View Solution
View SolutionTwo identical conductors P and Q are placed on two friction less rails R and S in a uniform magnetic field directed into the plane. If P is moved in the direction shown in figure with a constant speed, then rod Q
 View Solution
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then
 View Solution
View Solution

