In L-C-R series circuit suppose ωr is resonance frequency, then match the following table,
Table-1Table-2(A)If ω>ωr(P)Current will lead the voltage(B)If ω=ωr(Q)Voltage will lead the current(C)If ω=2ωr(R)XL=2XC(D)If ω<ωr(S)Current and voltage are in phase(T)None
The correct Answer is:(A) Q, (B) S, (C) Q, (D) P
To solve the problem of matching the conditions of an L-C-R series circuit at different frequencies with their corresponding behaviors, we can follow these steps:
Step 1: Understanding Resonance Frequency
The resonance frequency, denoted as ωr, is the frequency at which the inductive reactance XL equals the capacitive reactance XC. At this frequency, the circuit behaves purely resistively.
Step 2: Analyzing the Cases
We will analyze the behavior of the circuit under the following conditions:
1. ω>ωr
2. ω=ωr
3. ω<ωr
4. ω=2ωr
Step 3: Matching Conditions with Behaviors
Case A: ω>ωr
- The circuit becomes inductive.
- In an inductive circuit, the voltage leads the current.
- Therefore, A matches with Q.
Case B: ω=ωr
- The circuit is at resonance.
- At resonance, the current and voltage are in phase.
- Therefore, B matches with S.
Case C: ω=2ωr
- This condition is also greater than ωr, so the circuit remains inductive.
- Again, in an inductive circuit, the voltage leads the current.
- Therefore, C matches with Q.
Case D: ω<ωr
- The circuit becomes capacitive.
- In a capacitive circuit, the current leads the voltage.
- Therefore, D matches with P.
Summary of Matches
- A → Q (If ω>ωr, Voltage leads Current)
- B → S (If ω=ωr, Current and Voltage are in phase)
- C → Q (If ω=2ωr, Voltage leads Current)
- D → P (If ω<ωr, Current leads Voltage)
Final Matching Table
- A → Q
- B → S
- C → Q
- D → P
The resonance frequency, denoted as ωr, is the frequency at which the inductive reactance XL equals the capacitive reactance XC. At this frequency, the circuit behaves purely resistively.
We will analyze the behavior of the circuit under the following conditions:
1. ω>ωr
2. ω=ωr
3. ω<ωr
4. ω=2ωr
- The circuit becomes inductive.
- In an inductive circuit, the voltage leads the current.
- Therefore, A matches with Q.
- The circuit is at resonance.
- At resonance, the current and voltage are in phase.
- Therefore, B matches with S.
- This condition is also greater than ωr, so the circuit remains inductive.
- Again, in an inductive circuit, the voltage leads the current.
- Therefore, C matches with Q.
- The circuit becomes capacitive.
- In a capacitive circuit, the current leads the voltage.
- Therefore, D matches with P.
- A → Q (If ω>ωr, Voltage leads Current)
- B → S (If ω=ωr, Current and Voltage are in phase)
- C → Q (If ω=2ωr, Voltage leads Current)
- D → P (If ω<ωr, Current leads Voltage)
- A → Q
- B → S
- C → Q
- D → P
Similar Questions
During current growth in L-R circuit, match the following table,

View SolutionAngular frequency ω in an AC, L-C-R series circuit is gradually increased. Then, match the following two columns.

View SolutionIn an AC, series L-C-R circuit, R=XL=XC and applied AC, voltage is V. Then match the following two columns.
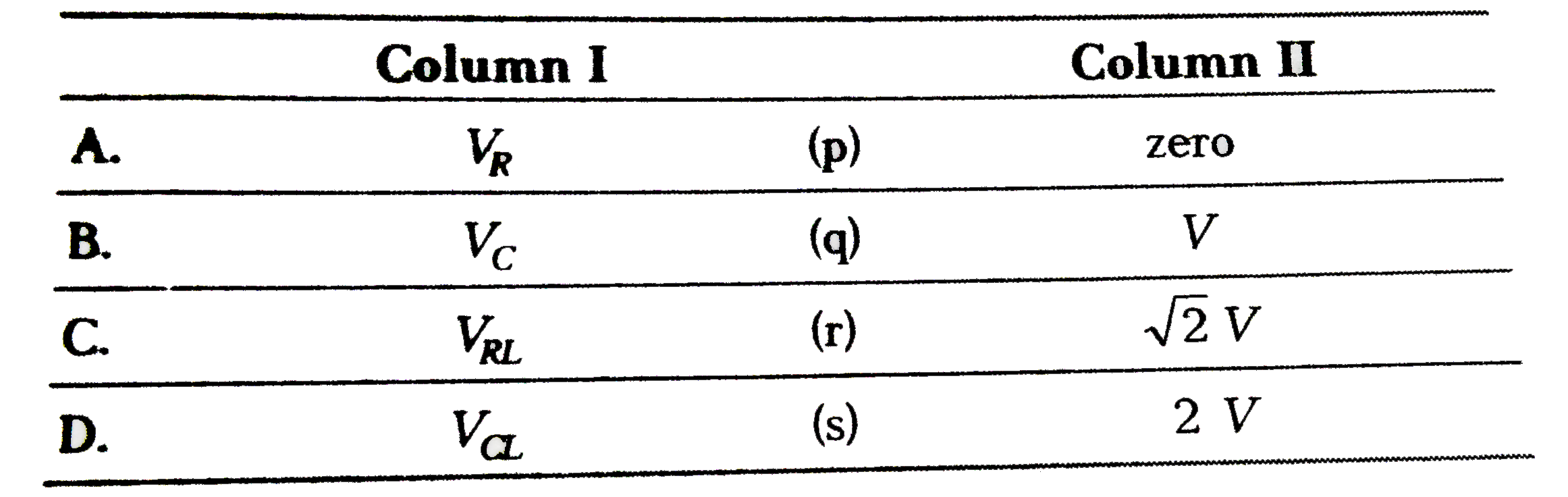
View SolutionIn an L-C-R series circuit R = 10Ω,XL=8Ωand XC=6Ωthe total impedance of the circuit is -
View SolutionIn a given series LCR circuit R=4Ω,XL=5Ω and XC=8Ω, the current
View SolutionIn series LCR circuit voltage leads the current. When
(Given that ω0 = resonant angular frequency)
View SolutionIn an AC series circuit, R=10Ω,XL=20Ω and XC=10Ω.Then, choose the correct options
View SolutionIn an L C R circuit having L = 8 H, C = 0 5μF and R=100Ω in series, the resonance frequency in rad/s is
View SolutionAn L−C−R series circuit has a maximum current of 5A. If L=0.5H and C=8μF, then the angular frequency of AC voltage is
View SolutionIn a series LR circuit (L=3H,R=1.5Ω) and DC voltage =1V. Find current at T=2 seconds.
View Solution
