In series LCR circuit voltage leads the current. When
(Given that ω0 = resonant angular frequency)
ω<ω0
ω=ω0
ω>ω0
None of these
The correct Answer is:C
To solve the problem of when the voltage leads the current in a series LCR circuit, we can follow these steps:
1. Understanding the Circuit: In a series LCR circuit, we have an inductor (L), a capacitor (C), and a resistor (R) connected in series. The behavior of the circuit is influenced by the relationship between the inductive reactance (X_L) and the capacitive reactance (X_C).
2. Voltage Relationships: The voltage across the inductor (V_L) leads the current (I) by 90 degrees, while the voltage across the capacitor (V_C) lags the current by 90 degrees. For the voltage to lead the current, the voltage across the inductor must be greater than the voltage across the capacitor:
VL>VC
3. Expressing Voltages: The voltages across the inductor and capacitor can be expressed in terms of current (I):
VL=I⋅XLandVC=I⋅XC
4. Setting Up the Inequality: From the condition VL>VC, we can substitute the expressions for the voltages:
I⋅XL>I⋅XC
Since the current (I) is common and non-zero, we can divide both sides by I:
XL>XC
5. Substituting Reactances: The inductive reactance XL and capacitive reactance XC are given by:
XL=ωLandXC=1ωC
Thus, we can rewrite the inequality:
ωL>1ωC
6. Rearranging the Inequality: Multiplying both sides by ω (assuming ω>0):
ω2L>1C
7. Final Form: Rearranging gives us:
ω2>1LC
Taking the square root of both sides, we find:
ω>1√LC
8. Resonant Frequency: The resonant angular frequency ω0 is defined as:
ω0=1√LC
Therefore, we conclude that:
ω>ω0
Conclusion:
In a series LCR circuit, the voltage leads the current when the angular frequency ω is greater than the resonant angular frequency ω0.
VL>VC
VL=I⋅XLandVC=I⋅XC
I⋅XL>I⋅XC
Since the current (I) is common and non-zero, we can divide both sides by I:
XL>XC
XL=ωLandXC=1ωC
Thus, we can rewrite the inequality:
ωL>1ωC
ω2L>1C
ω2>1LC
Taking the square root of both sides, we find:
ω>1√LC
ω0=1√LC
Therefore, we conclude that:
ω>ω0
In a series LCR circuit, the voltage leads the current when the angular frequency ω is greater than the resonant angular frequency ω0.
Similar Questions
In series LCR circuit at resonance
View SolutionAssertion : In series L−C−R circuit, voltage will lead the current function for frequency greater than the resonance frequency.
Reason : At resonance frequency, phase difference between current function and voltage function is zero.
View SolutionIn series LCR AC circuit, the voltage of the source at any instant is equal to
View SolutionPhase relationship between current (l) and applied voltage (E) for a series LCR circuit is shown here. ω0 = Resonant angular frequency of the circuit and ω= Applied angular frequency .
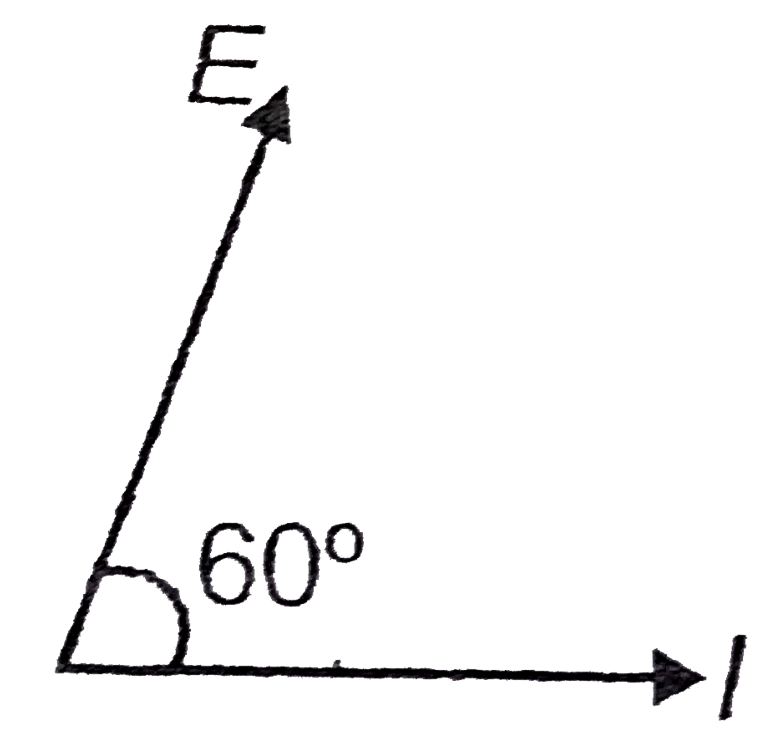
View SolutionIn a series LCR circuit, obtain an expression for the resonant frequency.
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionSTATEMENT - 1 : In a series L-C-R circuit, it is found that voltage leads current. When the capacitance of the circuit is increased, the power consumption will increase.
and
STATEMENT - 2 : The average power consumption at resonance is independent of inductor of capacitor.
View SolutionIn LCR circuit during resonance
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View Solution
