A capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
The correct Answer is:6
To solve the problem step by step, we will use the principles of energy conservation in the LC circuit formed by the capacitor and the inductor.
Step 1: Calculate the initial energy stored in the capacitor
The energy stored in a capacitor is given by the formula:
E=12CV2
where C is the capacitance and V is the voltage.
Given:
- C=2μF=2×10−6F
- V=12V
Substituting the values:
Einitial=12×(2×10−6)×(122)
Einitial=12×(2×10−6)×144
Einitial=(1×10−6)×144=144×10−6J=0.000144J
Step 2: Write the expression for final energy in the circuit
When the capacitor is connected to the inductor, the energy will be distributed between the capacitor and the inductor. The final energy in the circuit can be expressed as:
Efinal=12CV21+12LI2
where V1 is the voltage across the capacitor at the moment of interest and I is the current.
Given:
- V1=6V
- L=0.6mH=0.6×10−3H
Substituting the values:
Efinal=12×(2×10−6)×(62)+12×(0.6×10−3)×I2
Efinal=(1×10−6)×36+(0.3×10−3)I2
Efinal=36×10−6+0.3×10−3I2
Step 3: Apply conservation of energy
According to the conservation of energy:
Einitial=Efinal
Substituting the values:
144×10−6=36×10−6+0.3×10−3I2
Step 4: Solve for I2
Rearranging the equation:
144×10−6−36×10−6=0.3×10−3I2
108×10−6=0.3×10−3I2
Dividing both sides by 0.3×10−3:
I2=108×10−60.3×10−3=1080.3×10−3=360×10−3
Step 5: Calculate I
Taking the square root:
I=√360×10−3=6×10−1=0.6A
Thus, the current in the circuit when the potential difference across the capacitor is 6.0V is 0.6A.
---
The energy stored in a capacitor is given by the formula:
E=12CV2
where C is the capacitance and V is the voltage.
- C=2μF=2×10−6F
- V=12V
Einitial=12×(2×10−6)×(122)
Einitial=12×(2×10−6)×144
Einitial=(1×10−6)×144=144×10−6J=0.000144J
When the capacitor is connected to the inductor, the energy will be distributed between the capacitor and the inductor. The final energy in the circuit can be expressed as:
Efinal=12CV21+12LI2
where V1 is the voltage across the capacitor at the moment of interest and I is the current.
- V1=6V
- L=0.6mH=0.6×10−3H
Efinal=12×(2×10−6)×(62)+12×(0.6×10−3)×I2
Efinal=(1×10−6)×36+(0.3×10−3)I2
Efinal=36×10−6+0.3×10−3I2
According to the conservation of energy:
Einitial=Efinal
Substituting the values:
144×10−6=36×10−6+0.3×10−3I2
Rearranging the equation:
144×10−6−36×10−6=0.3×10−3I2
108×10−6=0.3×10−3I2
I2=108×10−60.3×10−3=1080.3×10−3=360×10−3
Taking the square root:
I=√360×10−3=6×10−1=0.6A
Similar Questions
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. At an instant when potential difference across the capacitor is 6V, what is the current(in A)?
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
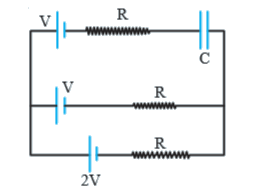
View Solution
Knowledge Check
A condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor when the potential difference across the condenser reduces to V2 is
A(C(V1−V2)2L)12BC(V21−V22)LCC(V21+V22)LD(C(V21−V22)L)12
given that potential differene across 1μF capacitor is 10V. Then,
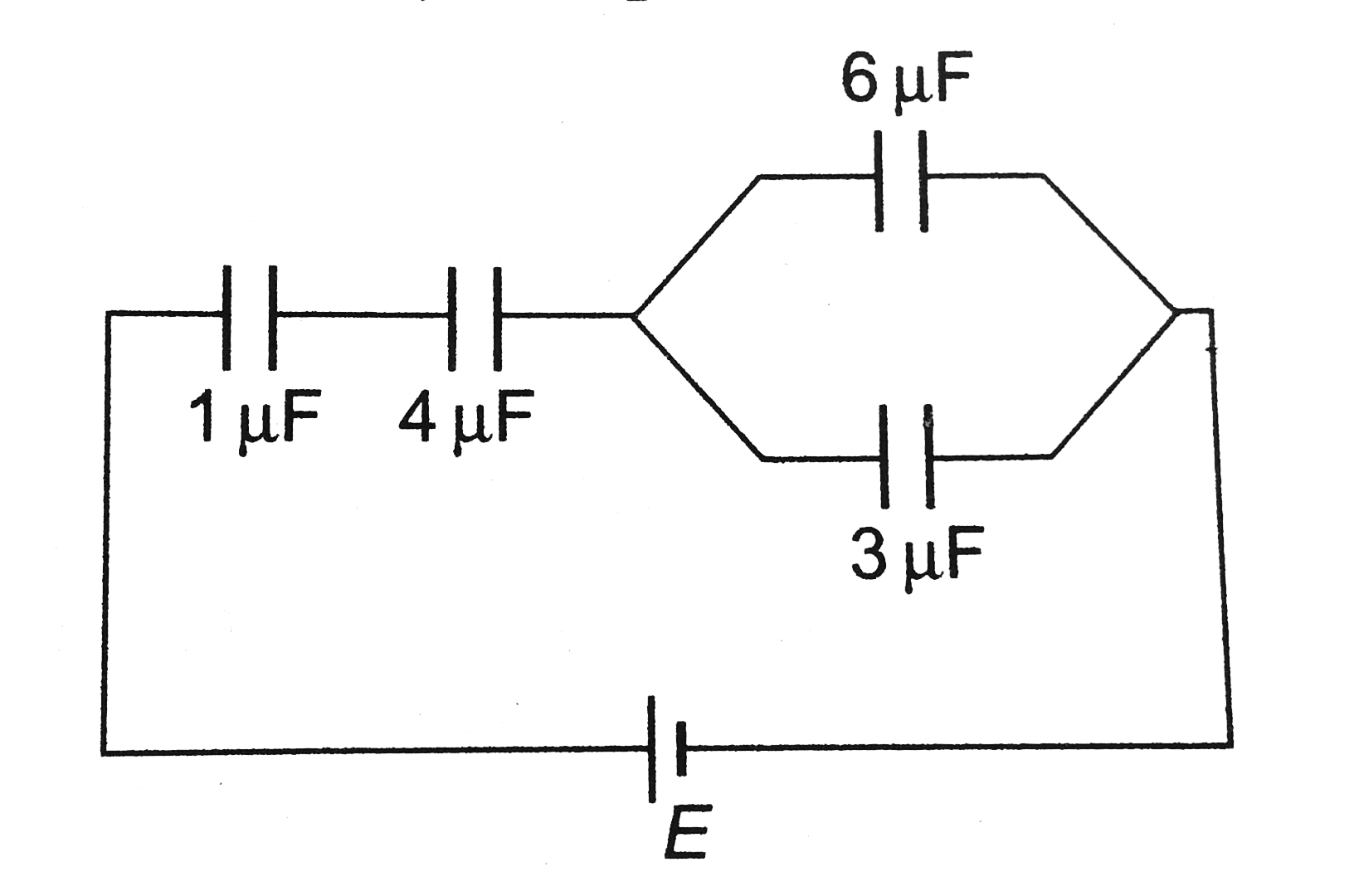
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
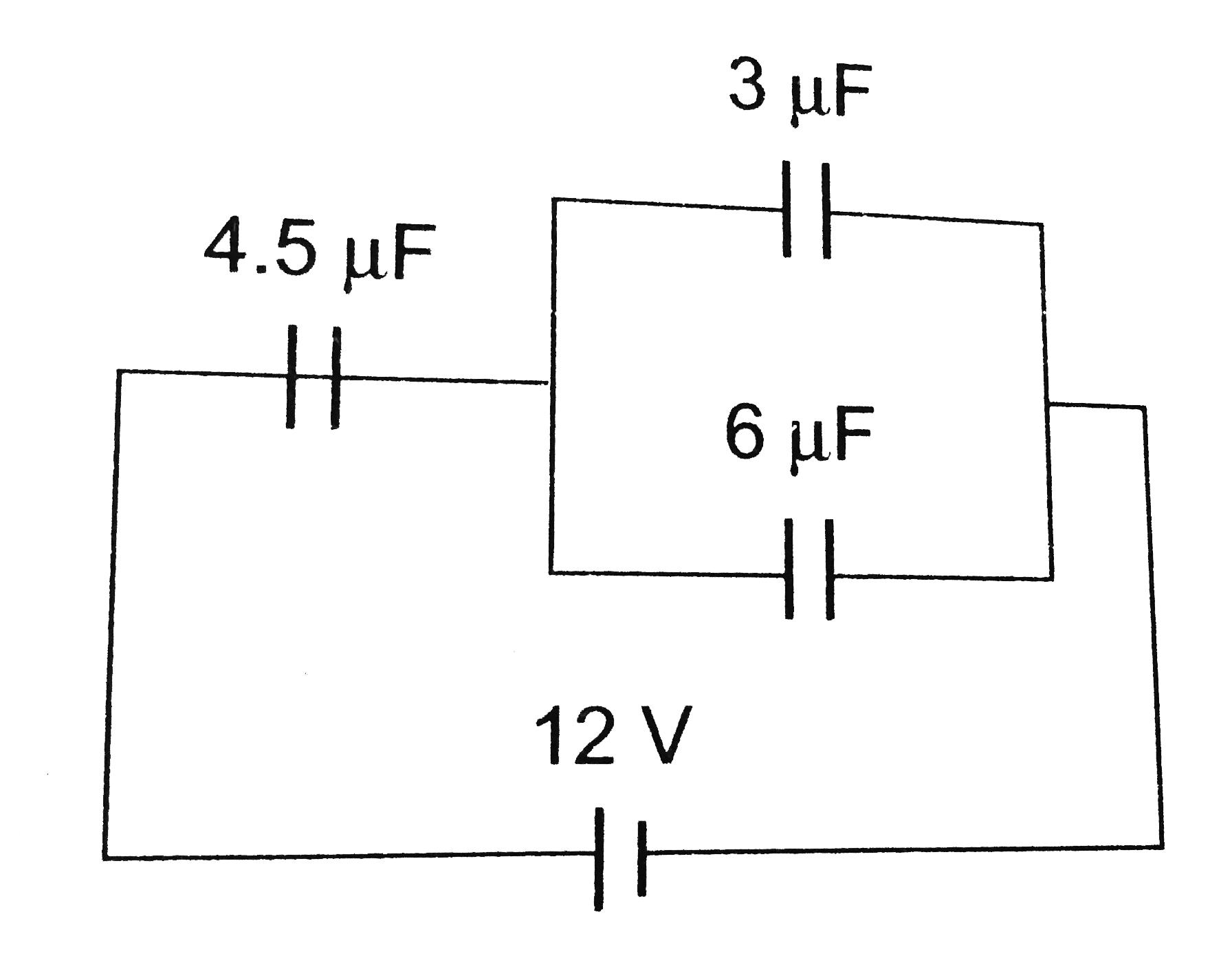
View SolutionIn the adjoning figure, the potential difference across the 4.5μF capacitor is

View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionIn the given circuit, find the potential differece across the 6μf capacitor in steady state.
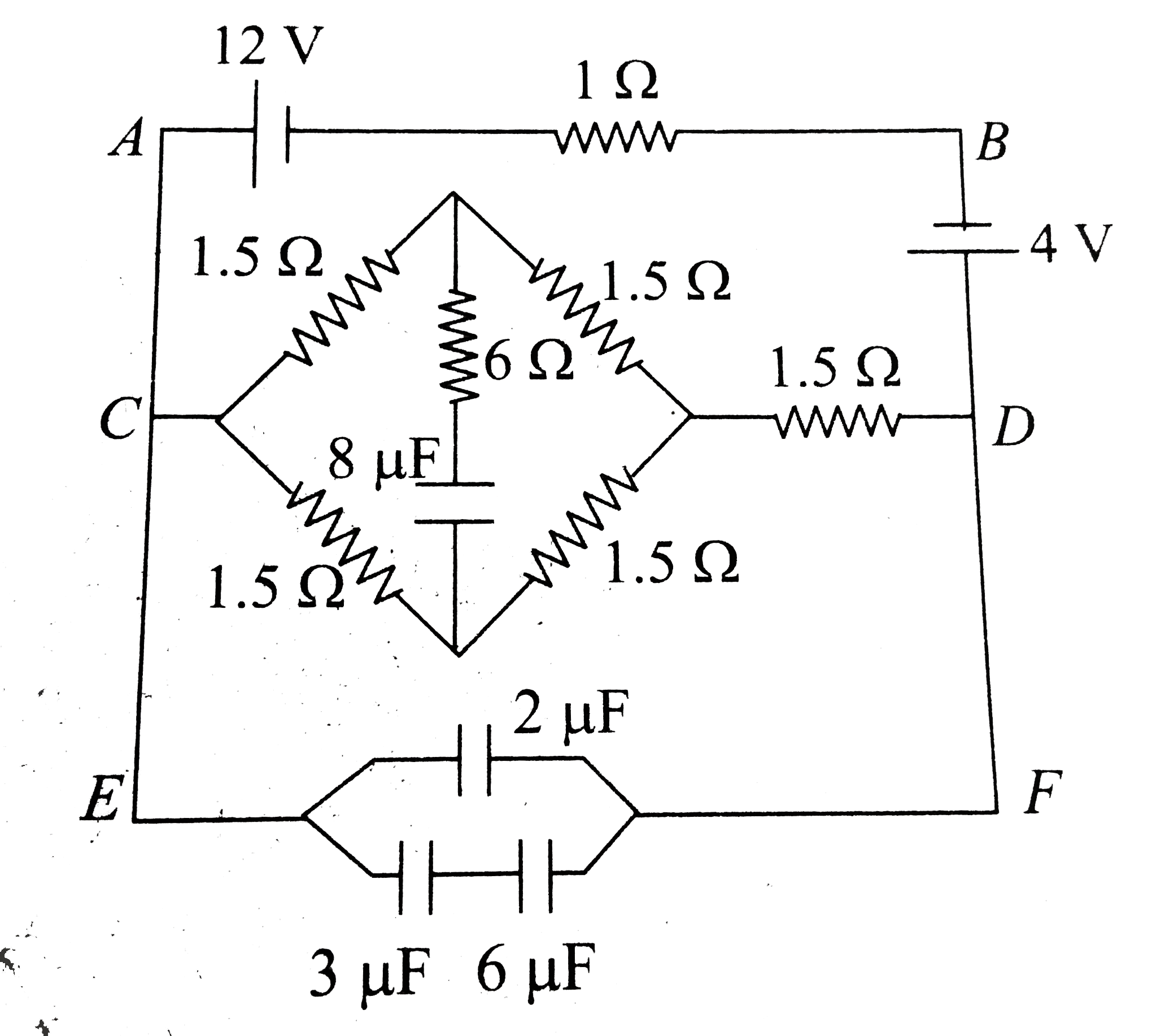
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
View SolutionA condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor wehnn the potential difference across the condenser reduces to V2 is
View Solution
