A capacitor of capacity is charged to a potential difference of 12V. It is then connected across an inductor of inductance . At an instant when potential difference across the capacitor is 6V, what is the current(in A)?
The correct Answer is:A, B, C, D
To solve the problem, we need to find the current flowing through the inductor at the moment when the potential difference across the capacitor is 6V. We will use the principle of conservation of energy in an LC circuit.
1. Identify the given values:
- Capacitance of the capacitor, C=2μF=2×10−6F
- Initial potential difference across the capacitor, V0=12V
- Inductance of the inductor, L=6μH=6×10−6H
- Potential difference across the capacitor at the instant of interest, V=6V
2. Calculate the initial energy stored in the capacitor:
The energy stored in the capacitor when it is charged to V0 is given by the formula:
UC=12CV20
Substituting the values:
UC=12×(2×10−6)×(12)2
UC=12×(2×10−6)×144=1.44×10−4J
3. Calculate the energy stored in the capacitor when the voltage is 6V:
The energy stored in the capacitor at this moment is:
U′C=12CV2
Substituting the values:
U′C=12×(2×10−6)×(6)2
U′C=12×(2×10−6)×36=3.6×10−5J
4. Calculate the energy stored in the inductor:
The total energy in the circuit must remain constant, so we can find the energy stored in the inductor UL at this instant:
UL=UC−U′C=1.44×10−4J−3.6×10−5J
UL=1.08×10−4J
5. Relate the energy in the inductor to the current:
The energy stored in the inductor is given by:
UL=12LI2
Setting this equal to the energy we calculated:
1.08×10−4=12×(6×10−6)×I2
6. Solve for the current I:
Rearranging the equation:
I2=2×1.08×10−46×10−6
I2=2.16×10−46×10−6=36
I=√36=6A
Final Answer:
The current flowing through the inductor at the instant when the potential difference across the capacitor is 6V is 6 A.
- Capacitance of the capacitor, C=2μF=2×10−6F
- Initial potential difference across the capacitor, V0=12V
- Inductance of the inductor, L=6μH=6×10−6H
- Potential difference across the capacitor at the instant of interest, V=6V
The energy stored in the capacitor when it is charged to V0 is given by the formula:
UC=12CV20
Substituting the values:
UC=12×(2×10−6)×(12)2
UC=12×(2×10−6)×144=1.44×10−4J
The energy stored in the capacitor at this moment is:
U′C=12CV2
Substituting the values:
U′C=12×(2×10−6)×(6)2
U′C=12×(2×10−6)×36=3.6×10−5J
The total energy in the circuit must remain constant, so we can find the energy stored in the inductor UL at this instant:
UL=UC−U′C=1.44×10−4J−3.6×10−5J
UL=1.08×10−4J
The energy stored in the inductor is given by:
UL=12LI2
Setting this equal to the energy we calculated:
1.08×10−4=12×(6×10−6)×I2
Rearranging the equation:
I2=2×1.08×10−46×10−6
I2=2.16×10−46×10−6=36
I=√36=6A
The current flowing through the inductor at the instant when the potential difference across the capacitor is 6V is 6 A.
Similar Questions
A capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacitance 1μF is charged to potential 2 V and is connected to an inductor of 1 mH. At an instant when potential difference across. The capacitor is 1 V, the current in the circuit is 10−2√10x3 ampere. Find out the value of x.
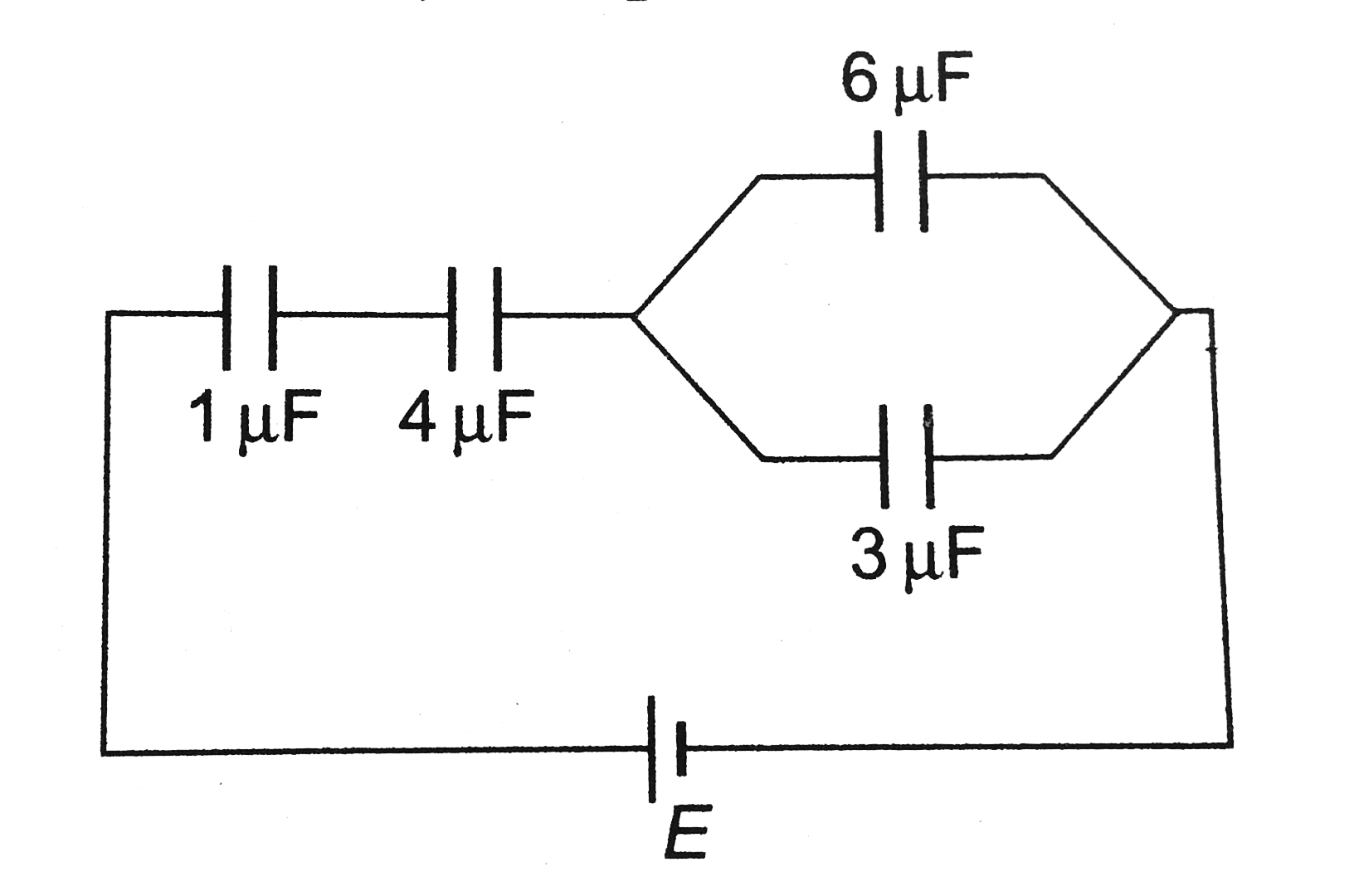
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
View SolutionA 100μF capacitor is charged to a potential difference of 24V. It is connected to an uncharged capacitor of capacitance 20μF What will be the new potential difference across the 100μF capacitor?
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionThe potential drop across 7μF capacitor is 6V. Then
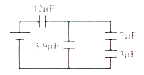
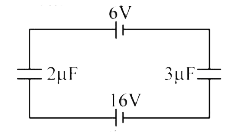
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
View Solution
