In a certain circuit current changes with time accroding to i=2√t. r.m.s. value of current between t=2 to t=4s will be
The correct Answer is:6
To find the root mean square (r.m.s.) value of the current i=2√t between t=2 seconds and t=4 seconds, we can follow these steps:
Step 1: Understand the formula for r.m.s. value
The r.m.s. value of a current over a time interval can be calculated using the formula:
Irms=√1T∫t2t1i2dt
where T=t2−t1.
Step 2: Set up the integral for i2
Given i=2√t, we first need to calculate i2:
i2=(2√t)2=4t
Step 3: Set the limits of integration
We are given the limits t1=2 seconds and t2=4 seconds.
Step 4: Calculate the integral of i2
Now we need to evaluate the integral:
∫424tdt
This can be simplified as:
=4∫42tdt
Step 5: Evaluate the integral
The integral ∫tdt is:
∫tdt=t22
Thus, we have:
4(t22)42=4(422−222)
Calculating this gives:
=4(162−42)=4(8−2)=4×6=24
Step 6: Calculate the total time interval T
The total time interval T is:
T=t2−t1=4−2=2
Step 7: Calculate the r.m.s. value
Now we can calculate the r.m.s. value:
Irms=√1T∫t2t1i2dt=√12⋅24=√12=2√3
Final Answer
Thus, the r.m.s. value of the current between t=2 seconds and t=4 seconds is:
Irms=2√3 A
The r.m.s. value of a current over a time interval can be calculated using the formula:
Irms=√1T∫t2t1i2dt
where T=t2−t1.
Given i=2√t, we first need to calculate i2:
i2=(2√t)2=4t
We are given the limits t1=2 seconds and t2=4 seconds.
Now we need to evaluate the integral:
∫424tdt
This can be simplified as:
=4∫42tdt
The integral ∫tdt is:
∫tdt=t22
Thus, we have:
4(t22)42=4(422−222)
Calculating this gives:
=4(162−42)=4(8−2)=4×6=24
The total time interval T is:
T=t2−t1=4−2=2
Now we can calculate the r.m.s. value:
Irms=√1T∫t2t1i2dt=√12⋅24=√12=2√3
Thus, the r.m.s. value of the current between t=2 seconds and t=4 seconds is:
Irms=2√3 A
Similar Questions
Knowledge Check
In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1s
If i=t2,0<t<T then r.m.s. value of current is
View Solutionr.m.s. value of current i=3+4sin(ωt+π/3) is:
View SolutionThe instantaneous current in an AC circuit is l = √2sin(50 t + π / 4 ) . The rms value of current is
View SolutionThe charge on a capacitor plate in a circuit, as a function of time, is shown in the figure. What is the value of current at t=4s?
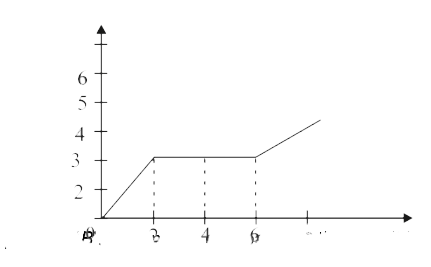
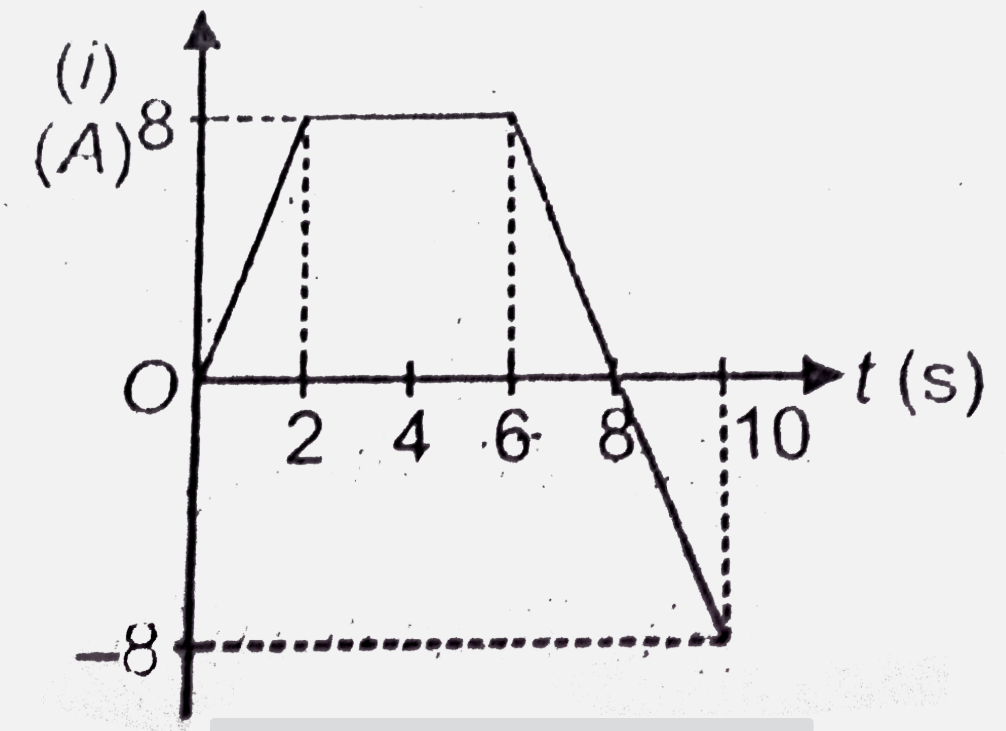
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionFlux ϕ (in weber) in a closed circuit of resistance5 omega varies with time (in second) according to equation ϕ=3t2−5t+2. The magnitude of average induced current between0 to 2s is
View Solution
