If I is moment of inertia, F is force, v is velocity, E is energy and L is length then, dimension of (IFv2EL4) will be:
[MLT−2]
[MT−2]
[ML2T−3]
[LT−1]
The correct Answer is:B
We knows,
Dimensions of moment of inertia = [ML2]
Dimensions of moment of force F=[MLT−2]
Dimensions of moment of velocity (v)=[LT−2]
Dimensions of moment of work (W)=[ML2T−2]
Dimensions of moment of length (l)=[L]
Here, Dimensions of [X]=Dimensions of [IFv2]Dimensions of [WL3]
=[ML2][MLT−2][LT−2]2[ML2T−2][L3]
[M2L5T−4][ML−5T−2]=[MT−2]
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS Book:DC PANDEY ENGLISHChapter:UNITS, DIMENSIONS & ERROR ANALYSIS Exercise:Match the column
Explore 6 Videos
- UNIT AND DIMENSIONSBook:DC PANDEY ENGLISHChapter:UNIT AND DIMENSIONSExercise:Assertion And Reason
Explore 2 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
Similar Questions
Consider the equation F=a2be−bxE where F is force x is distance E is energy and a, b are constants. What are the dimensions of a and b?
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
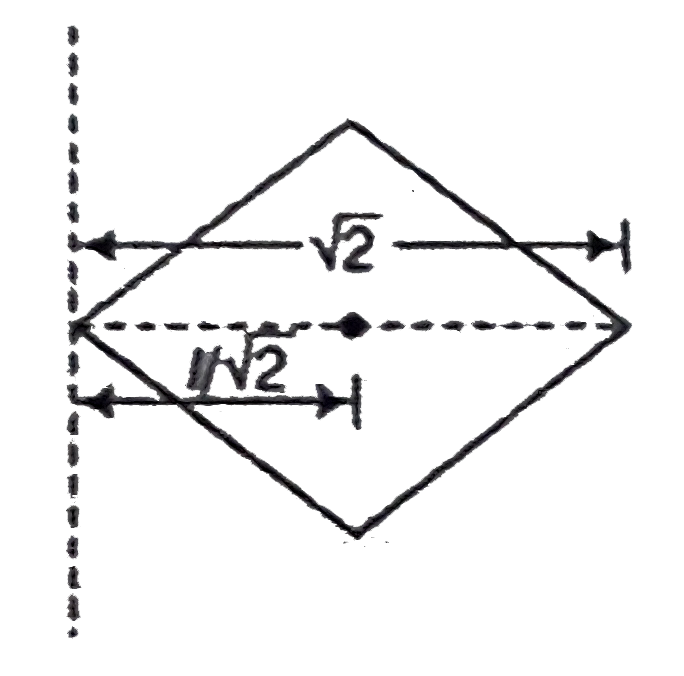
View SolutionThe moment of inertia of a door of mass m, length 2l and width l about its longer side is.
View SolutionIf F is the force, v is the velocity and A is the area, considered as fundamental quantity . Find the dimension of youngs modulus.
View SolutionIf force (F), velocity (V) and time (T) are taken as fundamental units, then the dimensions of mass are
View SolutionIf force (F), velocity (V) and time (T) are taken as fundamental units, then the dimensions of mass are
View SolutionIf the energy ( E) ,velocity (v) and force (F) be taken as fundamental quantities,then the dimension of mass will be
View SolutionIf the energy ( E) ,velocity (v) and force (F) be taken as fundamental quantities,then the dimension of mass will be
View SolutionIf E = energy , G= gravitational constant, I=impulse and M=mass, then dimensions of GIM2E2 are same as that of
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View Solution