The moment of inertia of a door of mass m, length 2l and width l about its longer side is.
11ml224
5ml224
ml23
none of these
The correct Answer is:C
To find the moment of inertia of a door of mass m, length 2l, and width l about its longer side, we can follow these steps:
1. Understand the Geometry:
- The door has a mass m, length 2l, and width l.
- We will calculate the moment of inertia about the longer side, which is along the length 2l.
2. Set Up the Coordinate System:
- Place the door in the coordinate system such that the longer side (length 2l) is along the x-axis.
- The center of the door will be at the origin, so the edges will be at −l and l along the x-axis, and the width l extends along the y-axis from −l2 to l2.
3. Consider an Elemental Strip:
- Take a vertical strip of width dx at a distance x from the origin. The height of this strip is l.
- The elemental mass dm of this strip can be expressed as:
dm=mArea⋅Area of strip=m2l⋅l⋅(l⋅dx)=m2l⋅dx
4. Calculate the Moment of Inertia of the Strip:
- The moment of inertia dI of this elemental strip about the axis (longer side) is given by:
dI=dm⋅x2=(m2l⋅dx)⋅x2
5. Integrate to Find Total Moment of Inertia:
- The total moment of inertia I is obtained by integrating dI from −l to l:
I=∫l−ldI=∫l−l(m2l⋅x2⋅dx)
- Factor out the constant:
I=m2l∫l−lx2dx
6. Evaluate the Integral:
- The integral ∫l−lx2dx can be calculated as:
∫x2dx=x33∣∣l−l=l33−(−l33)=2l33
- Substitute this back into the equation for I:
I=m2l⋅2l33=ml23
7. Final Result:
- The moment of inertia of the door about its longer side is:
I=ml23
- The door has a mass m, length 2l, and width l.
- We will calculate the moment of inertia about the longer side, which is along the length 2l.
- Place the door in the coordinate system such that the longer side (length 2l) is along the x-axis.
- The center of the door will be at the origin, so the edges will be at −l and l along the x-axis, and the width l extends along the y-axis from −l2 to l2.
- Take a vertical strip of width dx at a distance x from the origin. The height of this strip is l.
- The elemental mass dm of this strip can be expressed as:
dm=mArea⋅Area of strip=m2l⋅l⋅(l⋅dx)=m2l⋅dx
- The moment of inertia dI of this elemental strip about the axis (longer side) is given by:
dI=dm⋅x2=(m2l⋅dx)⋅x2
- The total moment of inertia I is obtained by integrating dI from −l to l:
I=∫l−ldI=∫l−l(m2l⋅x2⋅dx)
- Factor out the constant:
I=m2l∫l−lx2dx
- The integral ∫l−lx2dx can be calculated as:
∫x2dx=x33∣∣l−l=l33−(−l33)=2l33
- Substitute this back into the equation for I:
I=m2l⋅2l33=ml23
- The moment of inertia of the door about its longer side is:
I=ml23
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
View SolutionIn Fig. find moment of inertia of a plate having mass M, length l and width b about axes 1,2,3 and 4. Assume that C is the centre and mass is uniformly distributed.
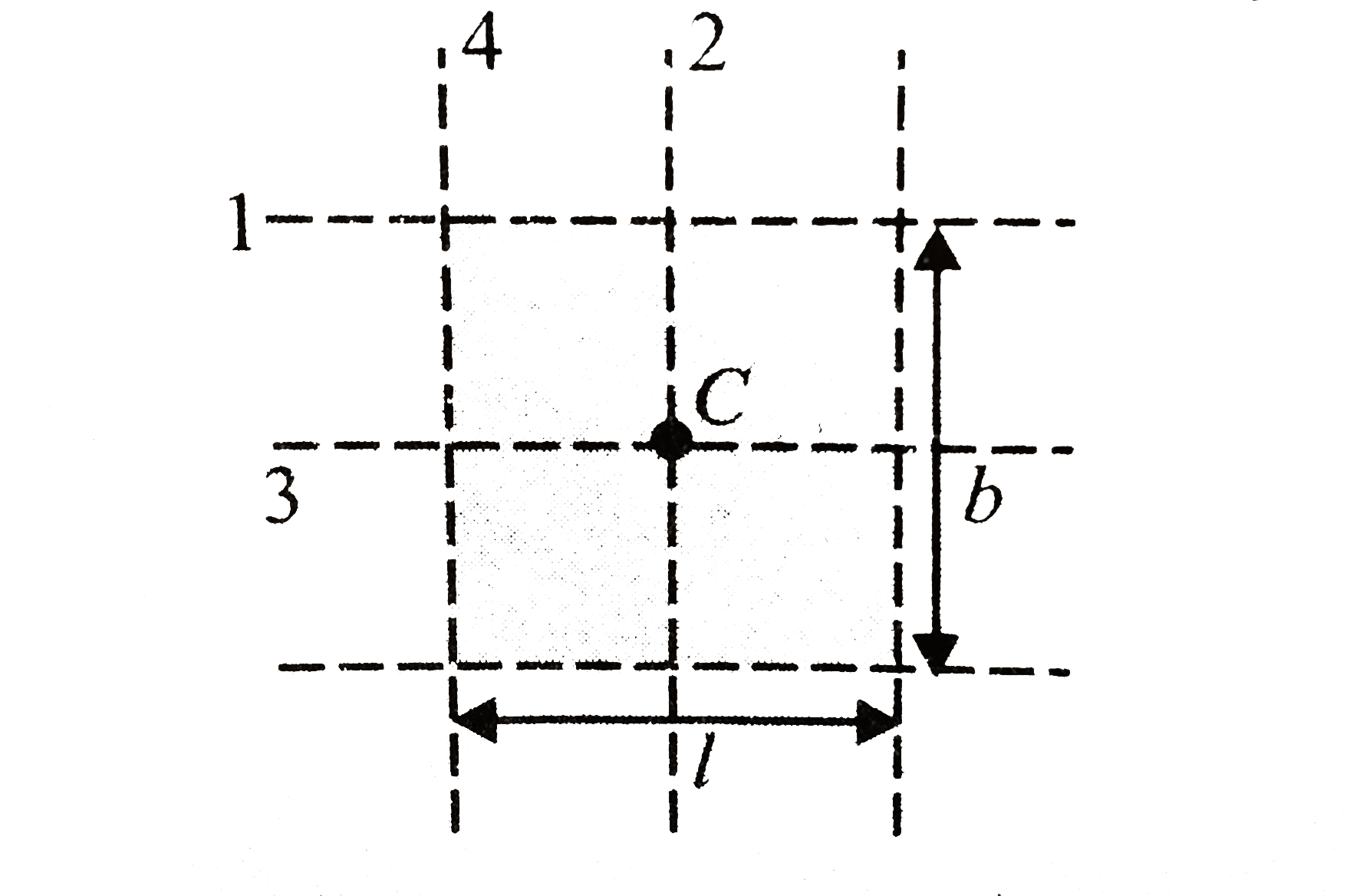
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
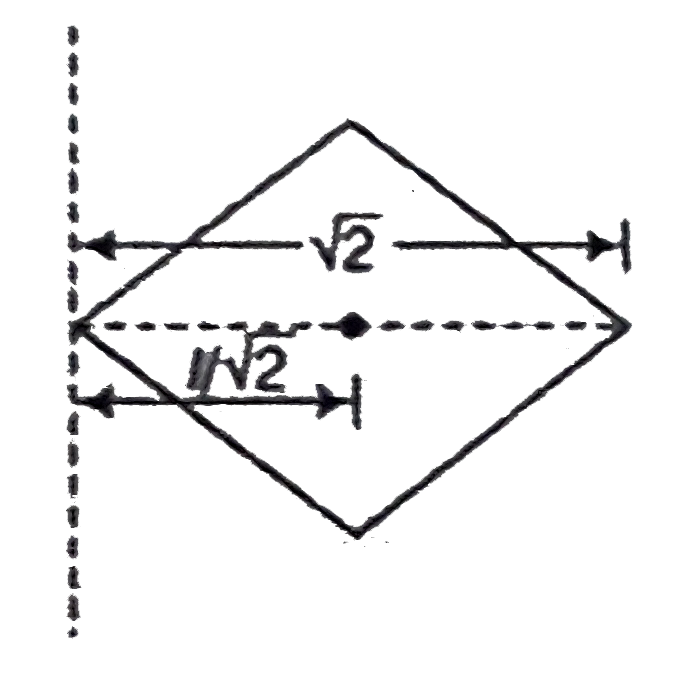
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionMoment of inertia of a rod of mass m and length l about its one end is I. If one-fourth of its length is cut away, then moment of inertia of the remaining rod about its one end will be
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View Solution
