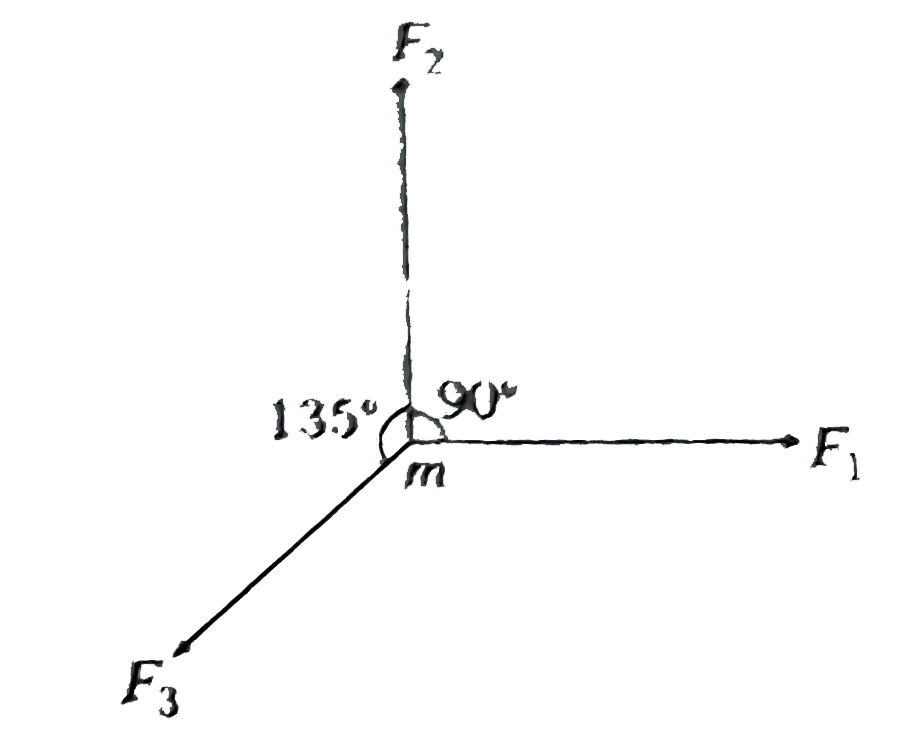
When a force F acts on a body of mass m the acceleration product in the body is a . If three equal forces F1=F2=F3=F act on the same body as shown in figure the acceleration produced is
(√2−1)a
(√2+1)a
√2a
a
The correct Answer is:A
(a) Accelertion a=Fm
Resultant of F1andF2will be
F12=√2F(in opposite directiomn o fF3)
Now ,resultant ofF12andF3will be ,
Fnet=(√2−1)F
∴a=Fnetm=(√2−1)Fm=(√2−1)a
Topper's Solved these Questions
Similar Questions
When a force F acs on a body of mass m the acceleration product in the body is a . If htree equal forces F1=F2=F3=F act on the same body as shown in figure the accleration produced is
 View Solution
View SolutionA force of 10 N acts on a body of mass 5 kg. Find the acceleration produced.
View SolutionA force of 15 N acts on a body of mass 2 kg. Calculate the acceleration produced.
View SolutionA force of 15 N acts on a body of mass 2 kg. Calculate the acceleration produced.
View SolutionTwo forces F1 and F2 are acting on a rod abc as shown in figure.
 View Solution
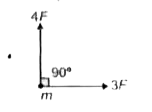
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
 View Solution
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
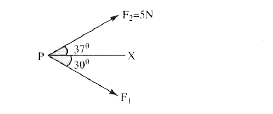 View Solution
View SolutionA force produces an acceleration of a1 in a body and the same force produces an acceleration of a2 in another body. If the two bodies are combined and the same force is applied on the combination, the acceleration produced in it is
View SolutionA force produces an acceleration of 4ms−2 in a body of mass m1 and the same force produces an acceleration of 6ms−2 in another body oa mass m2. If the same force is applied to (m1+m2), then the acceleration will be
View SolutionA force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.
 View Solution
View Solution

