In the arrangement shown, all the surface are smooth, strings and pulleys are light. Find the tension in the string.
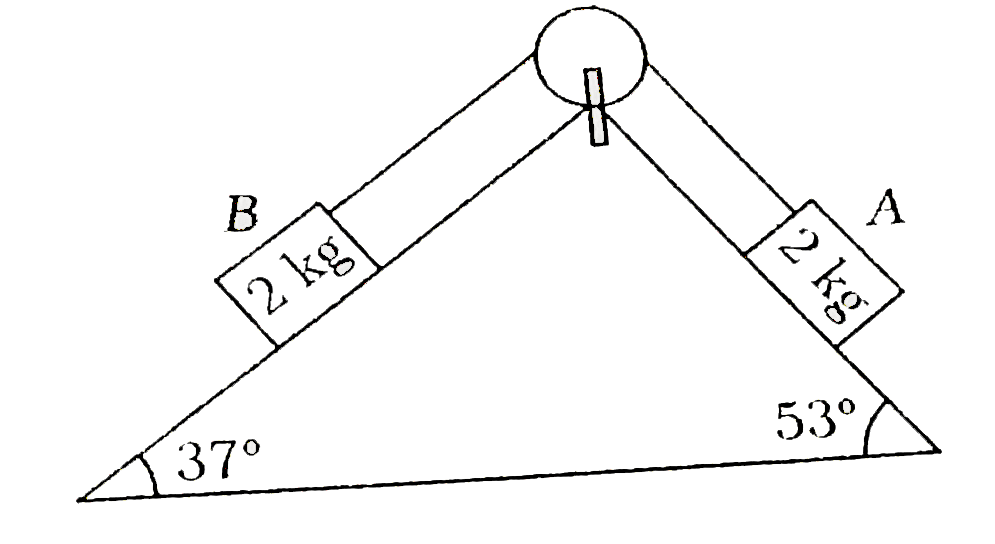
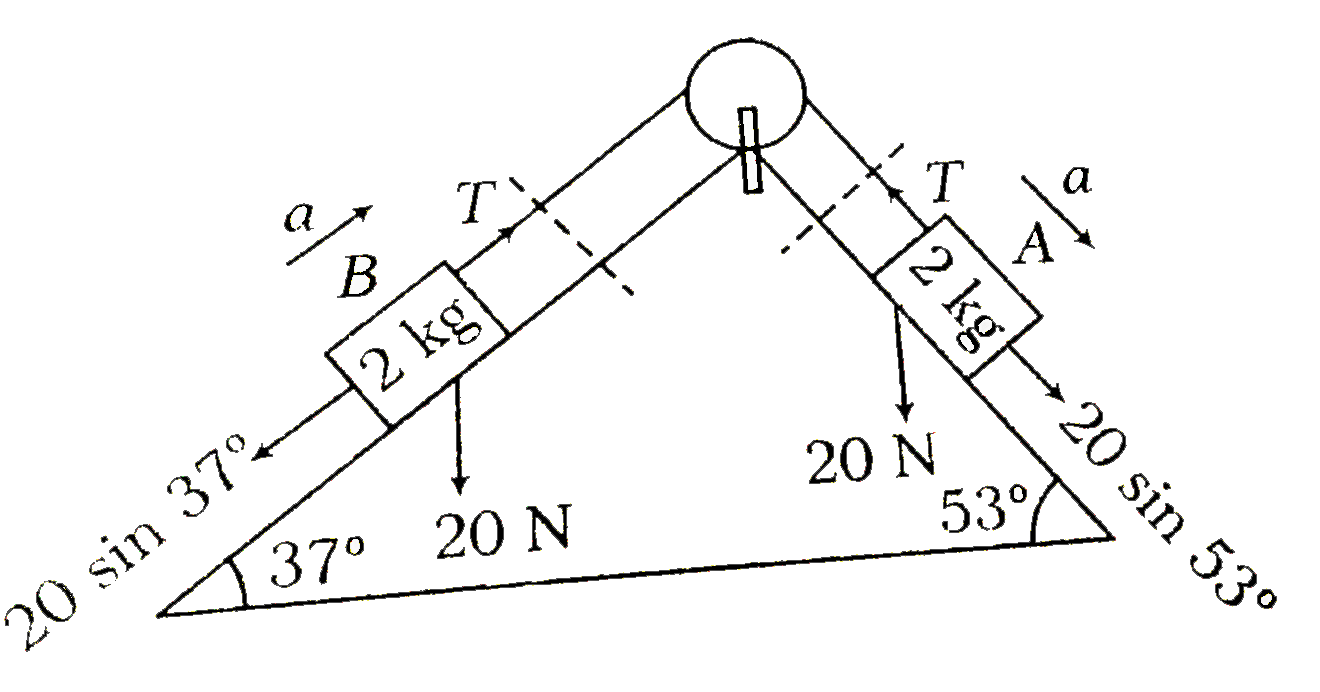
Block A : along the plane
20sin53∘−T=2a …(i)
Block B: along the plane
T−20sin37∘=2a ……(ii)
Adding Eqs. (i) and (ii), we get
20(sin53∘−sin37∘)=4a
20(45−35)=4=4a⇒a=1ms−2
T=20sin37∘+2a=20×35+2×1=14N
Similar Questions
In the arrangement shown, inclined plane is smooth, strings and pulleys are massless. Find T1T2
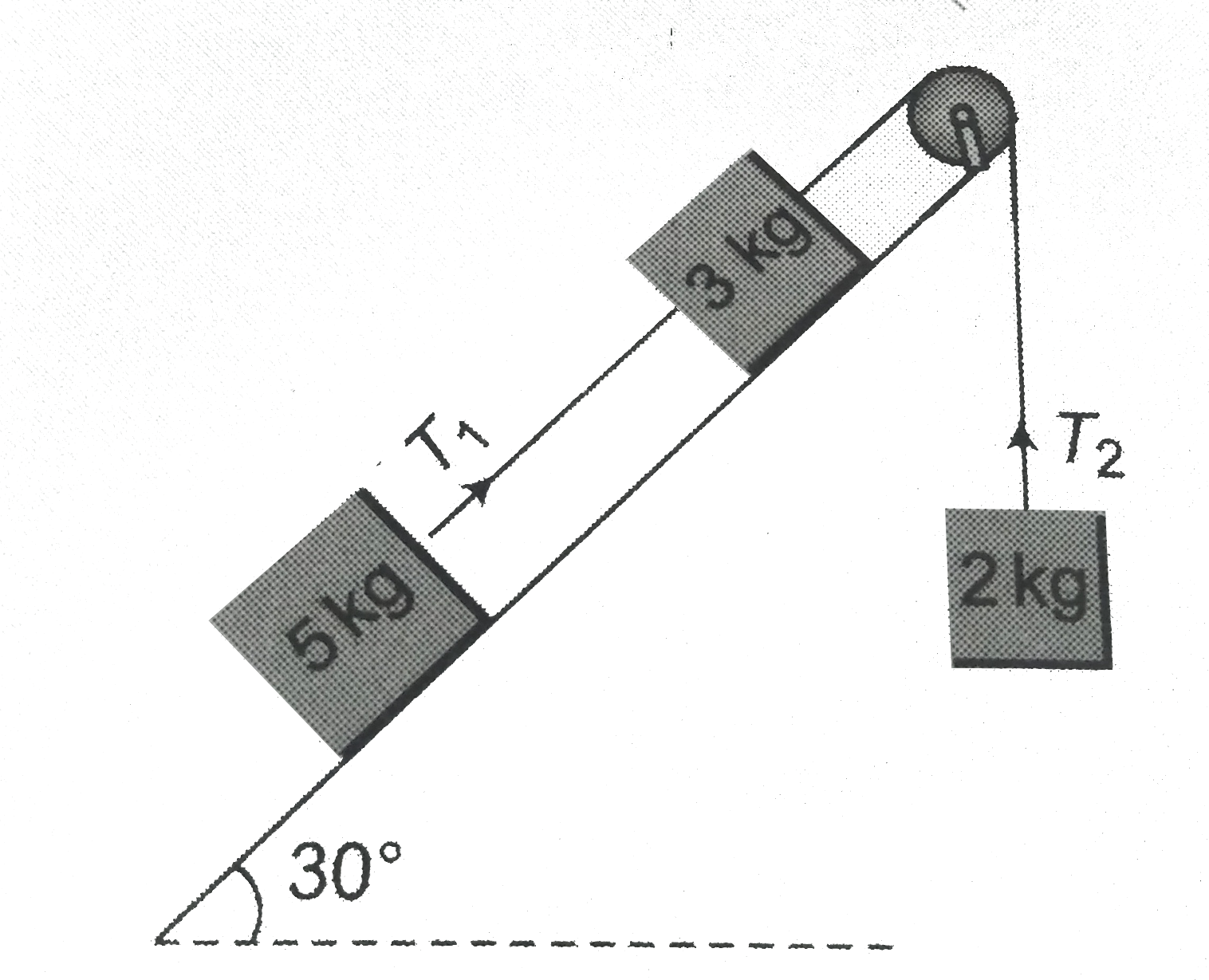 View Solution
View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.
 View Solution
View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).
 View Solution
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
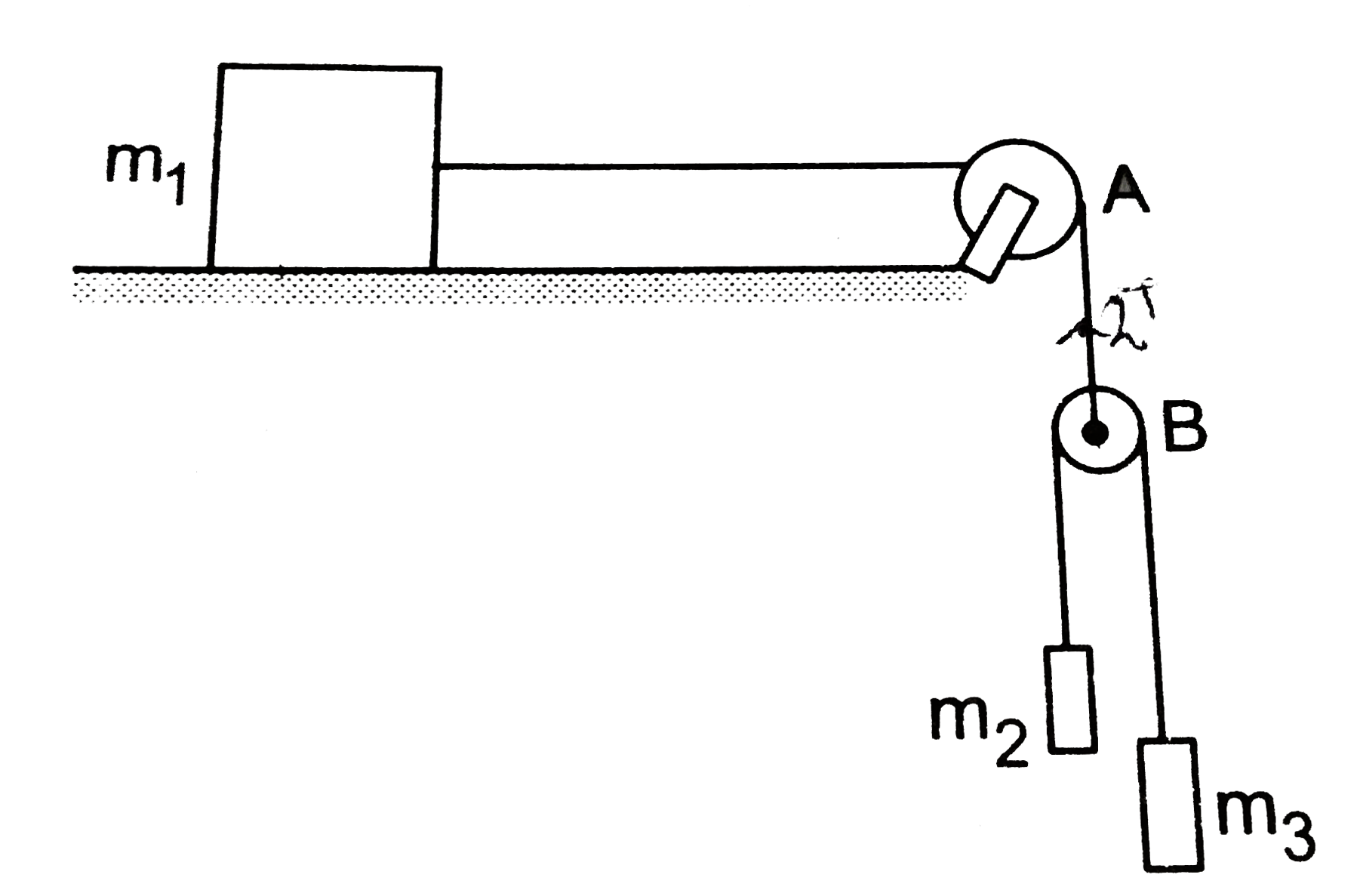 View Solution
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
 View Solution
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.
 View Solution
View SolutionIn the arrangement shown, the 2 kg block is held to keep the system at rest. The string and pulley are ideal. When the 2kg block is set free, by what amount the tension in the string changes? [g=10m/s2]
 View Solution
View SolutionFor the system shown in the figure, the pulleys are light and frictionless. The tension in the string will be (Assume all surfaces to be smooth)
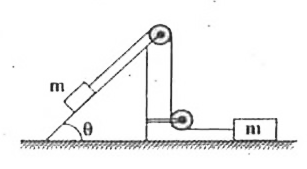 View Solution
View SolutionThe intial configuration of the system is as shown in the figure.
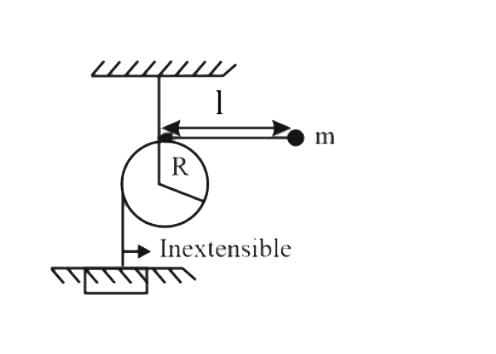
The string and the pulley are light. The bob is released and the string starts wrapping around the pulley. (The pulley is held in place by a force applied at the centre)

Find the rate r at which the length of the string warpped around the pulley increaes (as a function of θ).View SolutionIn the system shown in figure all surfaces are smooth. Strings is massless and inextensible.Find acceleration of the system and tension T in the string (g=10m/s2)
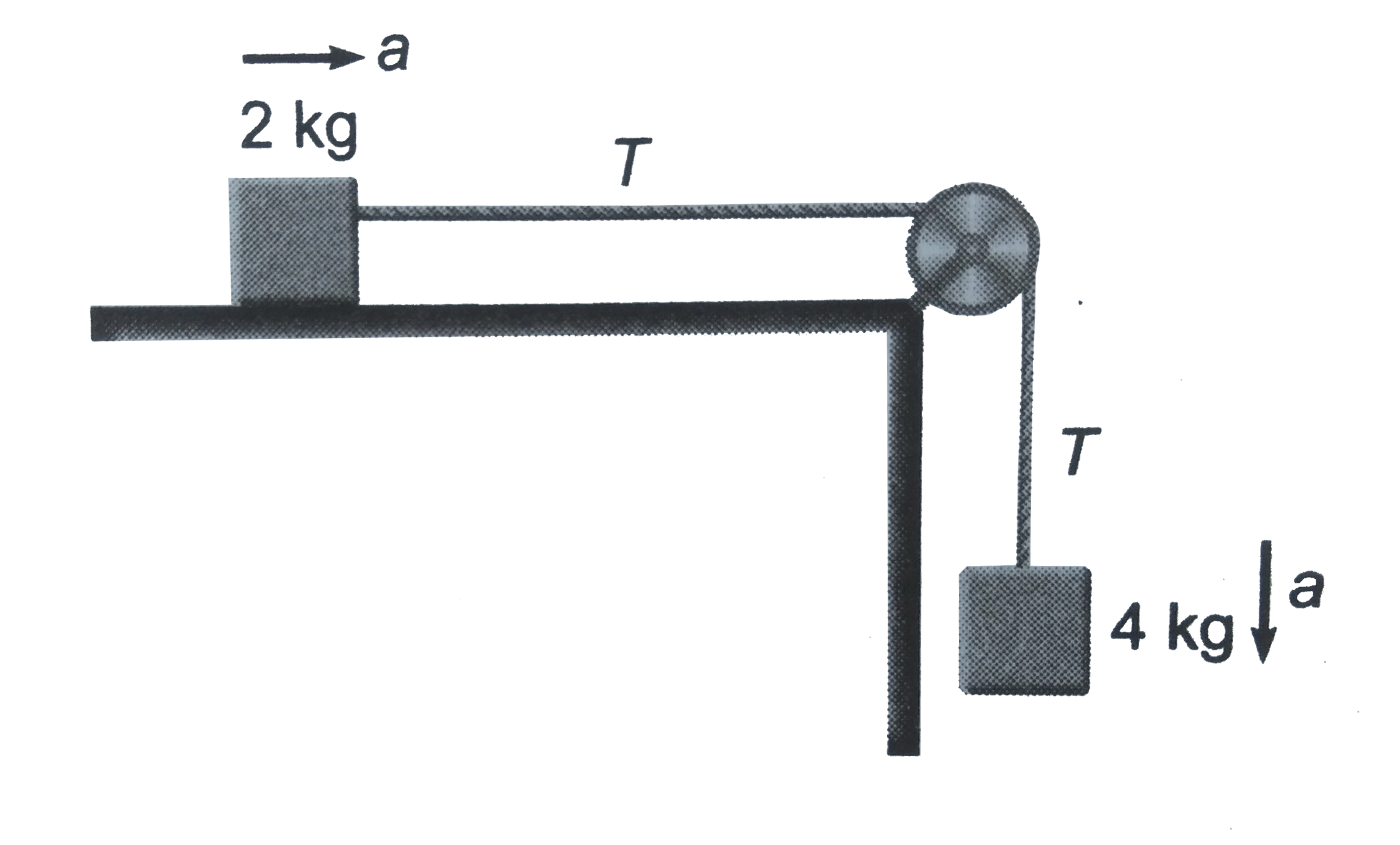 View Solution
View Solution

