For a particle in S.H.M. if the maximum acceleration is a and maximum velocity is v then amplitude is
va
v2a
v22a
va
The correct Answer is:B
To find the amplitude of a particle in simple harmonic motion (SHM) given the maximum acceleration a and maximum velocity v, we can follow these steps:
1. Understand the formulas for maximum velocity and acceleration in SHM:
- The maximum velocity Vmax of a particle in SHM is given by:
Vmax=ωA
- The maximum acceleration Amax is given by:
Amax=ω2A
2. Set the maximum acceleration and maximum velocity equal to the given values:
- We know from the problem that:
Amax=aandVmax=v
3. Express ω in terms of A:
- From the equation for maximum velocity:
v=ωA⇒ω=vA(Equation 1)
4. Substitute ω into the equation for maximum acceleration:
- Substitute ω from Equation 1 into the equation for maximum acceleration:
a=ω2A
- This becomes:
a=(vA)2A
5. Simplify the equation:
- Rearranging gives:
a=v2A
6. Solve for amplitude A:
- Rearranging the equation to solve for A:
A=v2a
Final Answer:
The amplitude A is given by:
A=v2a
- The maximum velocity Vmax of a particle in SHM is given by:
Vmax=ωA
- The maximum acceleration Amax is given by:
Amax=ω2A
- We know from the problem that:
Amax=aandVmax=v
- From the equation for maximum velocity:
v=ωA⇒ω=vA(Equation 1)
- Substitute ω from Equation 1 into the equation for maximum acceleration:
a=ω2A
- This becomes:
a=(vA)2A
- Rearranging gives:
a=v2A
- Rearranging the equation to solve for A:
A=v2a
The amplitude A is given by:
A=v2a
Similar Questions
A particle is executing a simple harmonic motion. Its maximum acceleration is α and maximum velocity is β. Then, its time period of vibration will be
View SolutionPassage XI) The differential equation of a particle undergoing SHM is given by ad2xdt2+bx = 0. The particle starts from the extreme position.
The ratio of the maximum acceleration to the maximum velocity of the particle isView Solution
Knowledge Check
- Question 1 - Select One
A particle executing simple harmonic motion with an amplitude A and angularr frequency ω. The ratio of maximum acceleration to the maximum velocity of the particle is
AωABω2ACωDω2A
If a particle is executing S.H.M. then the graph between its acceleration and velocity is , in general
View SolutionThe maximum acceleration of a simple harmonic oscillator is a0 and maximum velocity is v0. What is the amplitude?
View SolutionMaximum acceleration of a particle in SHM is 16cm/s2 and maximum uelocity is 8cm/s.Find time period and amplitude of oscillations.
View SolutionWhat is the ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator?
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
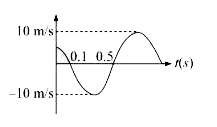 View Solution
View SolutionTwo identical pendulums oscillate with a constant phase difference π4 and same amplitude. If the maximum velocity of one is v, the maximum velocity of the other will be.
View SolutionA particle is executing S.H.M. with amplitude A and has maximum velocity v0. Its speed at displacement 3A4 will be
View Solution

