If a particle is executing S.H.M. then the graph between its acceleration and velocity is , in general
An ellipse
A circle
A parabola
A hyperbola
The correct Answer is:1
To solve the problem of finding the relationship between acceleration and velocity for a particle executing Simple Harmonic Motion (SHM), we can follow these steps:
1. Understand the Basic Equations of SHM:
- The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
2. Find the Velocity:
- The velocity v is the derivative of displacement with respect to time:
v(t)=dxdt=Aωcos(ωt)
3. Find the Acceleration:
- The acceleration a is the derivative of velocity with respect to time:
a(t)=dvdt=−Aω2sin(ωt)
4. Relate Velocity and Acceleration:
- From the equations for velocity and acceleration, we have:
- v=Aωcos(ωt)
- a=−Aω2sin(ωt)
5. Express sin(ωt) and cos(ωt):
- From the velocity equation, we can express cos(ωt):
cos(ωt)=vAω
- From the acceleration equation, we can express sin(ωt):
sin(ωt)=−aAω2
6. Use the Pythagorean Identity:
- We know that sin2(ωt)+cos2(ωt)=1. Substituting the expressions from above:
(−aAω2)2+(vAω)2=1
- This simplifies to:
a2A2ω4+v2A2ω2=1
7. Rearranging the Equation:
- Multiply through by A2ω4:
a2+v2ω2=A2ω4
- This is the equation of an ellipse in the a-v plane.
8. Conclusion:
- The graph between acceleration a and velocity v for a particle in SHM is an ellipse.
Final Answer:
The graph between acceleration and velocity for a particle executing SHM is an ellipse.
---
- The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
- The velocity v is the derivative of displacement with respect to time:
v(t)=dxdt=Aωcos(ωt)
- The acceleration a is the derivative of velocity with respect to time:
a(t)=dvdt=−Aω2sin(ωt)
- From the equations for velocity and acceleration, we have:
- v=Aωcos(ωt)
- a=−Aω2sin(ωt)
- From the velocity equation, we can express cos(ωt):
cos(ωt)=vAω
- From the acceleration equation, we can express sin(ωt):
sin(ωt)=−aAω2
- We know that sin2(ωt)+cos2(ωt)=1. Substituting the expressions from above:
(−aAω2)2+(vAω)2=1
- This simplifies to:
a2A2ω4+v2A2ω2=1
- Multiply through by A2ω4:
a2+v2ω2=A2ω4
- This is the equation of an ellipse in the a-v plane.
- The graph between acceleration a and velocity v for a particle in SHM is an ellipse.
The graph between acceleration and velocity for a particle executing SHM is an ellipse.
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-C )
Explore 11 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT (SECTION -D( Comprehension) )
Explore 3 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION -A)
Explore 58 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
Similar Questions
Knowledge Check
A particle executing SHM. The phase difference between acceleration and displacement is
A0Bπ2CπD2πA particle executing SHM. The phase difference between velocity and displacement is
A0Bπ2CπD2π
A particle executes linear. If a and v donate the acceleration and velocity of the particle respectively, then correct graph relating the values a2 and v2 is
View SolutionAcceleration displacement (a-x) graph of a particle executing S.H.M. is shown in the figure. The frequency of oscillation is (tanθ=8)
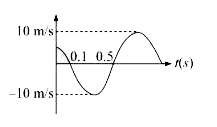
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
View SolutionA particle is executing S.H.M. from mean position at 5 cm distance, acceleration is 20cm/sec2 then value of angular velocity will be
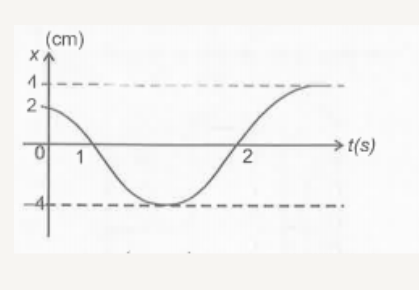
View SolutionDisplacement time(x-t) graph of a particle executing S.H.M is shown In the figure.The equation of S.H.M is given by
View SolutionA particle is executing S.H.M. with amplitude A and has maximum velocity v0. Its speed at displacement 3A4 will be
View Solution