The total energy of a particle having a displacement x, executing simple harmonic motion is
∝x
∝x2
independent of x
∝x1/2
The correct Answer is:C
To solve the question regarding the total energy of a particle executing simple harmonic motion (SHM) with displacement x, we can follow these steps:
Step 1: Understand the Components of Total Energy
The total energy E of a particle in simple harmonic motion is the sum of its kinetic energy (KE) and potential energy (PE).
Step 2: Write the Expressions for Kinetic and Potential Energy
The kinetic energy KE of a particle in SHM is given by:
KE=12mω2(A2−x2)
where:
- m is the mass of the particle,
- ω is the angular frequency,
- A is the amplitude of the motion,
- x is the displacement from the mean position.
The potential energy PE is given by:
PE=12mω2x2
Step 3: Calculate the Total Energy
Now, we can find the total energy E by adding the kinetic and potential energy:
E=KE+PE
Substituting the expressions we have:
E=(12mω2(A2−x2))+(12mω2x2)
Step 4: Simplify the Expression
Now, simplifying the total energy expression:
E=12mω2(A2−x2)+12mω2x2
E=12mω2A2−12mω2x2+12mω2x2
The −12mω2x2 and +12mω2x2 cancel each other out:
E=12mω2A2
Step 5: Conclusion
From the final expression for total energy E=12mω2A2, we can see that the total energy is dependent only on the mass m, angular frequency ω, and amplitude A. It does not depend on the displacement x.
Thus, the total energy of a particle executing simple harmonic motion is independent of x.
Final Answer
The correct option is 3) independent of x.
---
The total energy E of a particle in simple harmonic motion is the sum of its kinetic energy (KE) and potential energy (PE).
The kinetic energy KE of a particle in SHM is given by:
KE=12mω2(A2−x2)
where:
- m is the mass of the particle,
- ω is the angular frequency,
- A is the amplitude of the motion,
- x is the displacement from the mean position.
PE=12mω2x2
Now, we can find the total energy E by adding the kinetic and potential energy:
E=KE+PE
Substituting the expressions we have:
E=(12mω2(A2−x2))+(12mω2x2)
Now, simplifying the total energy expression:
E=12mω2(A2−x2)+12mω2x2
E=12mω2A2−12mω2x2+12mω2x2
The −12mω2x2 and +12mω2x2 cancel each other out:
E=12mω2A2
From the final expression for total energy E=12mω2A2, we can see that the total energy is dependent only on the mass m, angular frequency ω, and amplitude A. It does not depend on the displacement x.
The correct option is 3) independent of x.
Similar Questions
Knowledge Check
Consider the following statements. The total energy of a particles executing simple harmonic motion depends on its
1. amplitude
2. Period
3. displacement of these :A1 and 2 are correctB2 and 3 are correctC1 and 3 are correctD1, 2 and 3 are correctThe kinetic energy and potential energy of a particle executing simple harmonic motion will be equal when displacement (amplitude = a) is
Aa/2Ba√2Ca/√2Da√2/3Which of the following relationships between the acceleration a and the displacement x of a particle executing simple harmonic motion?
Aa=2x2Ba=−2x2Ca=2xDa=−2x
The phase difference between the instantaneous Velocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe displacement of a particle of mass 3g executing simple harmonic motion is given by x=3sin(0.2t) in SI units. The kinetic energy of the particle at a point which is at a displacement equal to 13 of its amplitude from its mean position is
View SolutionQ. Statement I: The total energy of a particle performing simple harmonic motion could be negative. Statement II: Potential energy of a system could be magnetic.
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
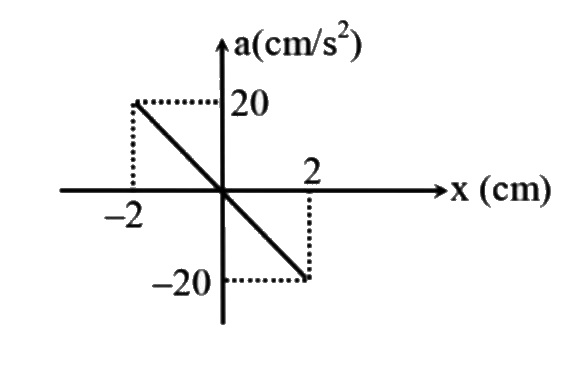
View Solution
