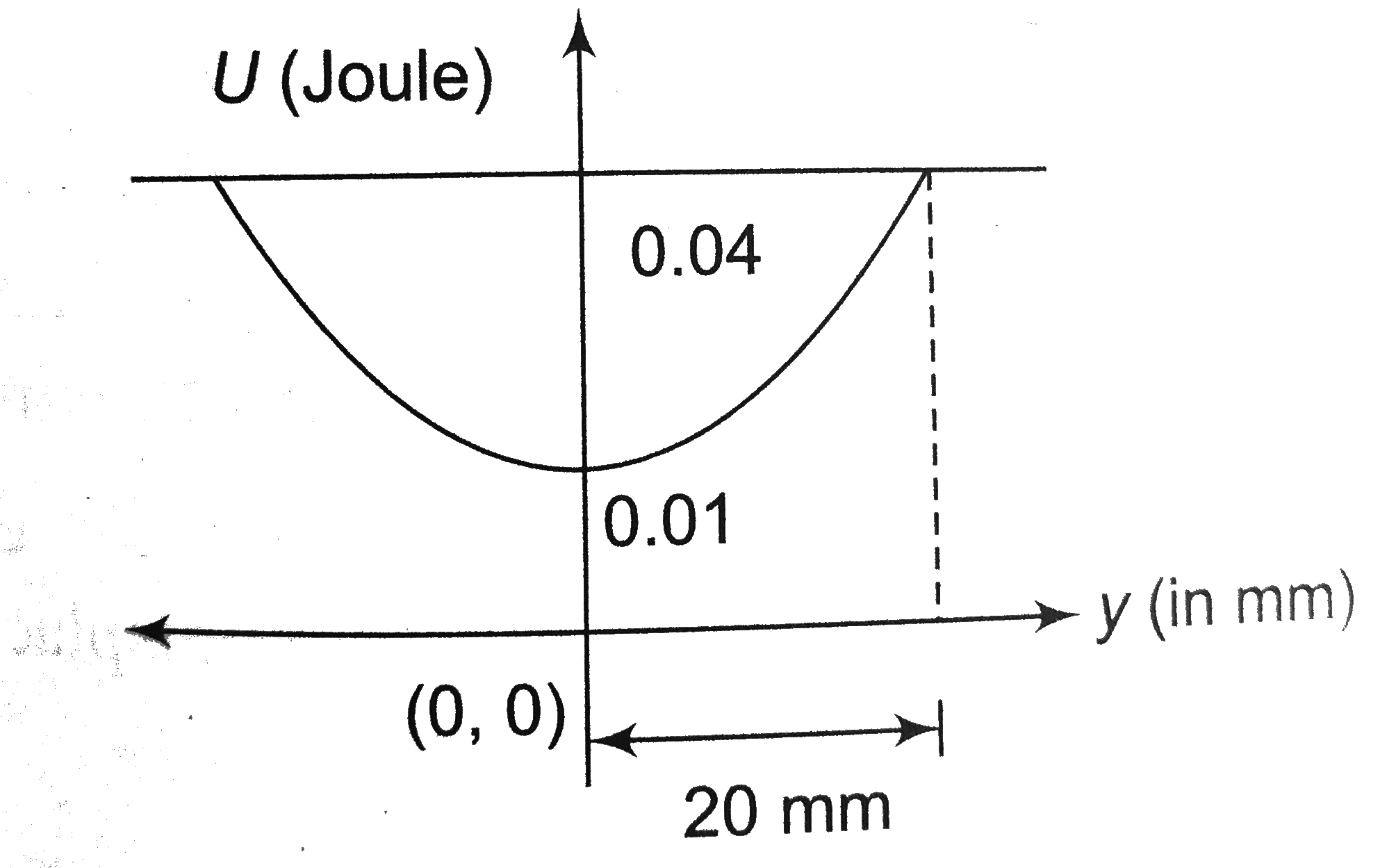
The variation of potential energy of harmonic oscillator is as shown in figure. The spring constant is
1×102Nm−1
1.5×102Nm−1
2×102Nm−1
3×102Nm−1
The correct Answer is:B
(b) 12kA2=(0.04−0.01)J=0.03J
∴k=0.06A2=0.06(0.02)2=150Nm−1
Similar Questions
Knowledge Check
The total energy of a simple harmonic oscillation is proportional to
AamplitudeBsquare of amplitudeCfrequencyDvelocity
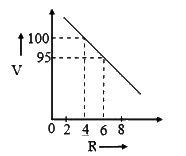
The pointer reading versus load graph for a spring balance is as shown in the figure.
The spring constant is
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

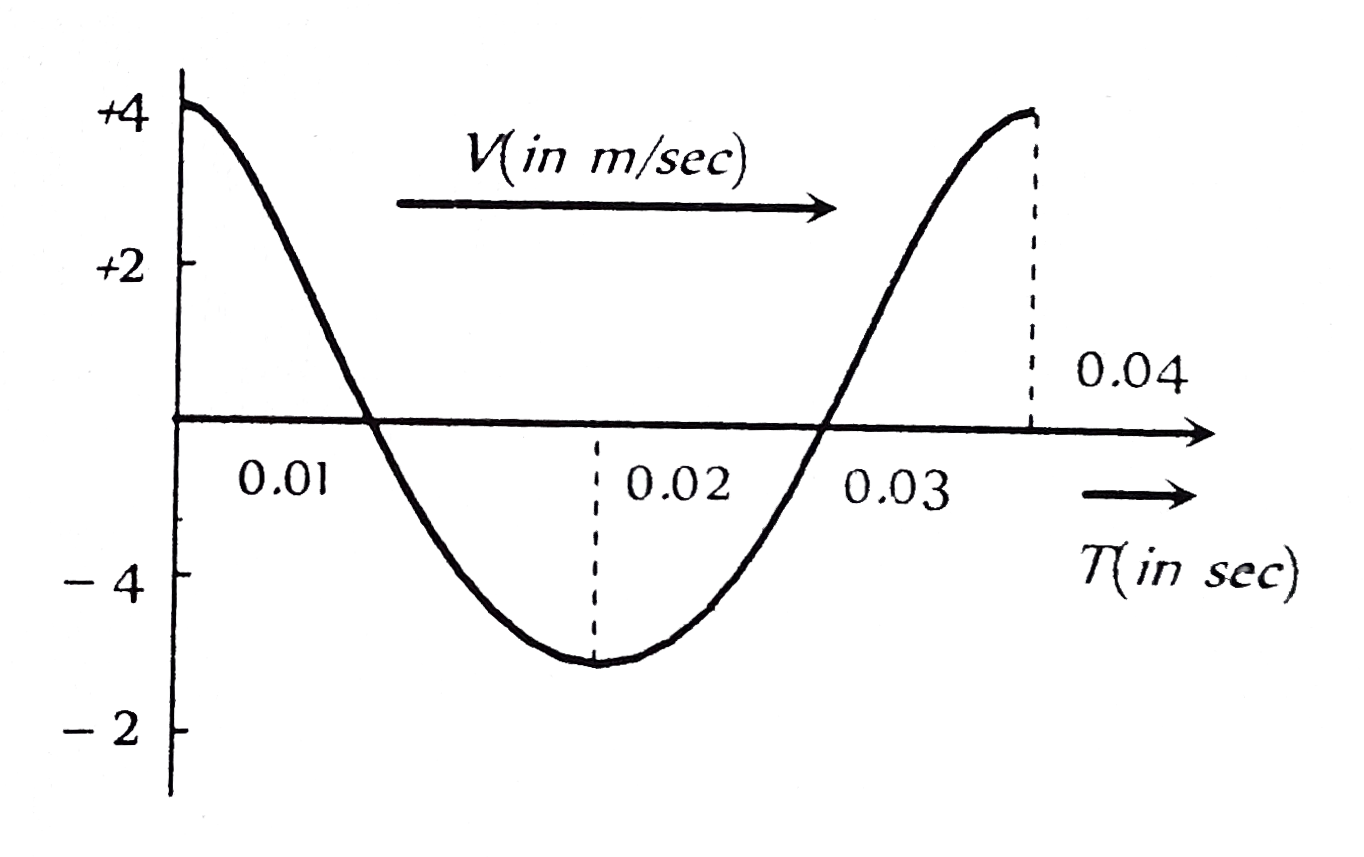
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
View SolutionDraw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
View SolutionThe potential energy of a harmonic oscillation when is half way to its and end point is (where E it’s the total energy)
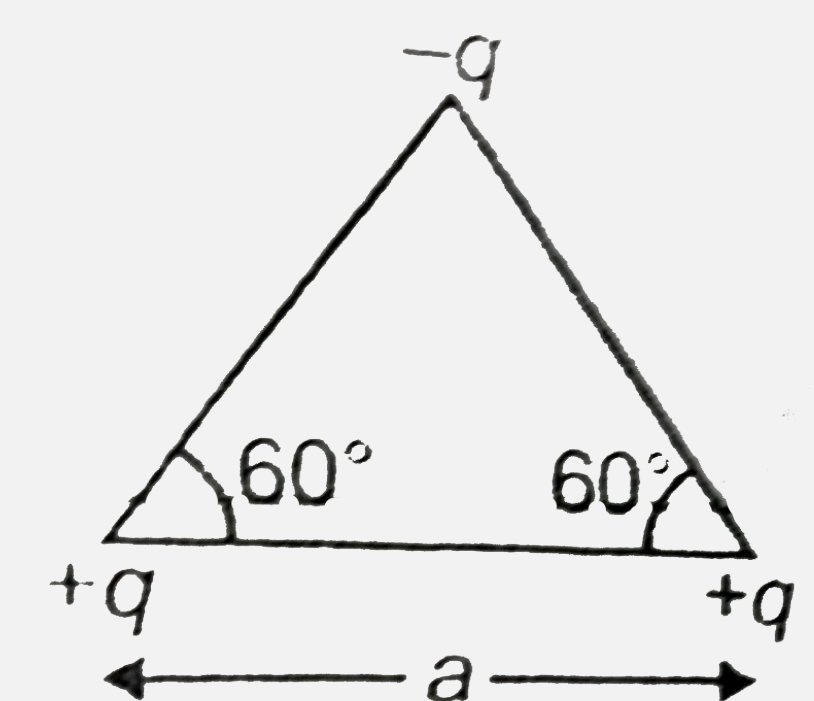
View SolutionFind the electrostatic potential energy of the system shown in the figure
View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
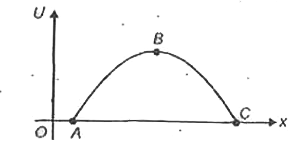
The body is in equilibrium state at
View Solution