Draw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
To solve the problem of drawing the graphs for the potential energy (PE), kinetic energy (KE), and total energy (TE) of a simple harmonic oscillator (SHO) with respect to displacement, we will follow these steps:
Step 1: Understand the Formulas
1. Potential Energy (PE): The potential energy of a simple harmonic oscillator is given by the formula:
PE=12mω2x2
where m is the mass, ω is the angular frequency, and x is the displacement from the mean position.
2. Kinetic Energy (KE): The kinetic energy of the oscillator is given by:
KE=12mω2(A2−x2)
where A is the amplitude of the oscillation.
3. Total Energy (TE): The total energy of the oscillator is the sum of potential and kinetic energy:
TE=PE+KE=12mω2A2
This shows that the total energy is constant and does not depend on displacement x.
Step 2: Determine the Graphs
1. Total Energy (TE): Since total energy is constant, the graph of TE versus displacement will be a horizontal line at the value 12mω2A2.
2. Potential Energy (PE): The potential energy is proportional to x2. Therefore, the graph of PE versus displacement will be a parabola opening upwards, starting from the origin (0,0) and increasing as x moves away from zero.
3. Kinetic Energy (KE): The kinetic energy decreases as potential energy increases. Since KE is given by 12mω2(A2−x2), it will be a downward-opening parabola. The maximum kinetic energy occurs at the mean position (where x=0) and decreases to zero at the extreme positions (where x=±A).
Step 3: Draw the Graphs
1. Set Up Axes: Draw a graph with the x-axis representing displacement x and the y-axis representing energy (PE, KE, TE).
2. Plot Total Energy: Draw a horizontal line at y=12mω2A2 across the graph.
3. Plot Potential Energy: Draw a parabola starting at the origin (0,0) and curving upwards, indicating that PE increases with the square of the displacement.
4. Plot Kinetic Energy: Draw a downward-opening parabola that starts at the maximum value of KE at x=0 and intersects the x-axis at x=±A.
Final Graph
Your final graph will show:
- A horizontal line for Total Energy (TE).
- An upward-opening parabola for Potential Energy (PE).
- A downward-opening parabola for Kinetic Energy (KE).
1. Potential Energy (PE): The potential energy of a simple harmonic oscillator is given by the formula:
PE=12mω2x2
where m is the mass, ω is the angular frequency, and x is the displacement from the mean position.
KE=12mω2(A2−x2)
where A is the amplitude of the oscillation.
TE=PE+KE=12mω2A2
This shows that the total energy is constant and does not depend on displacement x.
1. Total Energy (TE): Since total energy is constant, the graph of TE versus displacement will be a horizontal line at the value 12mω2A2.
1. Set Up Axes: Draw a graph with the x-axis representing displacement x and the y-axis representing energy (PE, KE, TE).
Your final graph will show:
- A horizontal line for Total Energy (TE).
- An upward-opening parabola for Potential Energy (PE).
- A downward-opening parabola for Kinetic Energy (KE).
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
Knowledge Check
The total energy of a simple harmonic oscillation is proportional to
AamplitudeBsquare of amplitudeCfrequencyDvelocityFrequency of variation of kinetic energy of a simple harmonic motion of frequency n is
A2nBnCn2D3n
Draw graphs to show the variation of amplitude with driving frequency of a forced harmonic oscillator under (i) zero damping, (ii) low damping and (iii) high damping
View SolutionDraw a graph showing the variation of decay rate with number of active nuclei.
View SolutionThe graph showing the variation of K.E. or P.E. with displacement of a harmonic oscillator is a parabola, but that of total energy with displacement is a straight line. Why?
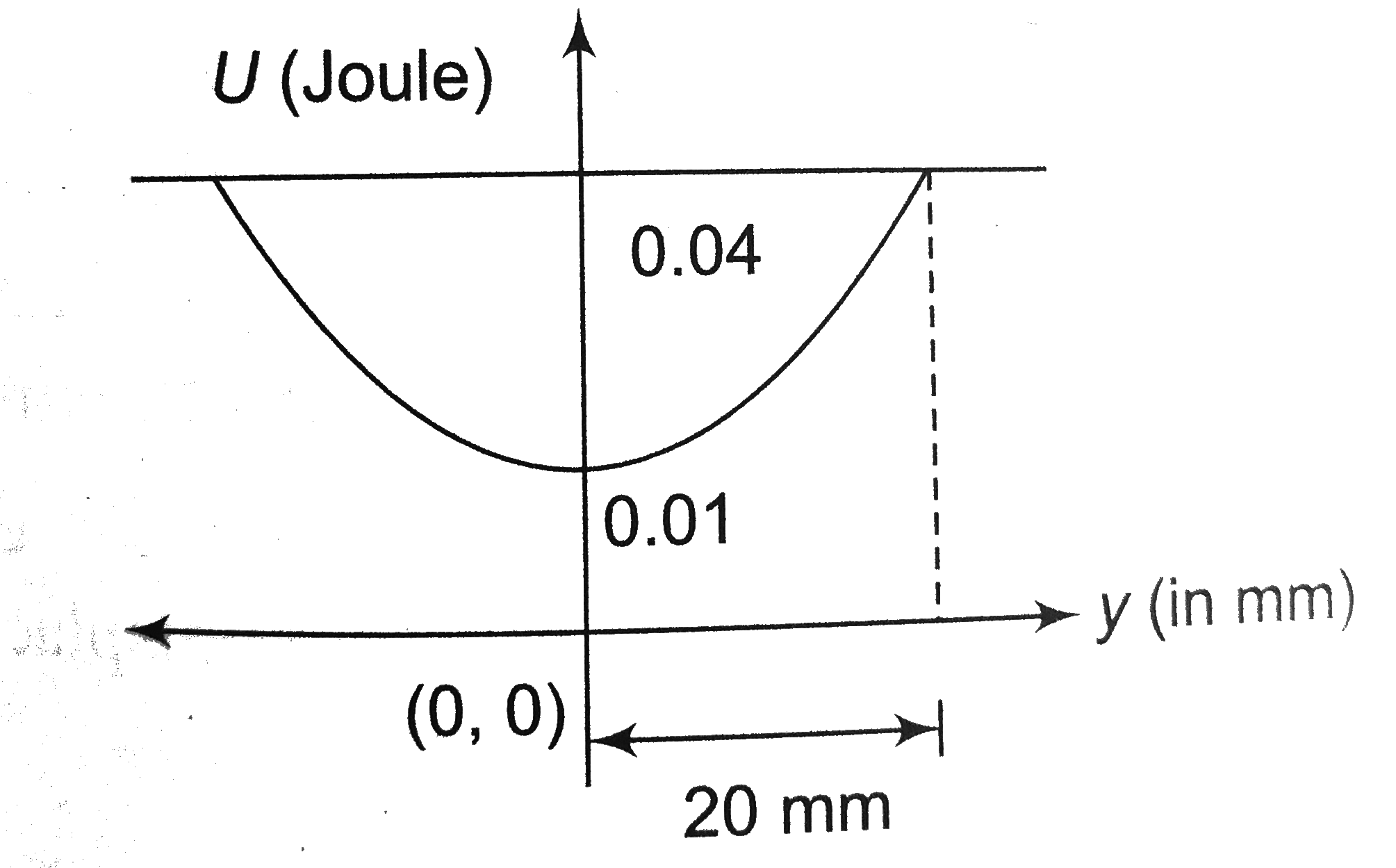
View SolutionThe variation of potential energy of harmonic oscillator is as shown in figure. The spring constant is
View SolutionWhat is the ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator?
View SolutionWhich of the following statements is/are true for a simple harmonic oscillator ?
View Solution