A wire of length 50cm and cross sectional area of 1 sq. mm is extended by 1mm. The required work will be (Y=2×1010Nm−2)
6×10−2J
4×10−2J
2×10−2J
1×10−2J
The correct Answer is:C
To solve the problem, we need to calculate the work done in extending a wire using the given parameters. Here is a step-by-step solution:
Step 1: Identify the given values
- Length of the wire, L=50cm=50×10−2m
- Cross-sectional area, A=1mm2=1×10−6m2
- Extension of the wire, ΔL=1mm=1×10−3m
- Young's modulus, Y=2×1010N/m2
Step 2: Calculate the stress
Stress (σ) is defined as force (F) per unit area (A):
σ=FA
From Young's modulus, we have:
Y=σϵ
where ϵ is the strain, defined as:
ϵ=ΔLL
Thus, we can express stress in terms of Young's modulus and strain:
σ=Y⋅ϵ
Step 3: Calculate the strain
Using the values:
ϵ=ΔLL=1×10−350×10−2=1×10−30.5=2×10−3
Step 4: Calculate the stress
Now substituting the strain into the stress formula:
σ=Y⋅ϵ=2×1010⋅2×10−3=4×107N/m2
Step 5: Calculate the work done
The work done (W) in stretching the wire can be calculated using the formula:
W=12⋅σ⋅ϵ⋅V
where V is the volume of the wire given by:
V=A⋅L
Substituting for V:
V=(1×10−6)⋅(50×10−2)=5×10−6m3
Now substituting σ, ϵ, and V into the work done formula:
W=12⋅(4×107)⋅(2×10−3)⋅(5×10−6)
Step 6: Calculate the final work done
Calculating this gives:
W=12⋅4⋅2⋅5⋅107⋅10−3⋅10−6=12⋅40⋅10−2=20×10−2=2×10−2J
Final Answer
Thus, the required work done is:
W=2×10−2J
---
- Length of the wire, L=50cm=50×10−2m
- Cross-sectional area, A=1mm2=1×10−6m2
- Extension of the wire, ΔL=1mm=1×10−3m
- Young's modulus, Y=2×1010N/m2
Stress (σ) is defined as force (F) per unit area (A):
σ=FA
From Young's modulus, we have:
Y=σϵ
where ϵ is the strain, defined as:
ϵ=ΔLL
Thus, we can express stress in terms of Young's modulus and strain:
σ=Y⋅ϵ
Using the values:
ϵ=ΔLL=1×10−350×10−2=1×10−30.5=2×10−3
Now substituting the strain into the stress formula:
σ=Y⋅ϵ=2×1010⋅2×10−3=4×107N/m2
The work done (W) in stretching the wire can be calculated using the formula:
W=12⋅σ⋅ϵ⋅V
where V is the volume of the wire given by:
V=A⋅L
Substituting for V:
V=(1×10−6)⋅(50×10−2)=5×10−6m3
W=12⋅(4×107)⋅(2×10−3)⋅(5×10−6)
Calculating this gives:
W=12⋅4⋅2⋅5⋅107⋅10−3⋅10−6=12⋅40⋅10−2=20×10−2=2×10−2J
Thus, the required work done is:
W=2×10−2J
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Chapter Exercise
73 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.2
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Calculate the resistance of an aluminium wire of length 50 cmand cross sectional area 2.0mm2. The resistivity of aluminium is (ρ)=2.6×10−8(Ω)m.
View SolutionThe workdone in increasing the length of a one metre long wire of cross − sectional area 1mm2 through 1mm will be (Y=2×1011Nm−2):
View SolutionSpeed of a transverse wave on a straight wire (mass 6 g, length 120 cm and area of cross section 1.2mm2 is 100 m/s) . If the Young's modulus of wire is 1012Nm−2 the extension of wire over its natural length is :
View SolutionSpeed of a transverse wave on a straight wire (mass 6 g, length 120 cm and area of cross section 1.2mm2 is 100 m/s) . If the Young's modulus of wire is 1012Nm−2 the extension of wire over its natural length is :
View SolutionTwo wires of equal length and cross sectional area suspended as shown in
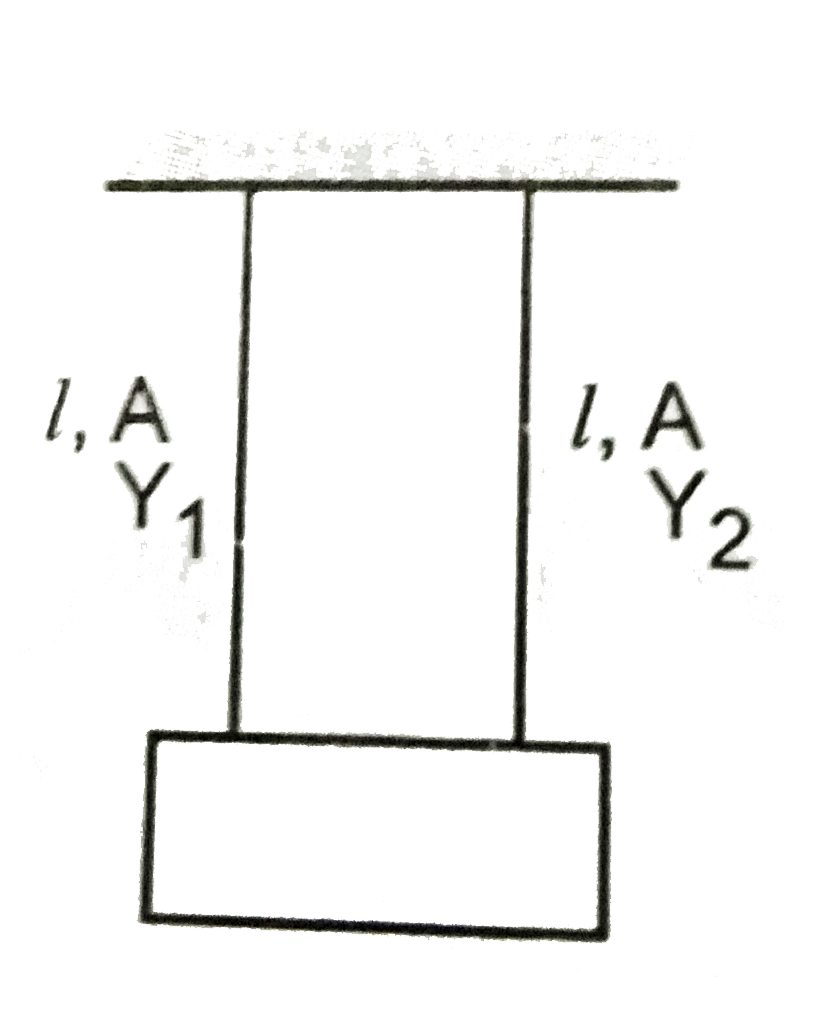
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of equal length and cross sectional area suspended as shown in

Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View SolutionA load of 100 N acts on a bar of length 10 cm and area of cross section 1 cm. Find the energy stored in it. (Y=1011N/m2)
View SolutionA steel wire of 4.0 m is stretched through 2.0 mm. The cross - sectional area of the wire is 2.0mm2. If young's modulus of steel is 2.0×1011Nm−2 find (i) the energy density of the wire, (ii) the elastic potential energy stored in the wire.
View SolutionWhen a force is applied on a wire of uniform cross-sectional area 3×10−6m2 and length 4 m, the increase in length is 1mm. Energy stored in it will be (Y=2×1011Nm2)
View Solution
