If a spring extends by x on loading, then the energy stored by the spring is (if T is tension in the spring and k is spring constant)
T22x
T22K
2xT2
2T22k
The correct Answer is:B
To find the energy stored in a spring when it extends by a distance x, we can use the formula for elastic potential energy stored in a spring, which is derived from Hooke's Law. Here’s the step-by-step solution:
Step 1: Understand Hooke's Law
Hooke's Law states that the force F exerted by a spring is directly proportional to the extension x of the spring from its natural length. Mathematically, it is expressed as:
F=kx
where k is the spring constant.
Step 2: Relate Tension to Extension
In this case, the tension T in the spring can be considered equivalent to the force F applied to the spring when it is extended. Therefore, we can write:
T=kx
Step 3: Calculate the Energy Stored
The energy U stored in the spring when it is extended by x can be calculated using the formula for elastic potential energy:
U=12Fx
Substituting F with T (since T=kx):
U=12Tx
Step 4: Substitute for x
From the relationship T=kx, we can express x in terms of T:
x=Tk
Now substitute this expression for x back into the energy formula:
U=12T(Tk)
This simplifies to:
U=T22k
Conclusion
Thus, the energy stored in the spring when it extends by x is given by:
U=T22k
Hooke's Law states that the force F exerted by a spring is directly proportional to the extension x of the spring from its natural length. Mathematically, it is expressed as:
F=kx
where k is the spring constant.
In this case, the tension T in the spring can be considered equivalent to the force F applied to the spring when it is extended. Therefore, we can write:
T=kx
The energy U stored in the spring when it is extended by x can be calculated using the formula for elastic potential energy:
U=12Fx
Substituting F with T (since T=kx):
U=12Tx
From the relationship T=kx, we can express x in terms of T:
x=Tk
Now substitute this expression for x back into the energy formula:
U=12T(Tk)
This simplifies to:
U=T22k
Thus, the energy stored in the spring when it extends by x is given by:
U=T22k
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Chapter Exercise
73 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.2
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Knowledge Check
A spring is stretched by applying a load to its free end. The strain produced in the spring is
AvolumetricBshearClongitudinal and shearDlongitudinal.
Force constants K1andK2 of two springs are in the ratio 5:4. They are stretched by same length. If potential energy stored in one spring is 25 J then potential energy stored in second spring is
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View SolutionThe pointer reading versus load graph for a spring balance is as shown in the figure.
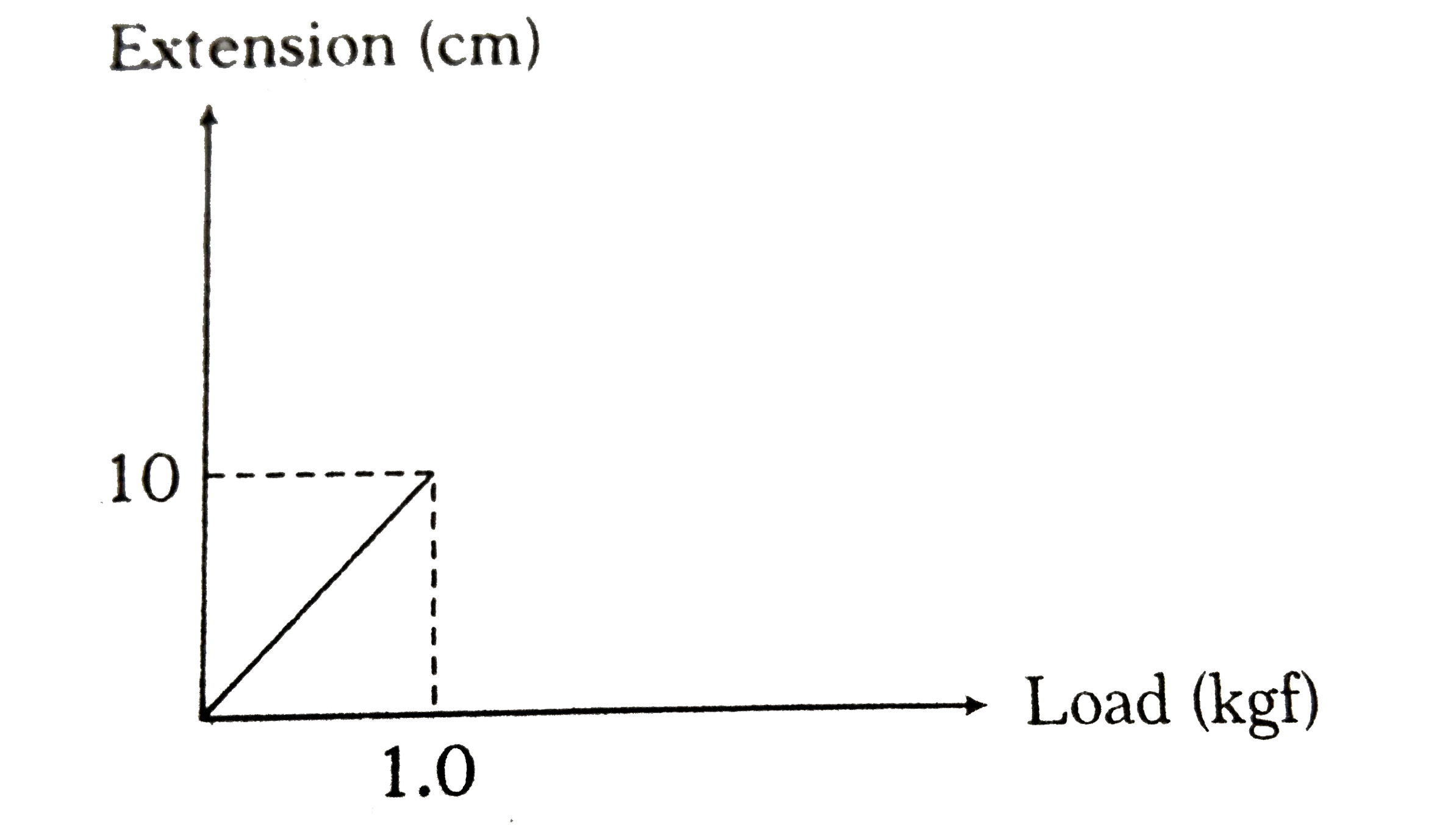
The spring constant is
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View SolutionA spring is stretched by applying a load to its free end. The strain produced in the spring is
View SolutionThe electrical analog of a spring constant k is
View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
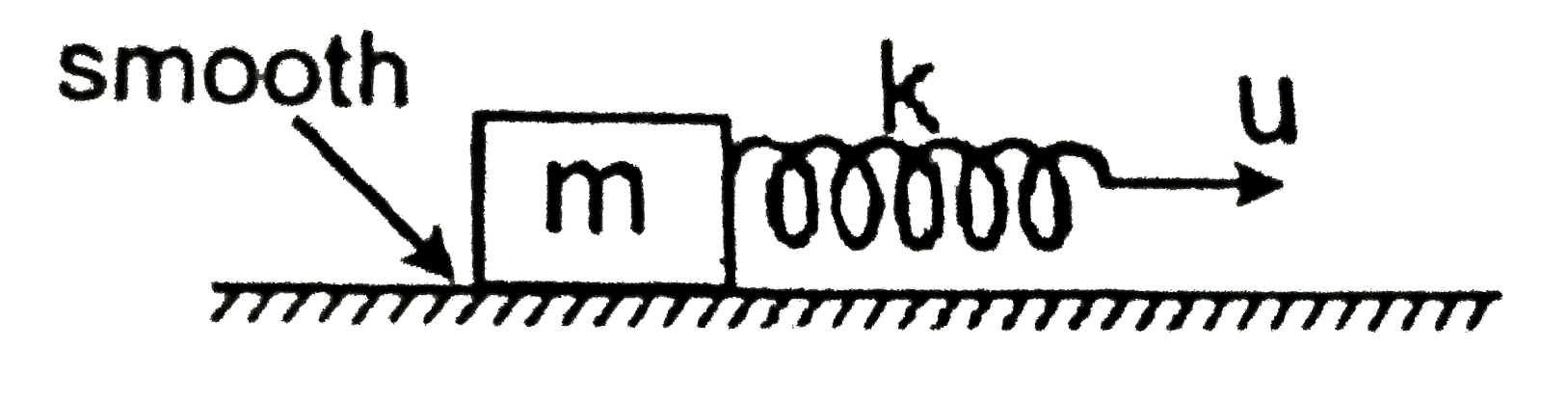
View Solution

