Assertion Upto elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed.
Reason Within elastic limit, the wire follows Hooke's law.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If both Assertion and Reason are false.
The correct Answer is:C
To solve the question, we need to analyze both the assertion and the reason provided, and determine their validity based on the principles of elasticity and Hooke's law.
1. Understanding the Assertion:
- The assertion states that "up to the elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed."
- This is true. When a material is stressed within its elastic limit, it can return to its original shape and dimensions once the stress is removed.
2. Understanding the Reason:
- The reason states that "within the elastic limit, the wire follows Hooke's law."
- Hooke's law states that the strain in a material is directly proportional to the applied stress, provided the material's elastic limit is not exceeded. However, it is important to note that Hooke's law is strictly valid only up to the proportional limit (point A in the stress-strain curve). Beyond this point, the relationship may not hold true, even within the elastic limit.
3. Analyzing the Stress-Strain Curve:
- In a typical stress-strain curve, the initial linear portion (from point O to point A) represents the region where Hooke's law is valid.
- The region from point A to point B is still elastic but does not strictly follow Hooke's law, as the relationship between stress and strain may become non-linear.
4. Conclusion:
- The assertion is true because materials regain their original shape within the elastic limit.
- The reason is false because Hooke's law is only valid up to the proportional limit (point A) and not throughout the entire elastic limit (up to point B).
5. Final Answer:
- The assertion is true, and the reason is false. Therefore, the correct option is that the assertion is true and the reason is false.
- The assertion states that "up to the elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed."
- This is true. When a material is stressed within its elastic limit, it can return to its original shape and dimensions once the stress is removed.
- The reason states that "within the elastic limit, the wire follows Hooke's law."
- Hooke's law states that the strain in a material is directly proportional to the applied stress, provided the material's elastic limit is not exceeded. However, it is important to note that Hooke's law is strictly valid only up to the proportional limit (point A in the stress-strain curve). Beyond this point, the relationship may not hold true, even within the elastic limit.
- In a typical stress-strain curve, the initial linear portion (from point O to point A) represents the region where Hooke's law is valid.
- The region from point A to point B is still elastic but does not strictly follow Hooke's law, as the relationship between stress and strain may become non-linear.
- The assertion is true because materials regain their original shape within the elastic limit.
- The reason is false because Hooke's law is only valid up to the proportional limit (point A) and not throughout the entire elastic limit (up to point B).
- The assertion is true, and the reason is false. Therefore, the correct option is that the assertion is true and the reason is false.
Similar Questions
Assertion Upto the elastic limit, strain ∝ stress.
Reason Upto elastic limit, material returns to its original shape and size, when external force is removed.
View Solution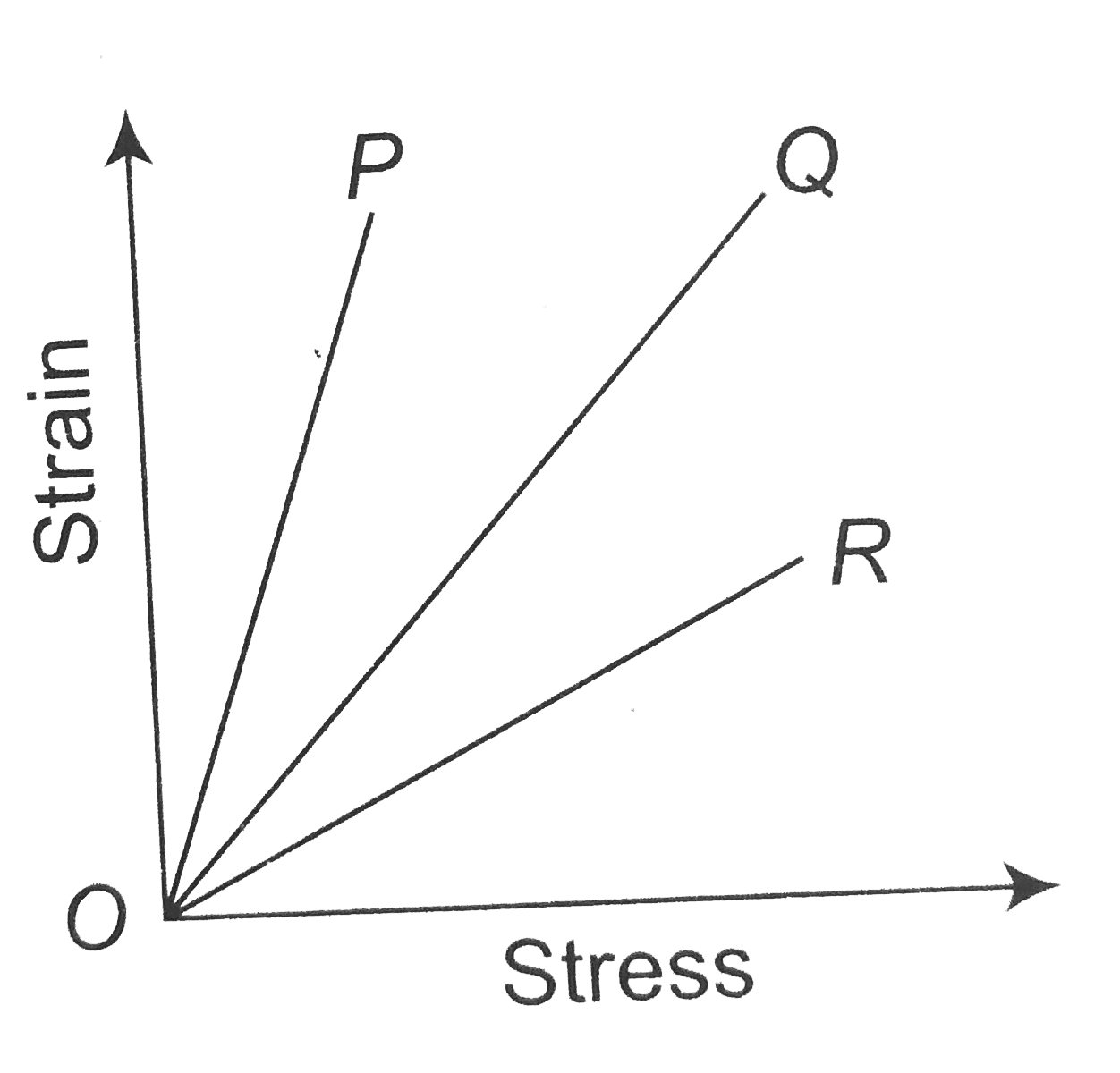
The strain stress curves of three wires of different materials are shown in the figure. P, Q and R are the elastic limits of the wires. The figure shown that
View Solution
Knowledge Check
According to Hooke's law of elasticity, if stress is increaed, the ratio of stress to strain
AdecreasesBincreasesCbecomes zeroDremains constant
Assertion : The materials which have very small range of plastic extension are called brittle material.
Reason: If the stress is increased beyond the elastic limit, the material will break.
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
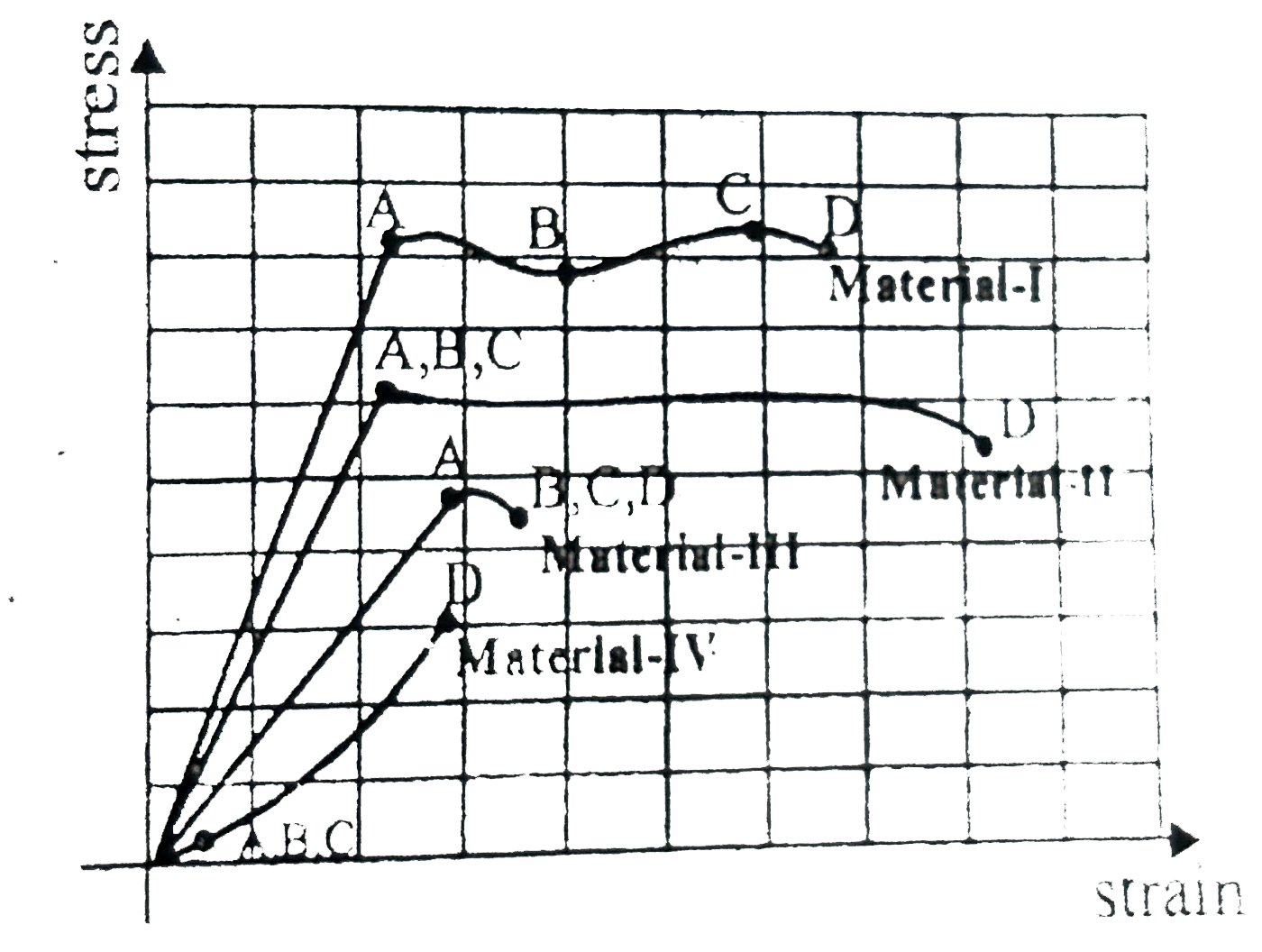
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionWithin the elastic limit, stress is directly proportional to strain produced in a body is the statement of
View SolutionAssertion Stress and modulus of elasticity have the same dimensions
Reason Strain is dimensionless.
View Solution
