A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are . The height of the block above the mercury level is given by
The correct Answer is:B
To solve the problem of finding the height of a cubical block of steel floating on mercury, we can follow these steps:
Step 1: Understand the Problem
We have a cubical block of steel with each side equal to 1 meter, floating in mercury. We need to find the height h of the block that is above the mercury level. The density of steel is ρs and the density of mercury is ρm.
Step 2: Define the Variables
Let:
- The total height of the block = 1 meter
- The height of the block submerged in mercury = 1−h
- The height of the block above the mercury level = h
Step 3: Apply the Principle of Buoyancy
According to Archimedes' principle, the buoyant force acting on the block is equal to the weight of the liquid displaced by the submerged part of the block.
The buoyant force Fb can be expressed as:
Fb=(density of mercury)×(volume submerged)×g
Where:
- Density of mercury = ρm
- Volume submerged = (1−h)×12=1−h (since the area of the base is 1m2)
- g is the acceleration due to gravity (which will cancel out later)
Thus, the buoyant force becomes:
Fb=ρm(1−h)g
Step 4: Calculate the Weight of the Block
The weight W of the block can be expressed as:
W=(density of steel)×(volume of the block)×g
Where:
- Density of steel = ρs
- Volume of the block = 13=1m3
Thus, the weight of the block becomes:
W=ρs⋅1⋅g=ρsg
Step 5: Set Up the Equation
For the block to be in equilibrium (floating), the buoyant force must equal the weight of the block:
ρm(1−h)g=ρsg
Step 6: Simplify the Equation
We can cancel g from both sides:
ρm(1−h)=ρs
Step 7: Solve for h
Rearranging the equation gives:
ρm−ρmh=ρs
ρmh=ρm−ρs
h=ρm−ρsρm
Step 8: Final Expression for Height Above Mercury Level
Now we can express h in a more convenient form:
h=1−ρsρm
Conclusion
The height of the block above the mercury level is given by:
h=1−ρsρm
We have a cubical block of steel with each side equal to 1 meter, floating in mercury. We need to find the height h of the block that is above the mercury level. The density of steel is ρs and the density of mercury is ρm.
Let:
- The total height of the block = 1 meter
- The height of the block submerged in mercury = 1−h
- The height of the block above the mercury level = h
According to Archimedes' principle, the buoyant force acting on the block is equal to the weight of the liquid displaced by the submerged part of the block.
Fb=(density of mercury)×(volume submerged)×g
Where:
- Density of mercury = ρm
- Volume submerged = (1−h)×12=1−h (since the area of the base is 1m2)
- g is the acceleration due to gravity (which will cancel out later)
Fb=ρm(1−h)g
The weight W of the block can be expressed as:
W=(density of steel)×(volume of the block)×g
Where:
- Density of steel = ρs
- Volume of the block = 13=1m3
W=ρs⋅1⋅g=ρsg
For the block to be in equilibrium (floating), the buoyant force must equal the weight of the block:
ρm(1−h)g=ρsg
We can cancel g from both sides:
ρm(1−h)=ρs
Rearranging the equation gives:
ρm−ρmh=ρs
ρmh=ρm−ρs
h=ρm−ρsρm
Now we can express h in a more convenient form:
h=1−ρsρm
The height of the block above the mercury level is given by:
h=1−ρsρm
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA cubical block of iron of side13.6cm is floating in mercury in a vessel .Water is poured in the vessel until it just covers the iron block. What is the height of water column? (ρHg=13.6gmcm3, ρFe=7.2gmcm3, ρH_2O=1gmcm3)
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
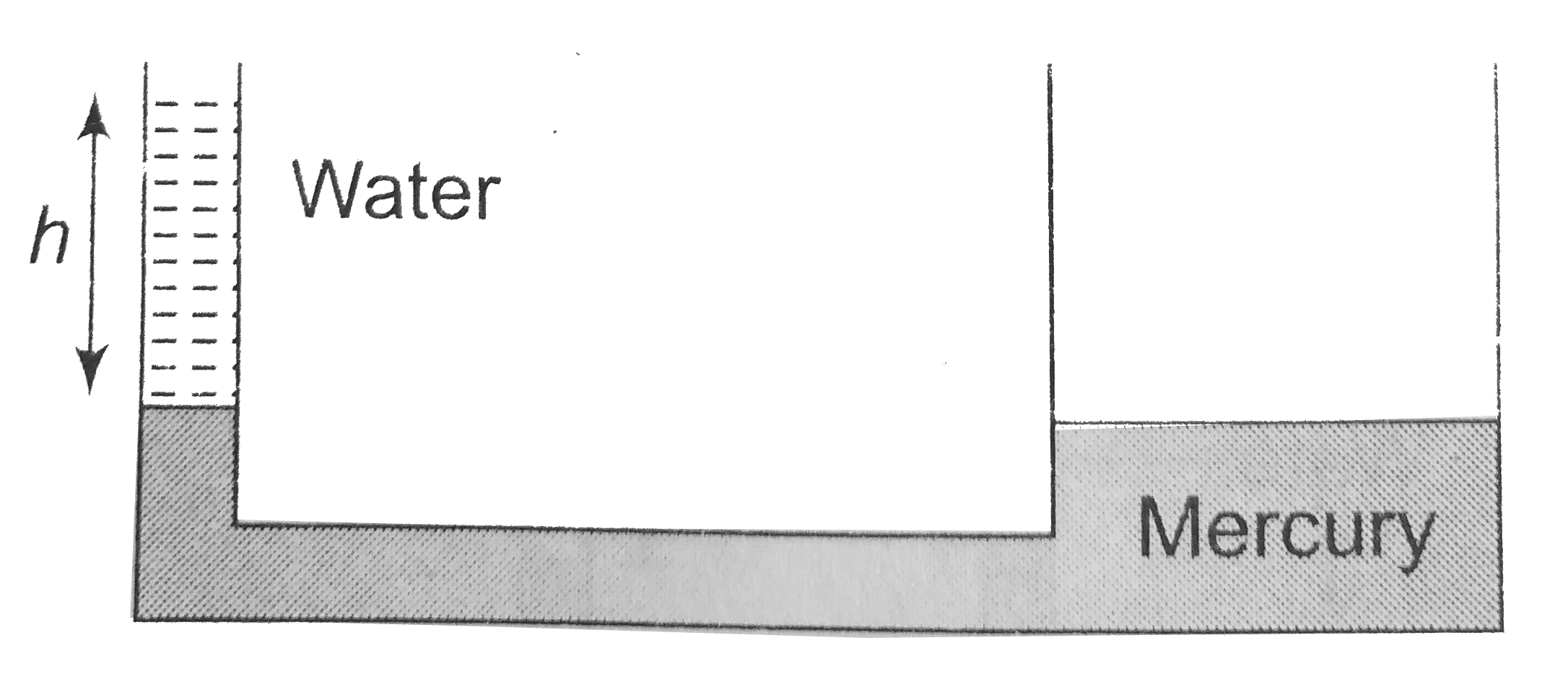
View SolutionTwo communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height 70cm is poured into the narrow vessel. How much wil the mercury level rise in the other vessel and how much will it sink in the narow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is pured into the broad vessel?

View SolutionTwo communicating vessels contain mercury. The diameter of one vessel in n times larger then the diameter of the other. A column of water of height h is poured into the left vessel. The mercury level will rise in the right hand vessel (s = relative density of mercury and ρ = density of water) by
View SolutionA block of iron floats on mercury. Find the fractionof volume which remains immersed in mercury. (Densities of iron and mercury are 7.8gcm−3 and 13.6gcm−3 respectively).
View Solution
The pressures at A and B in the atmosphere are, respectively,
View SolutionState true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
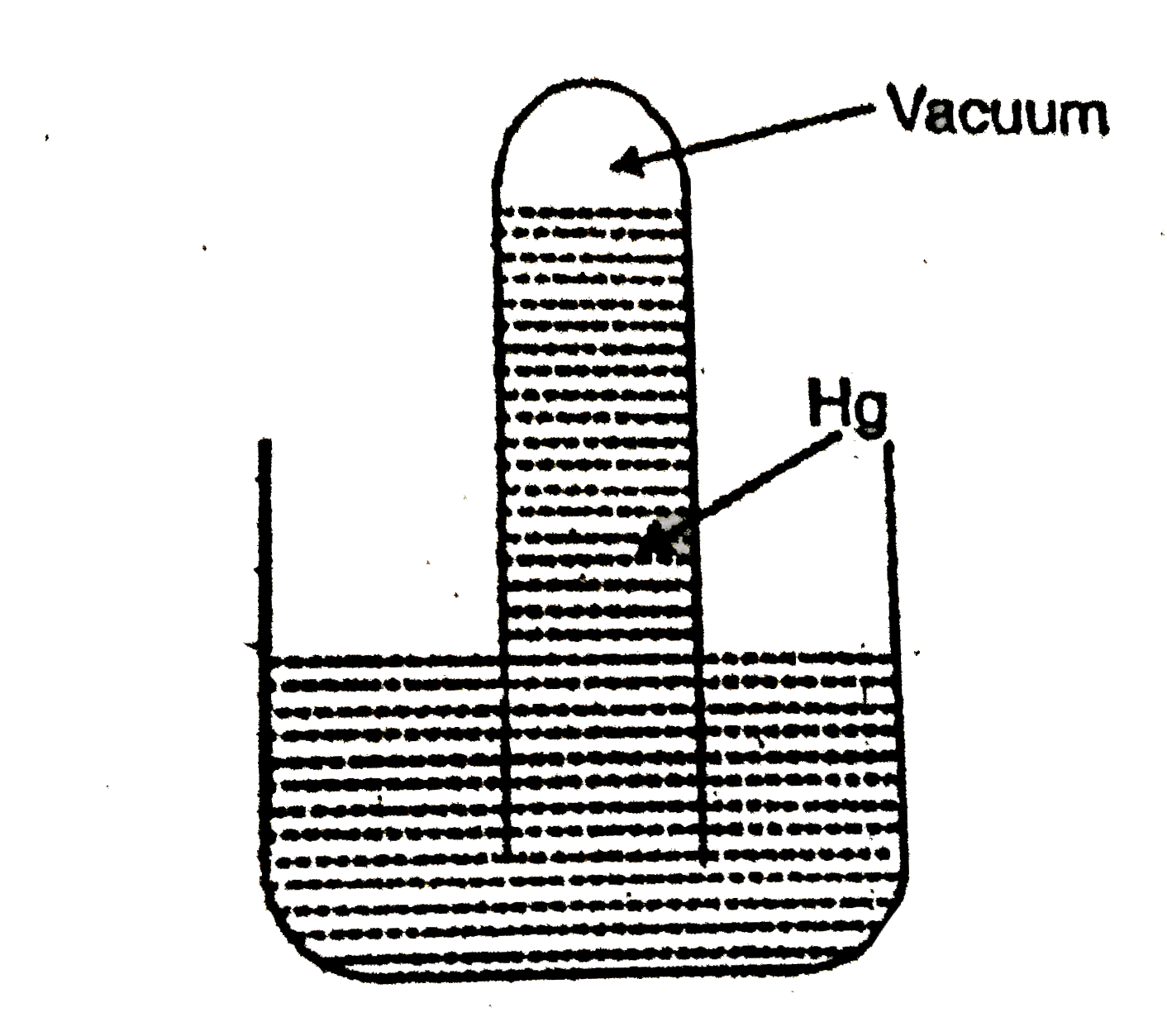
View SolutionThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
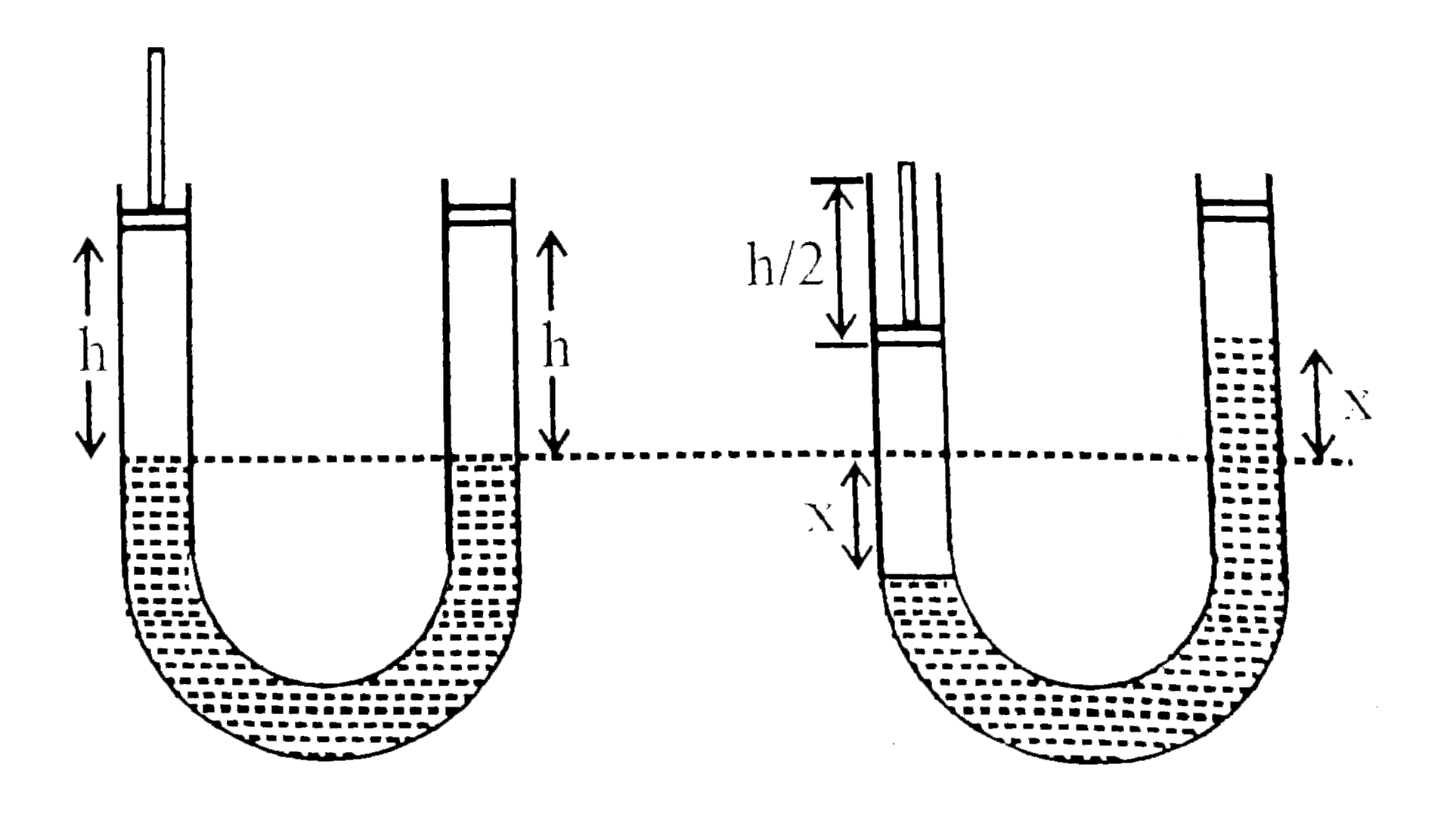
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure then
View Solution
