A small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
σhρ
(σρ−1)h
(1−σhρ)h
ρσ
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the ball and apply the equations of motion to find the height to which the ball will jump above the surface of the liquid.
Step 1: Identify the forces acting on the ball
When the ball is immersed in the liquid, two main forces act on it:
1. The weight of the ball, W=V⋅ρ⋅g, where V is the volume of the ball, ρ is the density of the ball, and g is the acceleration due to gravity.
2. The buoyant force (upthrust) acting on the ball, Fb=V⋅σ⋅g, where σ is the density of the liquid.
Step 2: Calculate the net downward force
The net downward force Fnet acting on the ball can be expressed as:
Fnet=W−Fb=V⋅ρ⋅g−V⋅σ⋅g
This simplifies to:
Fnet=V⋅g(ρ−σ)
Step 3: Determine the net acceleration of the ball
Using Newton's second law, the net acceleration a of the ball can be calculated as:
a=Fnetm=V⋅g(ρ−σ)V⋅ρ=g(ρ−σ)ρ
Step 4: Calculate the velocity of the ball just before it hits the surface of the liquid
When the ball is released from a depth h, we can use the kinematic equation:
v2=u2+2ah
Here, the initial velocity u=0 (since it is released), so:
v2=0+2⋅a⋅h=2⋅(g(ρ−σ)ρ)⋅h
Thus:
v2=2g(ρ−σ)ρ⋅h
Step 5: Apply the equation of motion for the jump above the surface
When the ball reaches the surface of the liquid, it will jump to a height ha in the air. At the maximum height, the final velocity is 0. Using the equation:
0=v2−2gha
We can substitute for v2:
0=2g(ρ−σ)ρ⋅h−2gha
Rearranging gives:
2gha=2g(ρ−σ)ρ⋅h
Dividing both sides by 2g:
ha=(ρ−σ)ρ⋅h
Step 6: Final expression for the height above the surface
To express the height ha in terms of σ and ρ:
ha=(σ−ρρ)⋅h
Thus, the height above the surface of the liquid to which the ball will jump is:
ha=(σ−ρρ)⋅h
When the ball is immersed in the liquid, two main forces act on it:
1. The weight of the ball, W=V⋅ρ⋅g, where V is the volume of the ball, ρ is the density of the ball, and g is the acceleration due to gravity.
2. The buoyant force (upthrust) acting on the ball, Fb=V⋅σ⋅g, where σ is the density of the liquid.
The net downward force Fnet acting on the ball can be expressed as:
Fnet=W−Fb=V⋅ρ⋅g−V⋅σ⋅g
This simplifies to:
Fnet=V⋅g(ρ−σ)
Using Newton's second law, the net acceleration a of the ball can be calculated as:
a=Fnetm=V⋅g(ρ−σ)V⋅ρ=g(ρ−σ)ρ
When the ball is released from a depth h, we can use the kinematic equation:
v2=u2+2ah
Here, the initial velocity u=0 (since it is released), so:
v2=0+2⋅a⋅h=2⋅(g(ρ−σ)ρ)⋅h
Thus:
v2=2g(ρ−σ)ρ⋅h
When the ball reaches the surface of the liquid, it will jump to a height ha in the air. At the maximum height, the final velocity is 0. Using the equation:
0=v2−2gha
We can substitute for v2:
0=2g(ρ−σ)ρ⋅h−2gha
Rearranging gives:
2gha=2g(ρ−σ)ρ⋅h
Dividing both sides by 2g:
ha=(ρ−σ)ρ⋅h
To express the height ha in terms of σ and ρ:
ha=(σ−ρρ)⋅h
ha=(σ−ρρ)⋅h
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question19videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns6videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.410videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View Solution
Knowledge Check
- Question 1 - Select One
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A wooden ball of density D is immersed in water of density d to a depth h//2 below the surface of water and then relased. To what height will the ball jump out of water ?
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA ball of radius r and density ρ is moving in a liquid of density σ1 and then in a liquid of density simga3. The velocity of the ball remains same in all the three liquids. (Givenσ3>σ2>σ1). If n1,n2andn3 are their coefficients of viscosity , then which of the following is always true ?
 View Solution
View SolutionA small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
View SolutionA ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
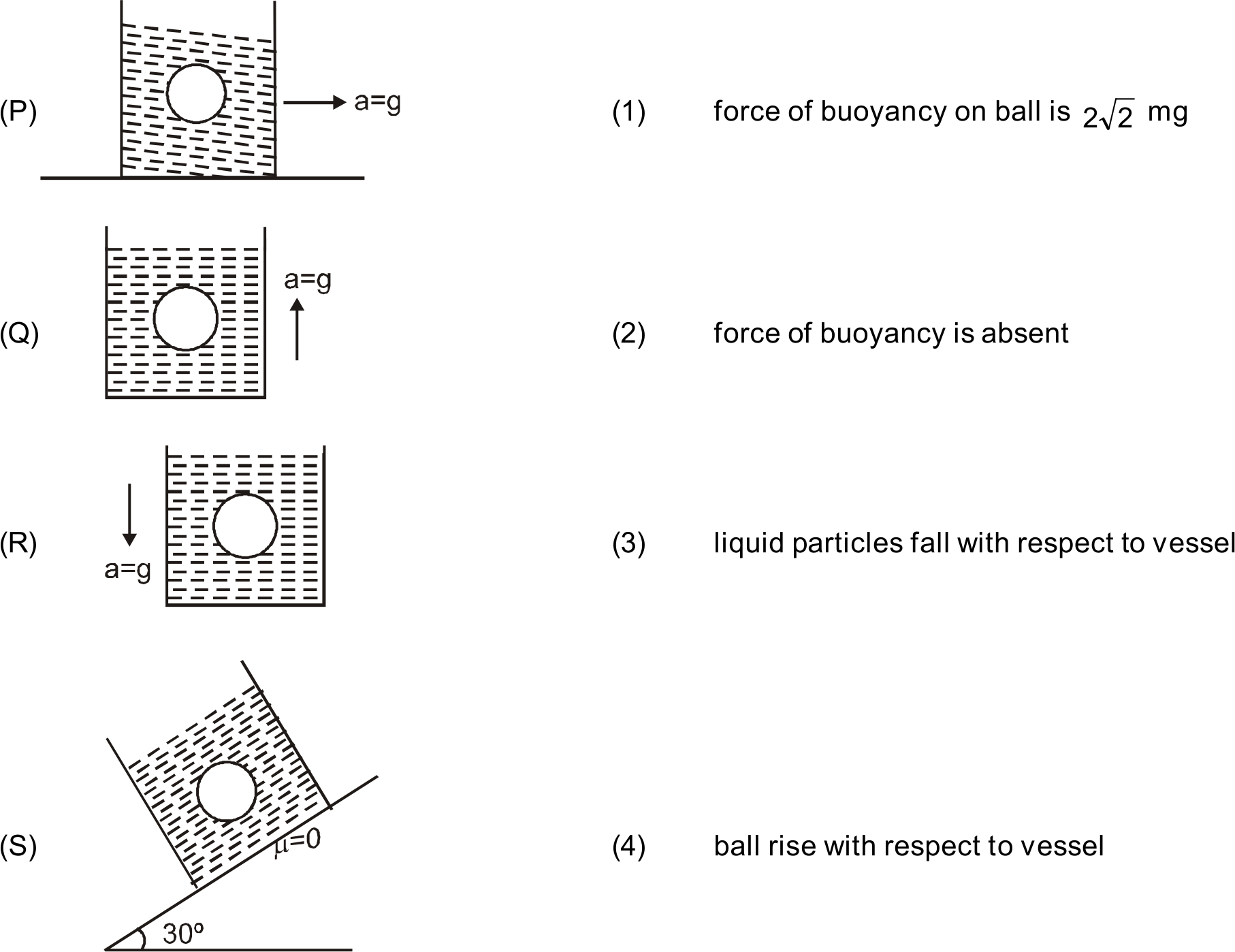 View Solution
View SolutionA body of volume V and desnity ρ is initially submerged in a non-viscous liquid of density σ(>ρ). If it is rises by itself through a height h in the liquid. Its kinetic energy will
View Solution

