An open tank containing non-viscous liquid to a height of 5 m is placed over the ground. A heavy sperical ball falls from height 40 m over the ground which ball will go back. Collision between ball and bottom of tank is perfectly elastic
45 m
35m
40 m
20 m
The correct Answer is:C
To solve the problem, we need to analyze the situation step by step:
Step 1: Understand the setup
We have an open tank filled with a non-viscous liquid (water) to a height of 5 meters. A heavy spherical ball is dropped from a height of 40 meters above the ground. The collision between the ball and the bottom of the tank is perfectly elastic.
Hint: Visualize the setup by sketching the tank and the ball's trajectory.
Step 2: Determine the initial energy of the ball
When the ball is dropped from a height of 40 meters, it possesses gravitational potential energy given by the formula:
PE=mgh
where:
- m = mass of the ball
- g = acceleration due to gravity (approximately 9.81m/s2)
- h = height (40 m)
Hint: Remember that potential energy converts to kinetic energy as the ball falls.
Step 3: Calculate the velocity of the ball just before impact
As the ball falls, it converts its potential energy into kinetic energy. Just before hitting the water surface, all potential energy will have converted into kinetic energy:
KE=12mv2
Setting the potential energy equal to the kinetic energy at the moment before impact:
mgh=12mv2
We can cancel m from both sides (assuming m≠0):
gh=12v2
Solving for v:
v=√2gh=√2⋅9.81⋅40
Hint: Use the values of g and h to compute the velocity.
Step 4: Analyze the collision with the water
When the ball hits the water, it will experience a change in medium, but since the collision with the bottom of the tank is perfectly elastic, it will not lose any energy during the collision.
Hint: Recall that in a perfectly elastic collision, the ball retains its kinetic energy.
Step 5: Determine the height the ball will reach after the collision
Since the collision is perfectly elastic, the ball will rebound with the same kinetic energy it had just before hitting the bottom of the tank. Therefore, it will rise back to the same height from which it fell (40 m).
Hint: Use the conservation of energy principle to confirm that the ball will reach the same height.
Conclusion
The ball will go back to a height of 40 meters after the collision with the bottom of the tank.
Final Answer
The ball will rise back to a height of 40 meters.
We have an open tank filled with a non-viscous liquid (water) to a height of 5 meters. A heavy spherical ball is dropped from a height of 40 meters above the ground. The collision between the ball and the bottom of the tank is perfectly elastic.
When the ball is dropped from a height of 40 meters, it possesses gravitational potential energy given by the formula:
PE=mgh
where:
- m = mass of the ball
- g = acceleration due to gravity (approximately 9.81m/s2)
- h = height (40 m)
As the ball falls, it converts its potential energy into kinetic energy. Just before hitting the water surface, all potential energy will have converted into kinetic energy:
KE=12mv2
Setting the potential energy equal to the kinetic energy at the moment before impact:
mgh=12mv2
We can cancel m from both sides (assuming m≠0):
gh=12v2
Solving for v:
v=√2gh=√2⋅9.81⋅40
When the ball hits the water, it will experience a change in medium, but since the collision with the bottom of the tank is perfectly elastic, it will not lose any energy during the collision.
Since the collision is perfectly elastic, the ball will rebound with the same kinetic energy it had just before hitting the bottom of the tank. Therefore, it will rise back to the same height from which it fell (40 m).
The ball will go back to a height of 40 meters after the collision with the bottom of the tank.
The ball will rise back to a height of 40 meters.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
View SolutionA steel ball is dropped from the roof of a building .An observer standing in front of a window 1.25 m high notes that the ball takes 1/8 s to fall from the top to the bottom of the window .The ball reappears at the bottom of the window 2s after passing it on the way down,if the collision between the ball reappears at the bottom of the window 2s after passing it on the way down.If the collision between the ball and the ground is perfectly elastic,then find the height of the building?Take g=10 m/s2.
View SolutionA tennis ball with (small) mass m2 rests on the top of a basketball of mass m1which is at a height h above the ground, and the bottom of the tennis ball is at height h+d above the ground. The balls are dropped. To what height does the tennis ball bounce with respect to ground? (Assume all collisions to be elastic and m1>>m2)
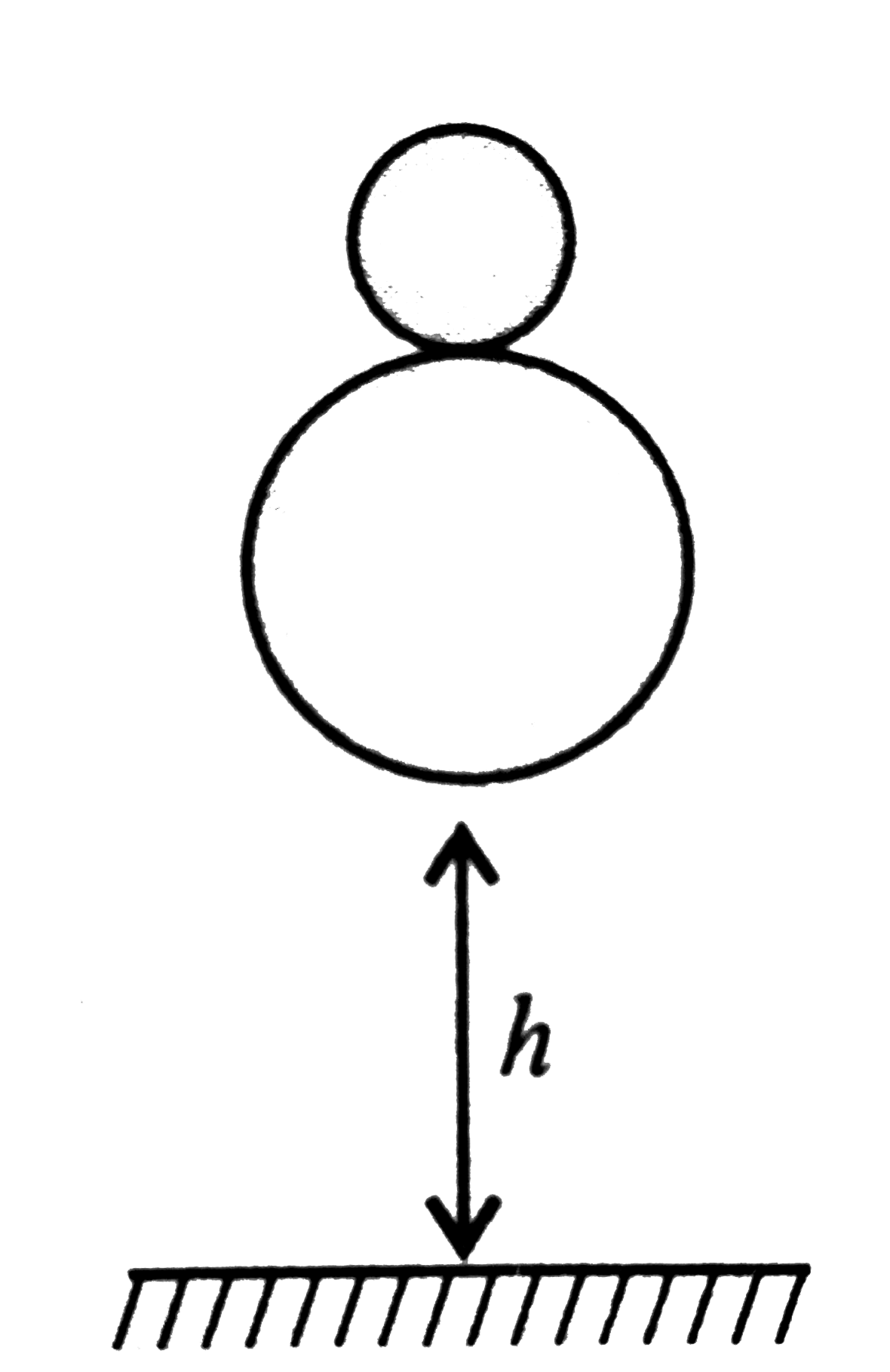
View SolutionA metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
View SolutionA ball is dropped on the ground from a height 10 m. If coefficient of restitution f 0.4, then find the height of which ball will rebound.
View SolutionA ball is allowed to fall from a height of 10m . If there is 40% loss of energy due to impact, then after one impact ball will go up to
View SolutionA ball of relative density 0.8 falls into water from a height of 2 m. The depth to which the ball will sink is (neglect viscous forces)
View SolutionA ball dropped from a height of 2 m rebounds to a height of 1.5 m after hitting the ground. Then fraction of energy lost is
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionA tank is filled up to a height 2H with a liquid and is placed on a platform of height H from the ground, the distance x from the ground where a small hole is punched to get the maximum range R is
 .
.
View Solution
