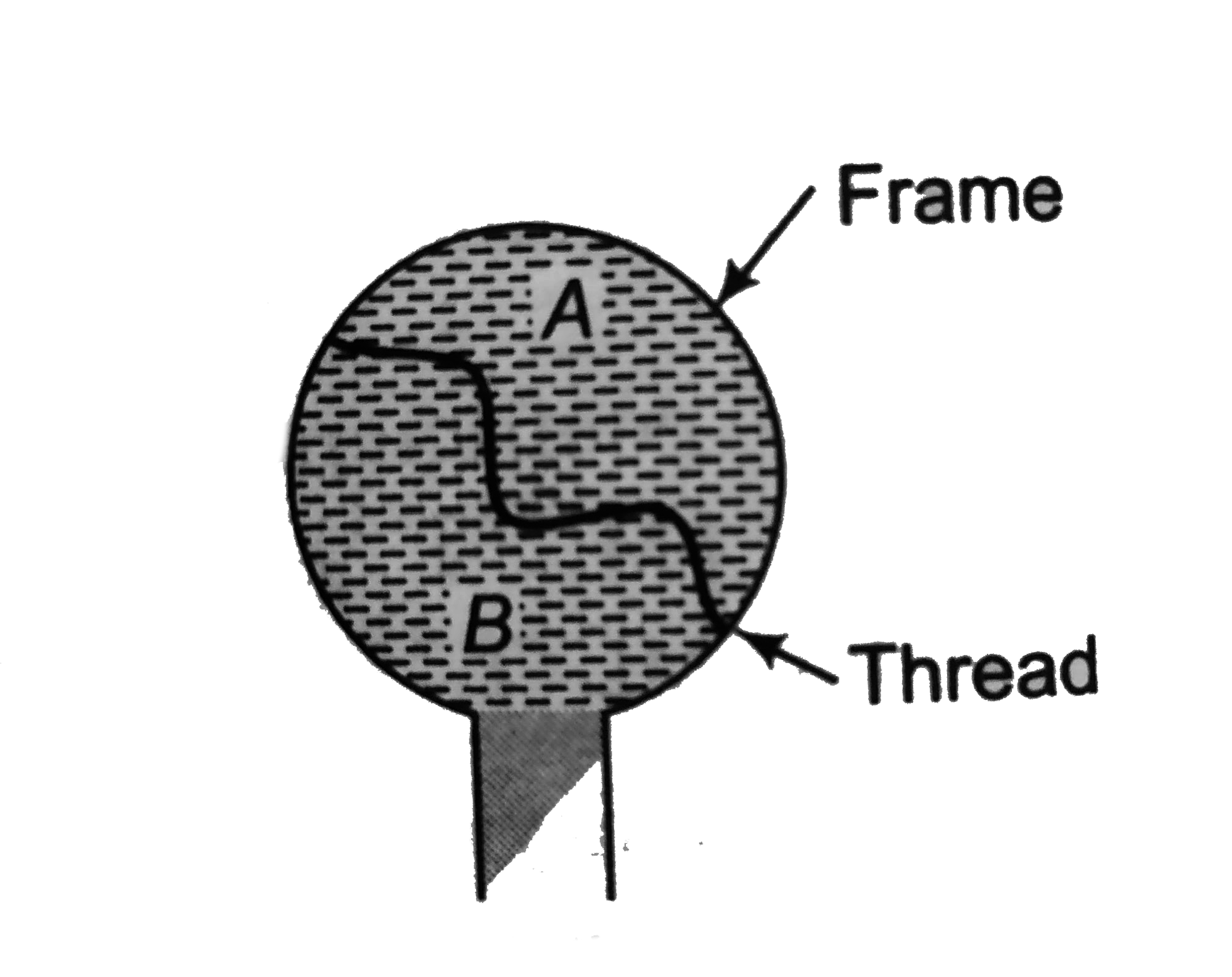
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out. The frame is completely covered with the film. When the portion A is punctured with a pin, the thread
 .
.
thread will become concave on seeing from side A
thread will become concave on seeing from side B
thread will become straight
thread will remain as it is
The correct Answer is:A
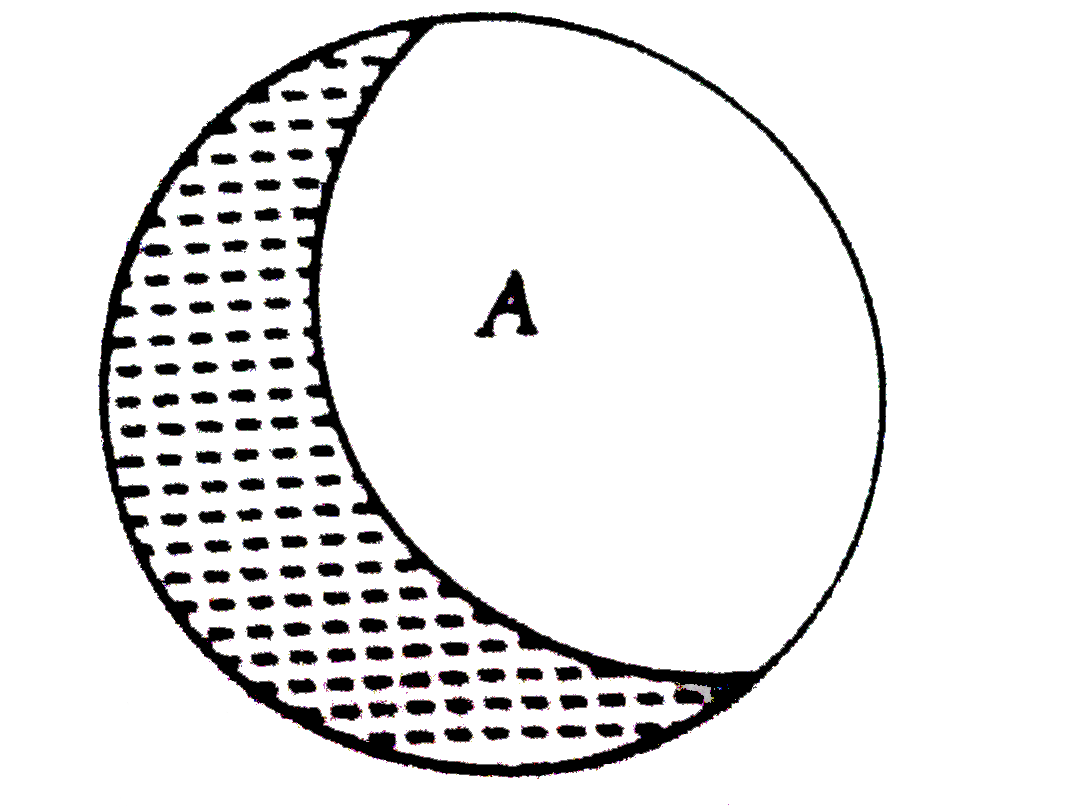
B will keep its area as minimum as possible.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
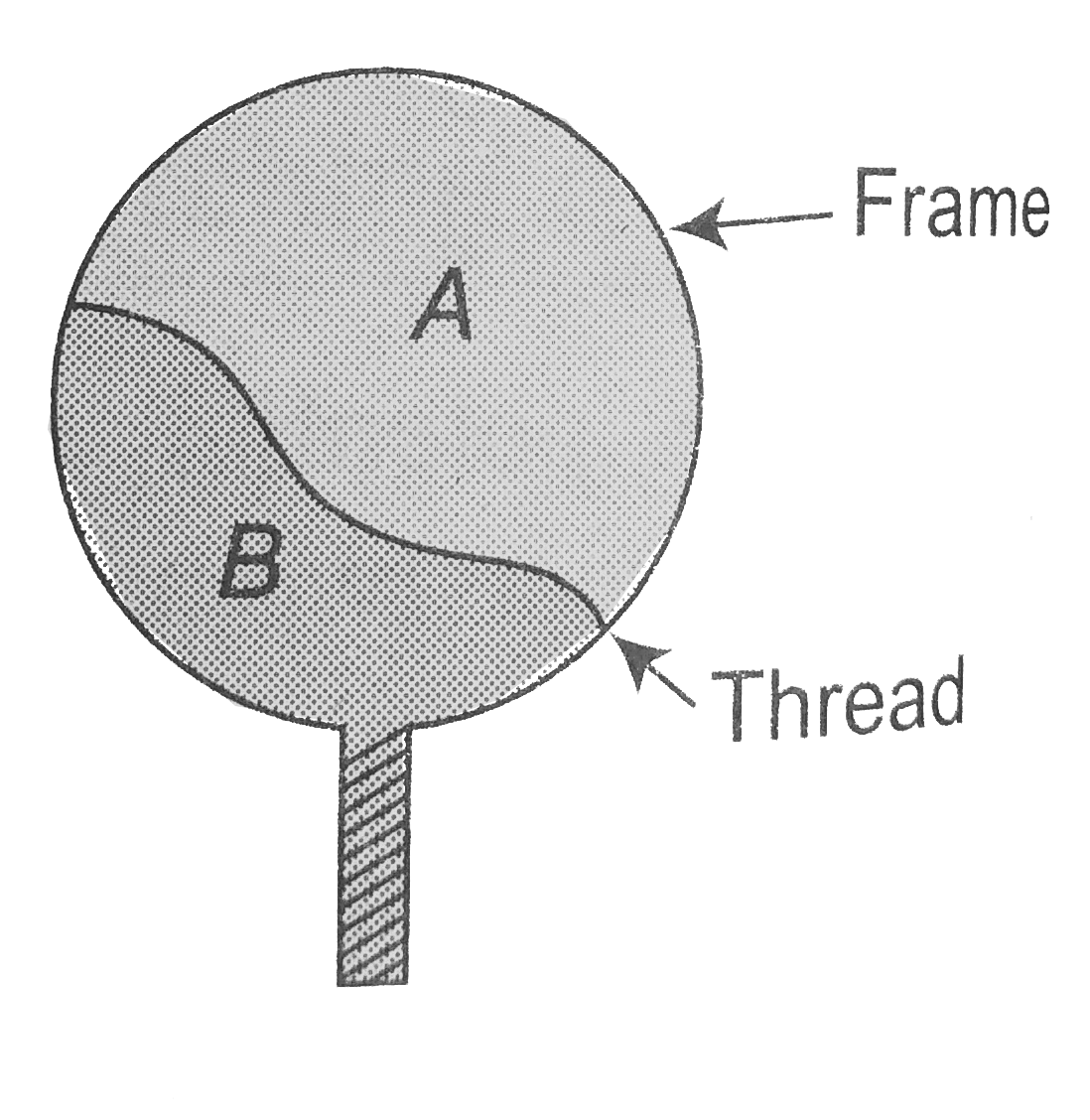
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out . The frame is comletely covered with the film. When the portion A puntured with a pin The thread.
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

View Solution
Knowledge Check
A square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
A2 T LB4 T LC8 T LD10 T L
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25 dyne cm−1. Take g=10ms−2

View SolutionA square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
View SolutionShows a rod PQ of length 20.0 cm and mass 200g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strenght 0.500 T exists in the vicinity of the wire PQ as shown in the figure. The exists in the vicinity of the wire PQ as shown in the figure. The wires conecting PQ with the battery are loose and exert no force on PQ.(a) find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.

View SolutionConsider a U-shaped frame with a sliding wire of length l and mass 'm' on its arm. It is dipped in a soap solution, taken out and placed in vertical position as shown in figure. Choose minimum value of m so that does not descent (Surface tension of soap solution is S)

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution
