Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
2p0(r3−r31−r32)4(r21+r22−r2)
p0(r3−r31−r32)4(r21+r22−r2)
p0(r3+r21+r32)4(r21+r22+r2)
None of these
The correct Answer is:B
As mass of the air is conserved,
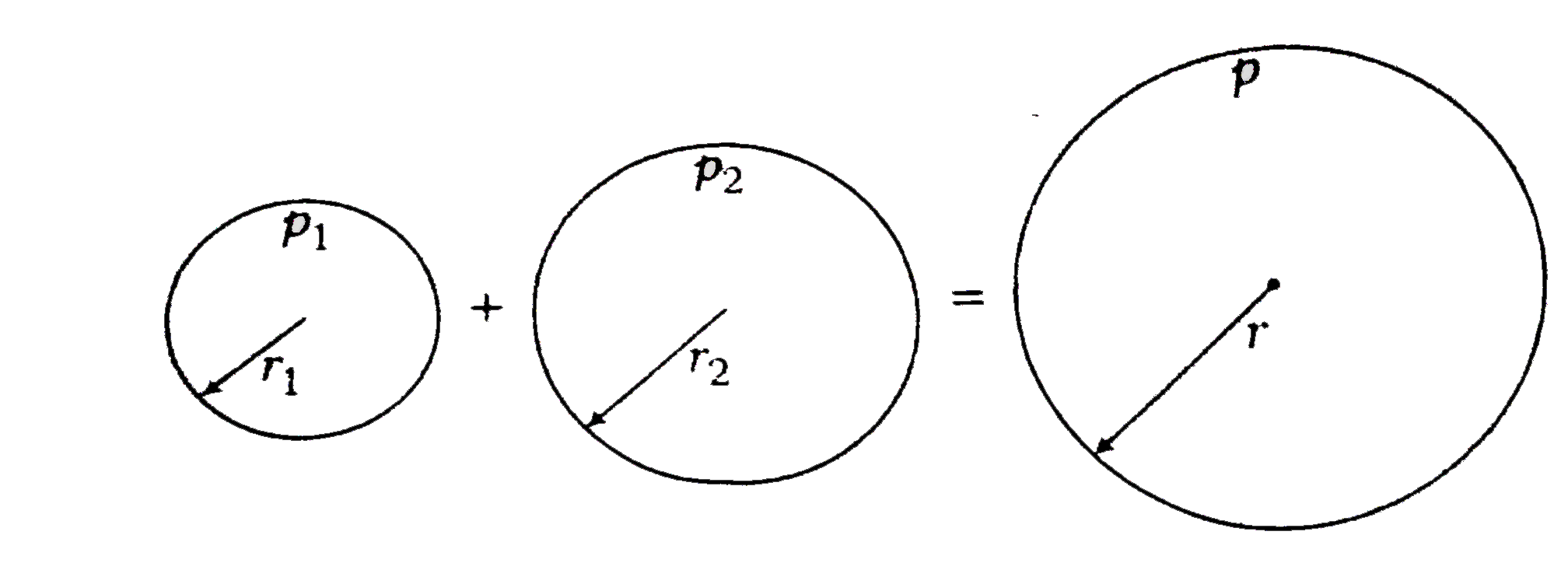
∴ n1+n2=n (aspV=nRT)
∴p1V1RT1+p2V2RT2=pVRT
As temperature is constant,
T1=T2=T
∴p1V1+p2V2=pV
∴(p0+4Sr1)(43πr31)+(p0+4Sr2)(43πr32)=(p0+4Sr)(43πr3)
Solving, this we get
S=p0(r3−r31−r32)4(r1r2+r22−r2)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question19videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns6videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.410videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View Solution
Knowledge Check
- Question 1 - Select One
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2 - Question 2 - Select One
The radii of two soap bubbles are r1andr2(r2<r1). They meet to produce a double bubble. The radius of their common interface is
Ar1r2r1+r2Br1+r22Cr1r2r1−r2Dr2−r1
Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
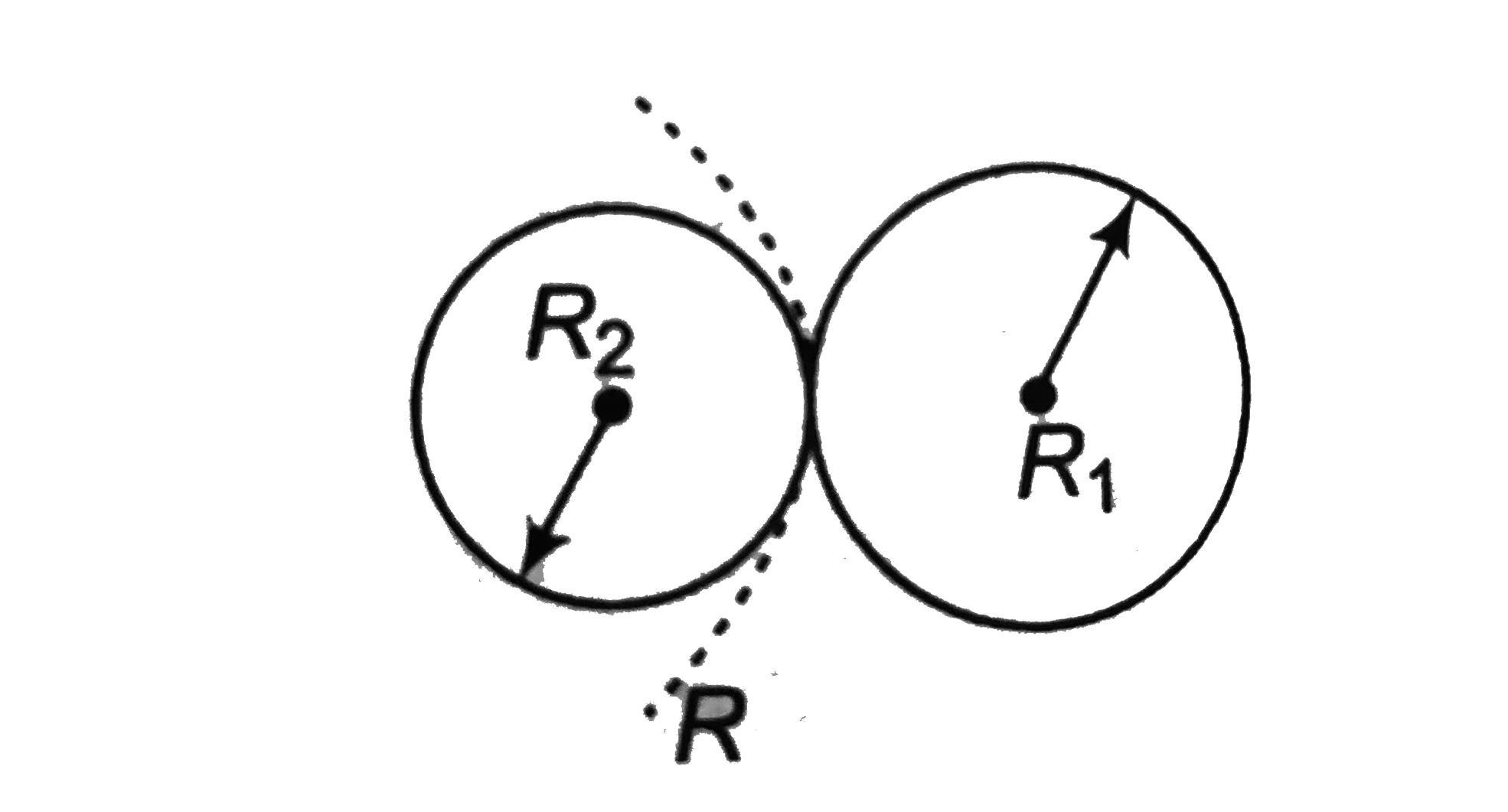 .View Solution
.View SolutionAir is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View SolutionA soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
View SolutionTwo soap bubbles in vacuum of radius 3cm and4cm coalesce to form a single bubble, in same temperature. What will be the radius of the new bubble
View Solution
