Two rods of different materials having coefficient of thermal expansion and young's modulii respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of rods. If , the thermal stresses developed in the two rods are equal provided is equal to
The correct Answer is:C
To solve the problem, we need to find the ratio of the Young's moduli Y1 and Y2 of the two rods given that the thermal stresses developed in both rods are equal. We are given the ratio of their coefficients of thermal expansion α1:α2=2:3.
1. Understanding Thermal Stress:
The thermal stress in a material can be expressed as:
Stress=Y×Strain
where Y is the Young's modulus and the strain is caused by thermal expansion.
2. Expressing Strain:
The strain (ϵ) due to thermal expansion can be expressed as:
ϵ=ΔLL=αΔT
where ΔL is the change in length, L is the original length, α is the coefficient of thermal expansion, and ΔT is the change in temperature.
3. Setting Up the Equations:
For rod 1 (material with Y1 and α1):
Stress1=Y1×ϵ1=Y1×α1ΔT
For rod 2 (material with Y2 and α2):
Stress2=Y2×ϵ2=Y2×α2ΔT
4. Equating the Stresses:
Since the thermal stresses are equal:
Y1α1ΔT=Y2α2ΔT
We can cancel ΔT from both sides (since it is the same for both rods):
Y1α1=Y2α2
5. Finding the Ratio of Young's Moduli:
Rearranging the equation gives:
Y1Y2=α2α1
6. Substituting the Given Ratio:
We know from the problem that:
α1α2=23
Therefore:
α2α1=32
7. Final Ratio of Young's Moduli:
Substituting this back into our equation:
Y1Y2=32
Thus, the required ratio of Young's moduli Y1:Y2 is 3:2.
Final Answer:
Y1:Y2=3:2
The thermal stress in a material can be expressed as:
Stress=Y×Strain
where Y is the Young's modulus and the strain is caused by thermal expansion.
The strain (ϵ) due to thermal expansion can be expressed as:
ϵ=ΔLL=αΔT
where ΔL is the change in length, L is the original length, α is the coefficient of thermal expansion, and ΔT is the change in temperature.
For rod 1 (material with Y1 and α1):
Stress1=Y1×ϵ1=Y1×α1ΔT
For rod 2 (material with Y2 and α2):
Stress2=Y2×ϵ2=Y2×α2ΔT
Since the thermal stresses are equal:
Y1α1ΔT=Y2α2ΔT
We can cancel ΔT from both sides (since it is the same for both rods):
Y1α1=Y2α2
Rearranging the equation gives:
Y1Y2=α2α1
We know from the problem that:
α1α2=23
Therefore:
α2α1=32
Substituting this back into our equation:
Y1Y2=32
Y1:Y2=3:2
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Check point 14.3
Explore 20 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Check point 14.4
Explore 25 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Check point 14.1
Explore 10 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Level 2 Subjective
Explore 8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Level 2 Subjective
Explore 9 Videos
Similar Questions
Two rods of different materials having coefficients of thermal expansion α1, α2 and Young's modulii Y1, Y2 respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If α1:α2=2:3, the thermal stresses developed in the two rods are equal provided Y1:Y2 is equal to
View SolutionTwo rods of different materials having coefficient of thermal expansion α1 and α2 and Young's modulus Y1 and Y2 respectively are fixed between two rigid supports separately. The rods are heated such that they undergo same temperature increment. If thermal stress developed in two rods are equal, then Y1:Y2 is
View SolutionTwo rods of lengths l1andl2 are made of materials having coefficients of linear expansion α1andα2 respectively. What could be the relation between above values, if the difference in the lengths of the two rods does not depends on temperature variation?
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionThere are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
(α1,α2= linear expansion coefficient
A1,A2= Area of rods
Y1,Y2= Young modulus )
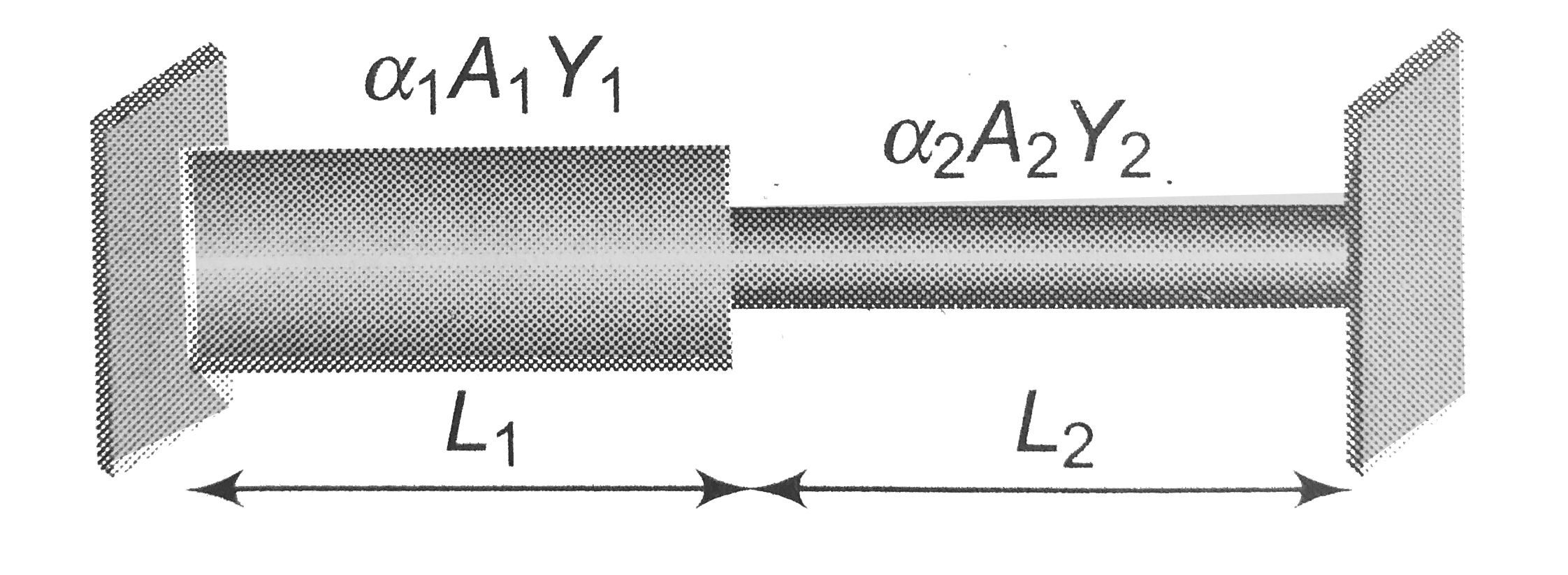
View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
(α1,α2= linear expansion coefficient
A1,A2= Area of rods
Y1,Y2= Young modulus )

View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
(α1,α2= linear expansion coefficient
A1,A2= Area of rods
Y1,Y2= Young modulus )

View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
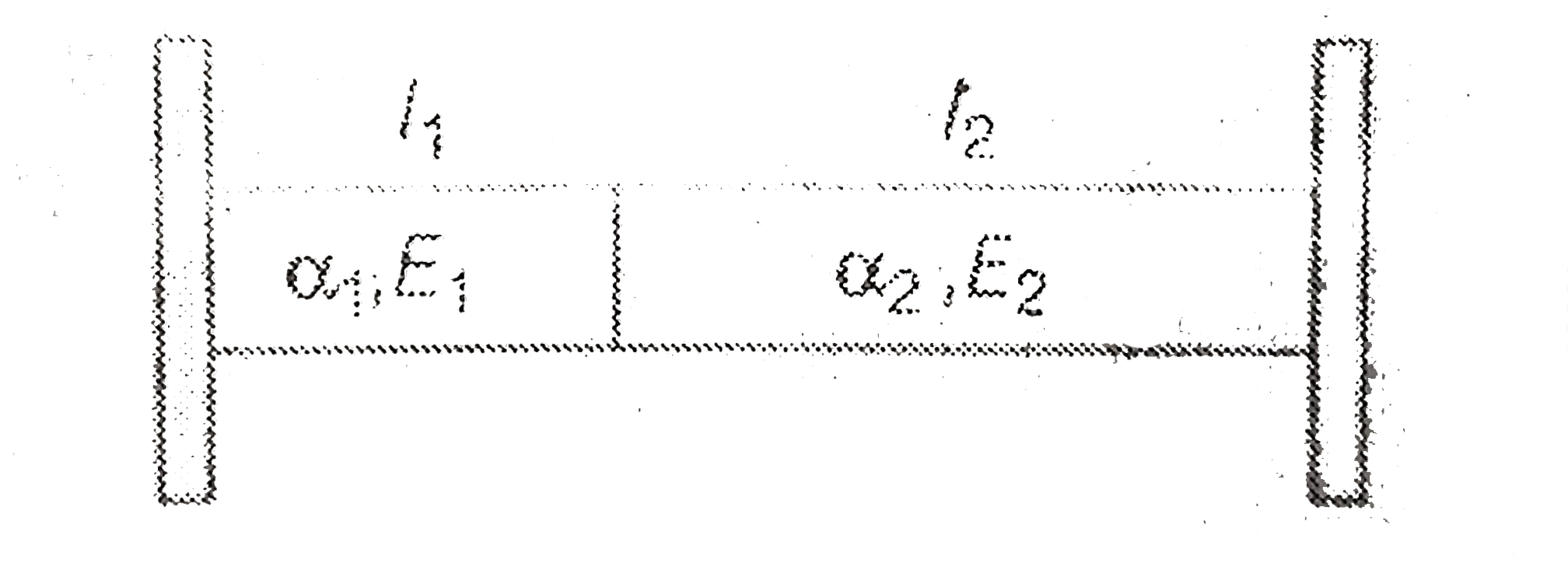
View Solution