Two unifrom brass rod A and B of length l and 2l and radii 2r respectively are heated to the same temperature. The ratio of the increase in the volume of A to that of B is
1:1
1:2
2:1
1:4
The correct Answer is:C
To solve the problem of finding the ratio of the increase in the volume of two brass rods A and B when heated to the same temperature, we will follow these steps:
Step 1: Determine the original volumes of the rods
The volume V of a cylindrical rod is given by the formula:
V=Area×Length
The area A of a circle is given by:
A=πr2
For rod A:
- Length LA=l
- Radius rA=r
Thus, the volume VA of rod A is:
VA=πr2l
For rod B:
- Length LB=2l
- Radius rB=2r
Thus, the volume VB of rod B is:
VB=π(2r)2(2l)=π(4r2)(2l)=8πr2l
Step 2: Calculate the change in volume due to heating
The change in volume ΔV due to thermal expansion is given by:
ΔV=V⋅γ⋅ΔT
where γ is the coefficient of volumetric expansion and ΔT is the change in temperature.
For rod A:
ΔVA=VA⋅γ⋅ΔT=(πr2l)⋅γ⋅ΔT
For rod B:
ΔVB=VB⋅γ⋅ΔT=(8πr2l)⋅γ⋅ΔT
Step 3: Find the ratio of the increases in volume
Now, we will find the ratio of the increase in volume of rod A to that of rod B:
ΔVAΔVB=πr2l⋅γ⋅ΔT8πr2l⋅γ⋅ΔT
The π, r2, l, γ, and ΔT terms cancel out:
ΔVAΔVB=18
Step 4: Final result
Thus, the ratio of the increase in the volume of rod A to that of rod B is:
ΔVAΔVB=18
Conclusion
The ratio of the increase in the volume of rod A to that of rod B is 1:8.
---
The volume V of a cylindrical rod is given by the formula:
V=Area×Length
The area A of a circle is given by:
A=πr2
For rod A:
- Length LA=l
- Radius rA=r
VA=πr2l
- Length LB=2l
- Radius rB=2r
VB=π(2r)2(2l)=π(4r2)(2l)=8πr2l
The change in volume ΔV due to thermal expansion is given by:
ΔV=V⋅γ⋅ΔT
where γ is the coefficient of volumetric expansion and ΔT is the change in temperature.
ΔVA=VA⋅γ⋅ΔT=(πr2l)⋅γ⋅ΔT
ΔVB=VB⋅γ⋅ΔT=(8πr2l)⋅γ⋅ΔT
Now, we will find the ratio of the increase in volume of rod A to that of rod B:
ΔVAΔVB=πr2l⋅γ⋅ΔT8πr2l⋅γ⋅ΔT
ΔVAΔVB=18
Thus, the ratio of the increase in the volume of rod A to that of rod B is:
ΔVAΔVB=18
The ratio of the increase in the volume of rod A to that of rod B is 1:8.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions14videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Match the columns5videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.425videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective8videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective9videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
Similar Questions
Two ends of rods of length L and radius R of the same material of kept at the same temperature. Which of the following rods conducts the maximum heat?
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two copper wire of length l and 2l have radii, r and 2r respectively. What si the ratio of their specific resistance.?
A1:2B2:1C1:1D1:3 - Question 2 - Select One
The radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in length of the wire A is one percent, the percentage increase in length of the wire B is
A1.0B1.5C2.0D3.0 - Question 3 - Select One
Two vibrating strings of the same material but lengths L and 2L have radii 2 r and r respectively. They are strectched under the same tension. Both the strings vibrate in their fundamental modes, the one of length L with frequency n1 and the other with frequency n2. The ratio n1/n2 is given by
2
4
8
1A2B4C8D1
Two vibrating strings of the same material but lengths L and 2L have radii 2r and r respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length L with freuqency v1 and the other with frequency v2. the ratio v1/v2 is given by
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
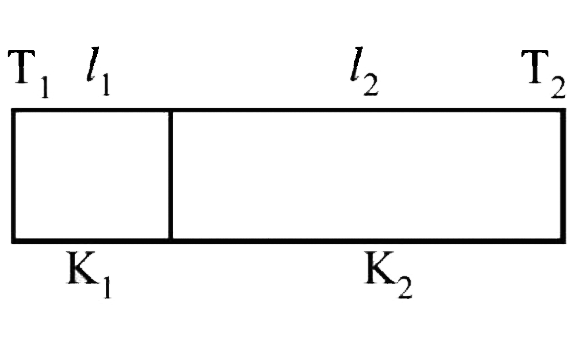 View Solution
View SolutionTwo spheres of same material and radius r and 2r are heated to same temperature and are kept in identical surroundings, ratio of their rate of loss of heat is
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View Solution

