Power factor is one for
pure inductor
pure capacitor
pure resistor
Either an inductor or a capacitor
The correct Answer is:C
To determine when the power factor is equal to 1, we need to analyze the relationship between resistance (R) and impedance (Z) in an AC circuit. The power factor (PF) is defined as:
Power Factor (PF)=RZ
Given that the power factor is 1, we can set up the equation:
PF=1⟹RZ=1⟹R=Z
Step 1: Understanding Impedance
The impedance (Z) of an LCR circuit is given by:
Z=√R2+(XL−XC)2
where:
- XL is the inductive reactance,
- XC is the capacitive reactance.
Step 2: Setting Up the Equation
From the power factor condition R=Z, we can substitute for Z:
R=√R2+(XL−XC)2
Step 3: Squaring Both Sides
To eliminate the square root, we square both sides:
R2=R2+(XL−XC)2
Step 4: Simplifying the Equation
Subtract R2 from both sides:
0=(XL−XC)2
Step 5: Analyzing the Result
The equation (XL−XC)2=0 implies:
XL−XC=0⟹XL=XC
This means that the inductive reactance equals the capacitive reactance, which occurs in a resonant circuit where both inductor and capacitor are present.
Step 6: Considering the Other Condition
Alternatively, if both the inductor and capacitor are absent, then:
XL=0andXC=0
In this case, the circuit is purely resistive, and the power factor will also be 1.
Conclusion
Thus, the power factor is 1 in two scenarios:
1. When both inductor and capacitor are present and in resonance (i.e., XL=XC).
2. When both inductor and capacitor are absent (i.e., the circuit is purely resistive).
Given the options:
1. Pure inductor
2. Pure capacitor
3. Pure resistor
4. Either an inductor or a capacitor
The correct answer is Option 3: Pure Resistor.
---
The impedance (Z) of an LCR circuit is given by:
- XL is the inductive reactance,
- XC is the capacitive reactance.
From the power factor condition R=Z, we can substitute for Z:
To eliminate the square root, we square both sides:
Subtract R2 from both sides:
The equation (XL−XC)2=0 implies:
Alternatively, if both the inductor and capacitor are absent, then:
Thus, the power factor is 1 in two scenarios:
1. When both inductor and capacitor are present and in resonance (i.e., XL=XC).
2. When both inductor and capacitor are absent (i.e., the circuit is purely resistive).
1. Pure inductor
2. Pure capacitor
3. Pure resistor
4. Either an inductor or a capacitor
Similar Questions
Power factor in series LCR circuit at reasonance is
View SolutionA : For a practicval choke coil the power factor is very small.
R : In a practical choke coil the power dissipation reduces if frequency of the a.c. is increased.
View SolutionThe power factor of the following circuit will be
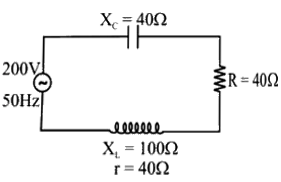
View SolutionPower factor of the circuit shown here is

View SolutionAt resonance, the value of the power factor in an LCR series circuit is
View SolutionPower factor in a series R-L-C resonant circuit is
View SolutionThe value of power factor coso in series LCR circuit at resonance is
View SolutionA circuit draws 330 W from a 110 V , 60 Hz AC line. The power factor is 0.6 and the current lags the voltage. The capacitance of a series capacitor that will result in a power factor of unity is equal to
View SolutionIf the power factor is 1/2 in a series RL circuit with R=100Ω. If AC mains, 50Hz is used then L is
View SolutionGiven below are two electric circuits A and B
Calculate the ratio of power factor of the circuit B to the power factor of circuit A.
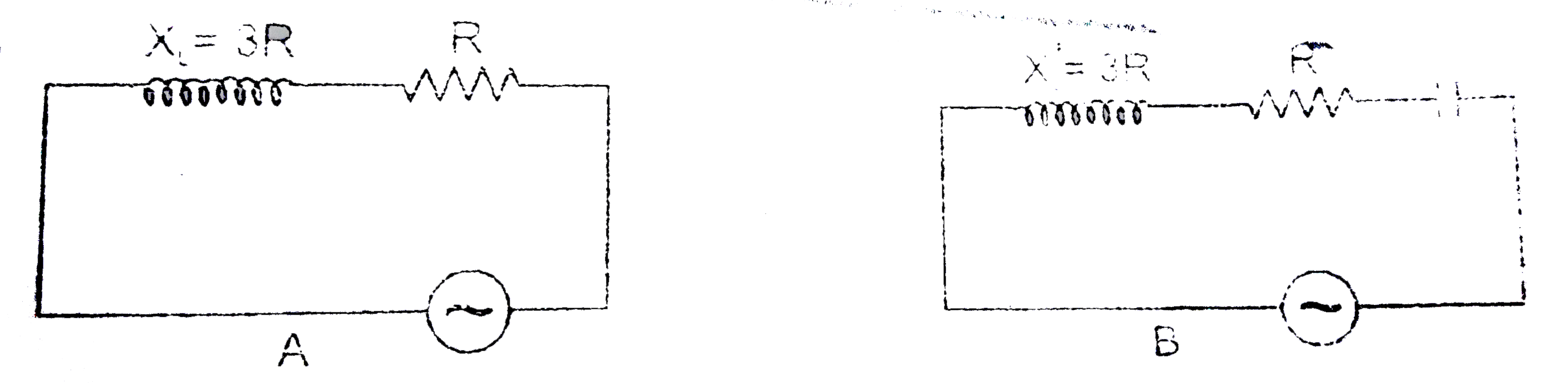
View Solution
