In an AC circuit, the power factor
is zero when the circuit contain an ideal resistance only
is unity when the circuit contains an ideal resistance only
is zero when the circuit contains an ideal inductance only
is unity when the circuit contains an ideal inductance only
The correct Answer is:B, C
To solve the question regarding the power factor in an AC circuit, we will analyze the provided options step by step.
Step 1: Understand the Power Factor
The power factor (PF) in an AC circuit is defined as:
Power Factor=cosϕ
where ϕ is the phase angle between the voltage and current. It can also be expressed in terms of resistance (R) and reactance (X):
Power Factor=R√R2+(XL−XC)2
Step 2: Analyze Each Option
Let's evaluate the options given in the question.
Option A: Power factor is zero when the circuit contains ideal resistance only.
- If the circuit contains only ideal resistance, then XL=0 and XC=0.
- Thus, the power factor becomes:
PF=R√R2=RR=1
- Therefore, this statement is incorrect.
Option B: Power factor is unity when the circuit contains ideal resistance only.
- As calculated above, when the circuit contains only resistance, the power factor is indeed:
PF=1
- Therefore, this statement is correct.
Option C: Power factor is 0 when the circuit contains ideal inductance only.
- If the circuit contains only an ideal inductor, then R=0 and XC=0.
- The power factor becomes:
PF=0√02+X2L=0
- Therefore, this statement is correct.
Option D: Power factor is unity when there is ideal inductance only.
- For an ideal inductor, the power factor is:
PF=0
- Therefore, this statement is incorrect.
Conclusion
From the analysis:
- Correct options are: B and C.
- Incorrect options are: A and D.
Final Answer
The correct options regarding the power factor in an AC circuit are B and C.
---
The power factor (PF) in an AC circuit is defined as:
Power Factor=cosϕ
where ϕ is the phase angle between the voltage and current. It can also be expressed in terms of resistance (R) and reactance (X):
Power Factor=R√R2+(XL−XC)2
Let's evaluate the options given in the question.
- If the circuit contains only ideal resistance, then XL=0 and XC=0.
- Thus, the power factor becomes:
PF=R√R2=RR=1
- Therefore, this statement is incorrect.
- As calculated above, when the circuit contains only resistance, the power factor is indeed:
PF=1
- Therefore, this statement is correct.
- If the circuit contains only an ideal inductor, then R=0 and XC=0.
- The power factor becomes:
PF=0√02+X2L=0
- Therefore, this statement is correct.
- For an ideal inductor, the power factor is:
PF=0
- Therefore, this statement is incorrect.
From the analysis:
- Correct options are: B and C.
- Incorrect options are: A and D.
The correct options regarding the power factor in an AC circuit are B and C.
Similar Questions
The potential differences across the resistance, capacitance and inductance are 80V,40V and 100V respectively in an L−C−R circuit. The power factor of this circuit is
View SolutionIf the frequency of the source e.m.f. in an AC circuit in n,the power varies with a frequency:
View SolutionGiven below are two electric circuits A and B
Calculate the ratio of power factor of the circuit B to the power factor of circuit A.
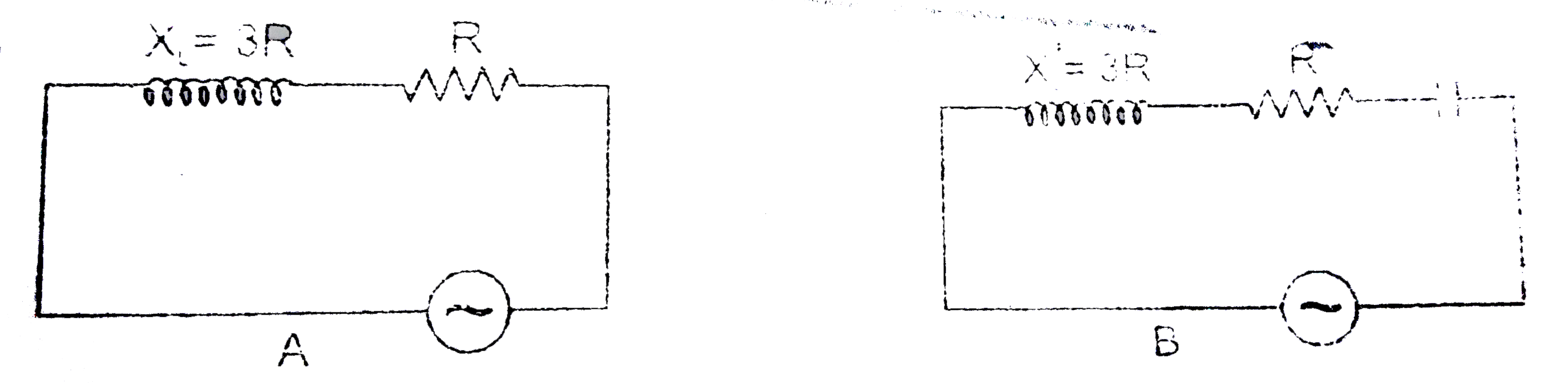 View Solution
View SolutionIn the given circuit, power factor between A and B is 0.5 and over all power factor of the circuit is 1.
Find the value of Rand L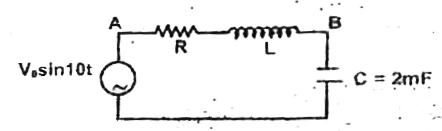 View Solution
View SolutionIn the circuit shown there is a box and capacitance C connected to alternating power source of angular frequency of 2 rad//s. Box has power factor 1/√2 and circuit has overall power factor 1
1. Find the impedance of the box View Solution
View SolutionIn the circuit shown there is a box containing a resistor and an inductor and the box in series with the capacitance C connected to alternating power source of frequency to 2 rad/s. Box has power factor 1√2 and circuit has overall power factor 1. The impedance of the box is
View SolutionA 60 cycle AC, circuit has a resistance of 200Ω and inductor of 100 mH. What is the power factor? What capacitance placed in the circuit will make the power factor unity?
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionIf V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
View SolutionIn the circuit shown in fin. Calculate the capacitance C of the capacitor, if the power factor of the circuit is unity. Also, calculate Q factor of the circuit.
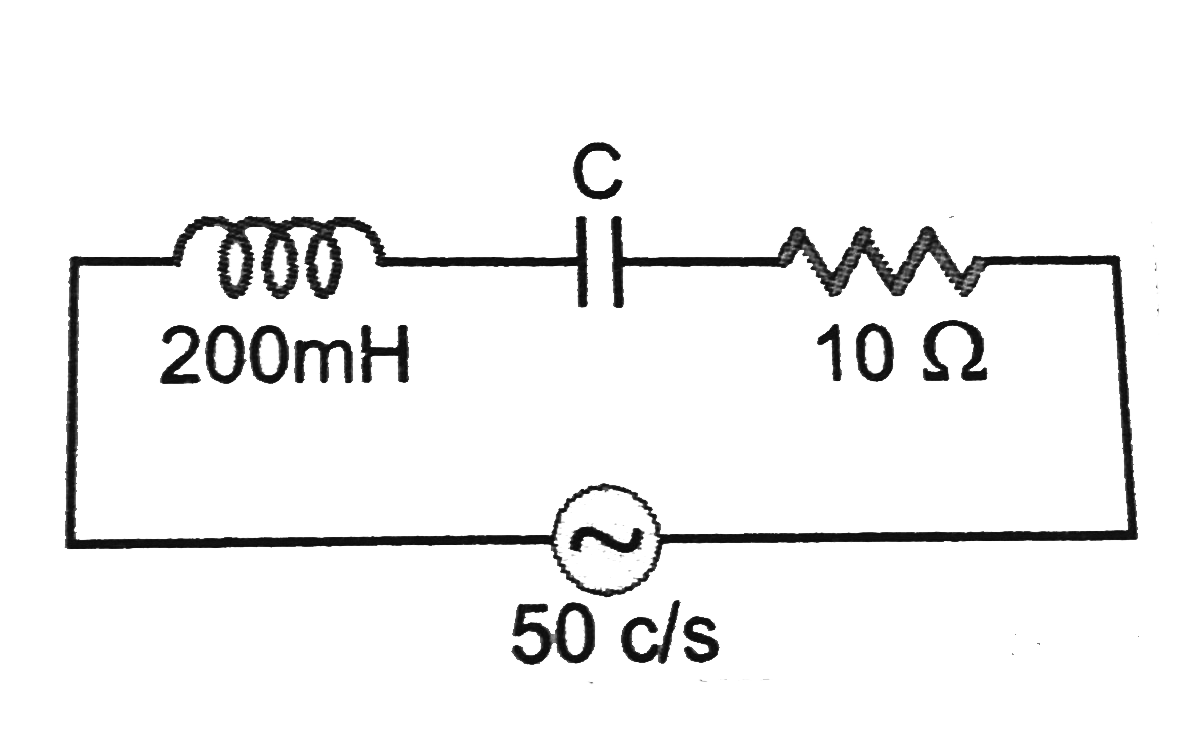 View Solution
View Solution

