If V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
V0I02
V0I0√2
V0I0cosθ
V0I02cosθ
The correct Answer is:D
To solve the problem, we need to derive the expression for the power dissipated in a series L-C-R circuit in terms of the peak current I0, peak voltage V0, and the power factor cosθ.
1. Understanding the Power in AC Circuits:
The power P dissipated in an AC circuit can be expressed as:
P=Vrms⋅Irms⋅cosθ
where Vrms is the root mean square voltage, Irms is the root mean square current, and cosθ is the power factor.
2. Relating Peak and RMS Values:
The relationship between the peak values and the RMS values is given by:
Vrms=V0√2andIrms=I0√2
where V0 is the peak voltage and I0 is the peak current.
3. Substituting RMS Values into the Power Formula:
Substitute the expressions for Vrms and Irms into the power formula:
P=(V0√2)⋅(I0√2)⋅cosθ
4. Simplifying the Expression:
Simplifying the expression gives:
P=V0⋅I02⋅cosθ
5. Final Expression for Power:
Therefore, the power dissipated in the circuit can be expressed as:
P=V0⋅I02⋅cosθ
Conclusion:
The power dissipated in a series L-C-R circuit is given by:
P=V0⋅I02⋅cosθ
The power P dissipated in an AC circuit can be expressed as:
P=Vrms⋅Irms⋅cosθ
where Vrms is the root mean square voltage, Irms is the root mean square current, and cosθ is the power factor.
The relationship between the peak values and the RMS values is given by:
Vrms=V0√2andIrms=I0√2
where V0 is the peak voltage and I0 is the peak current.
Substitute the expressions for Vrms and Irms into the power formula:
P=(V0√2)⋅(I0√2)⋅cosθ
Simplifying the expression gives:
P=V0⋅I02⋅cosθ
Therefore, the power dissipated in the circuit can be expressed as:
P=V0⋅I02⋅cosθ
The power dissipated in a series L-C-R circuit is given by:
P=V0⋅I02⋅cosθ
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2 Single Correct18videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 1 Assertion-Reason11videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
The power factor of a series LCR circuit is
View SolutionFor a series L C R circuit, the power loss at resonance is
View SolutionFor a series L C R circuit, the power loss at resonance is
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png) View Solution
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png) View Solution
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionPower factor in series LCR circuit at reasonance is
View SolutionIf in the circuit, power dissipation is 150W, the R is
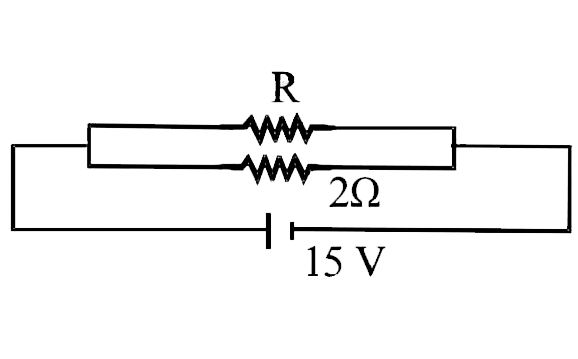 View Solution
View SolutionIn the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
View SolutionPower factor in a series R-L-C resonant circuit is
View Solution

