The peak value of an alternating emf E given by
E = Eo cos ωt
is 10 V and frequency is 50 Hz . At time t = (1/600) s, the instantaneous value of emf is
10 V
5√3 V
5 V
1 V
The correct Answer is:B
To find the instantaneous value of the alternating emf E at a specific time, we can follow these steps:
Step 1: Identify the given values
- The peak value of the alternating emf E0=10V
- The frequency f=50Hz
- The time t=1600s
Step 2: Calculate the angular frequency ω
The angular frequency ω is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100πrad/s
Step 3: Write the equation for instantaneous emf
The instantaneous value of the emf E is given by:
E=E0cos(ωt)
Step 4: Substitute the values into the equation
Substituting E0=10V, ω=100πrad/s, and t=1600s:
E=10cos(100π×1600)
Step 5: Simplify the argument of the cosine function
Calculating the argument:
100π×1600=100π600=π6
Thus, we have:
E=10cos(π6)
Step 6: Calculate the cosine value
We know that:
cos(π6)=cos(30∘)=√32
Now substituting this value back into the equation:
E=10×√32=5√3V
Step 7: Final answer
The instantaneous value of the emf at t=1600s is:
E=5√3V
- The peak value of the alternating emf E0=10V
- The frequency f=50Hz
- The time t=1600s
The angular frequency ω is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100πrad/s
The instantaneous value of the emf E is given by:
E=E0cos(ωt)
Substituting E0=10V, ω=100πrad/s, and t=1600s:
E=10cos(100π×1600)
Calculating the argument:
100π×1600=100π600=π6
Thus, we have:
E=10cos(π6)
We know that:
cos(π6)=cos(30∘)=√32
Now substituting this value back into the equation:
E=10×√32=5√3V
The instantaneous value of the emf at t=1600s is:
E=5√3V
Similar Questions
The peak value of an alternating emf E given by
E=(E0)cosωt
is 10V and frequency is 50 Hz. At time t=(1/600)s the instantaneous value of emf is
View SolutionAn inductor (L=200mH) is connected to an AC source of peak emf210V and frequency 50Hz. Calculate the peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View SolutionAn inductor (L=200mH) is connected to an AC source of peak emf 210V and frequency 50Hz. Calculate the peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View SolutionAn AC voltage is given by E = Eo sin 2πt / T
Then , the mean value of volatage calculated over any time interval of T / 2
View SolutionThe alternating current in a circuit is given by I=50sin314t. The peak value and frequency of the current are
View SolutionTwo coils have a mutual inductance 0.005 H. The alternating current changes in the first coil according to equation I = Iosinωt, where Io = 10 A and ω = 100π rads−1. The maximum value of emf in the second coil
is (in volt)
View SolutionThe root-mean-square value of an alternating current of 50 Hz frequency is 10 ampere. The time taken by the alternating current in reaching from zero to maximum value and the peak value of current will be
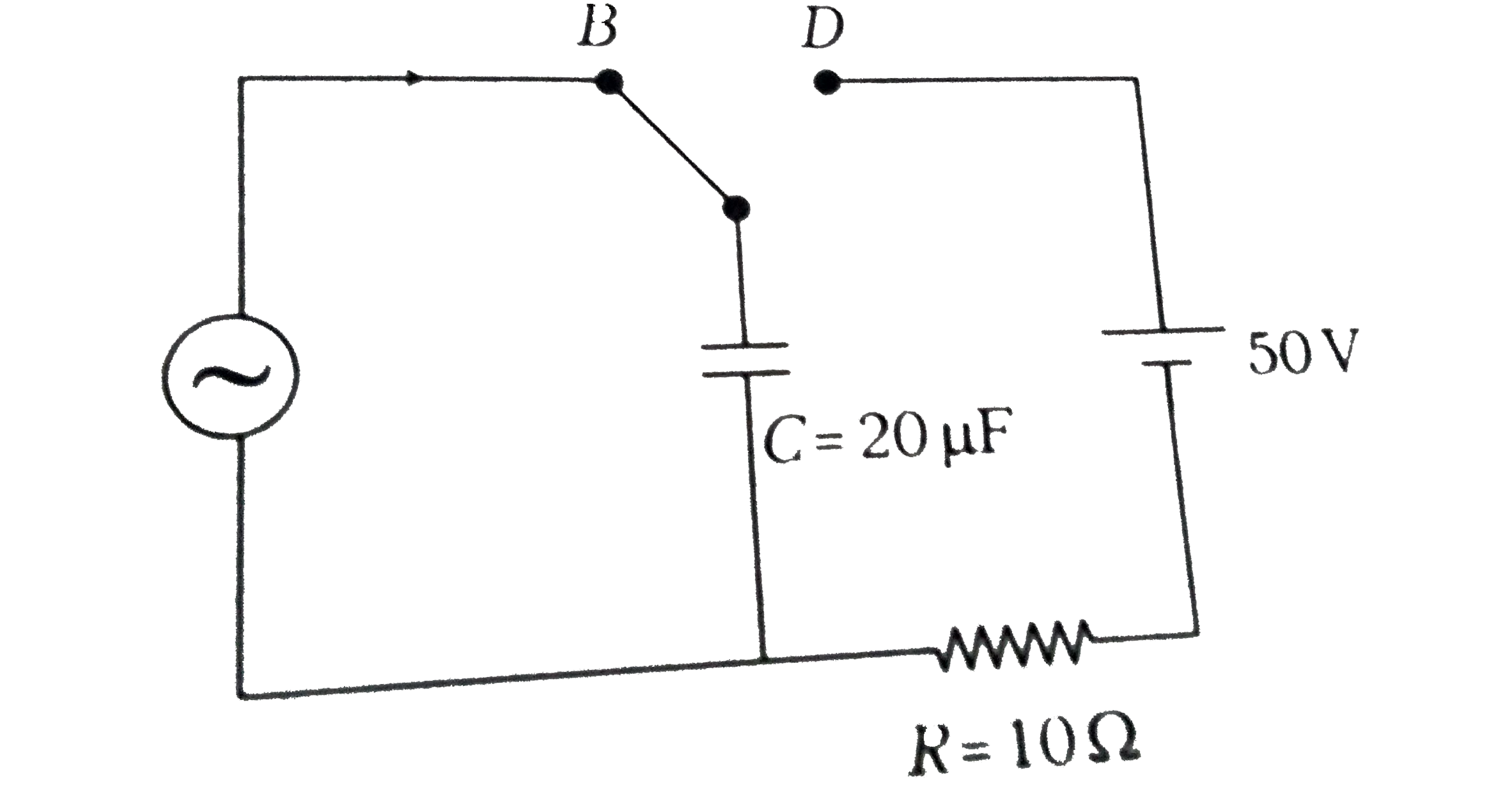
View SolutionAt time t = 0 , terminal A in the circuit shown in the figure is connected to B by a key and alternating current I(t) = Iocos(ωt), with Io = 1 A and ω = 500 rads−1 starts flowing in it with the initial direction shown in the figure . At t = 7π/6ω , the keys is switched from B to D . Now onwards only A and D are connected . A total charge Q flows from the battery to charge the capacitor fully. If C = 20 μ , R = 10 Ω and the battery is deal with emf of 50 V , identify the correct statement(s).
View SolutionAn alternating voltage is given by: e=e1sinωt+e2cosωt. Then the root mean square value of voltage is given by:
View SolutionAn alternating voltage is given by: e=e1sinωt+e2cosωt. Then the root mean square value of voltage is given by:
View Solution
