The alternating current in a circuit is given by I=50sin314t. The peak value and frequency of the current are
I0=25 A and f=100Hz
I0=50 A and f=50 Hz
I0 = 50 A and f=100 Hz
I0=25 A and f=50 Hz
The correct Answer is:B
To solve the problem, we need to determine the peak value and frequency of the alternating current given by the equation I=50sin(314t).
1. Identify the given equation:
The alternating current is given by:
I=50sin(314t)
2. Compare with the standard form:
The standard form of an alternating current is:
I=I0sin(ωt)
where I0 is the peak current (amplitude) and ω is the angular frequency.
3. Determine the peak current I0:
From the equation I=50sin(314t), we can see that:
I0=50A
Thus, the peak value of the current is 50A.
4. Find the angular frequency ω:
From the equation, we have:
ω=314rad/s
5. Calculate the frequency f:
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Rearranging this gives:
f=ω2π
Substituting the value of ω:
f=3142π
6. Calculate f:
Using π≈3.14:
f=3142×3.14=3146.28≈50Hz
Final Results:
- The peak value I0 is 50A.
- The frequency f is 50Hz.
Summary:
The peak value of the current is 50A and the frequency is 50Hz.
The alternating current is given by:
I=50sin(314t)
The standard form of an alternating current is:
I=I0sin(ωt)
where I0 is the peak current (amplitude) and ω is the angular frequency.
From the equation I=50sin(314t), we can see that:
I0=50A
Thus, the peak value of the current is 50A.
From the equation, we have:
ω=314rad/s
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Rearranging this gives:
f=ω2π
Substituting the value of ω:
f=3142π
Using π≈3.14:
f=3142×3.14=3146.28≈50Hz
- The peak value I0 is 50A.
- The frequency f is 50Hz.
The peak value of the current is 50A and the frequency is 50Hz.
Similar Questions
An alternating current in a circuit is given by l = 20 sin ( 100πt + 0.05π) A. The rms value and the frequency of current respectively are
View SolutionThe value of current I in the circuit will be
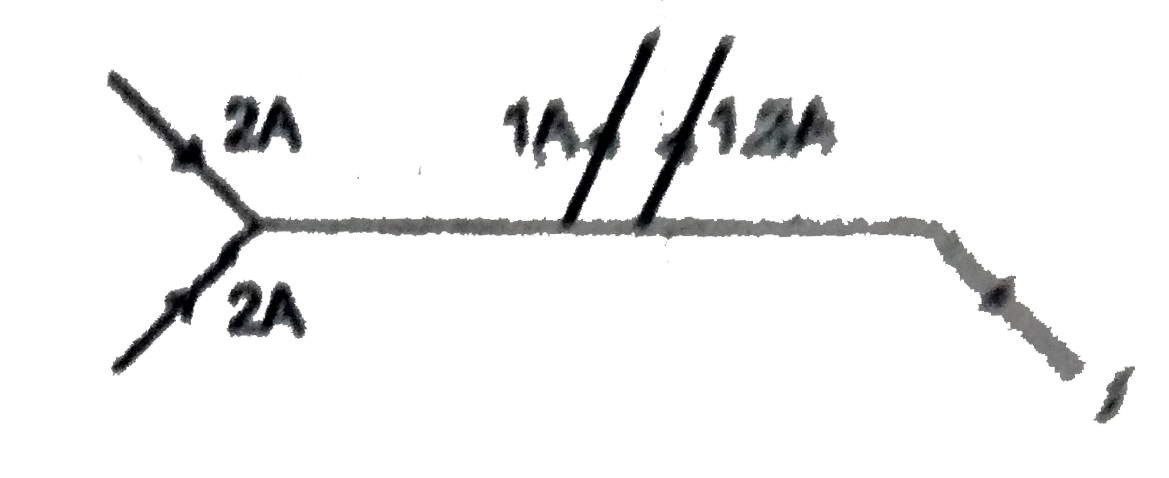
View SolutionThe current 'i' in the given circuit is
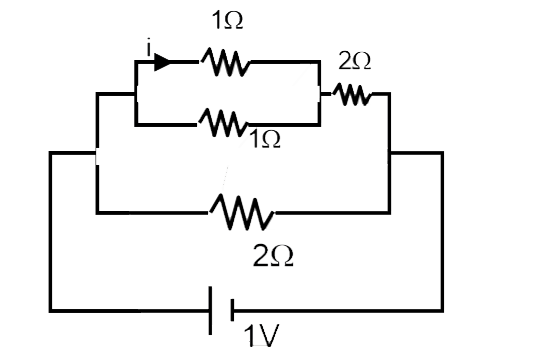
View SolutionThe current (i) in the given circuit is

View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionThe electric current in AC circuit is given by the relation i =3sinωt+4cosωt. The rms value of the current in the circuit in ampere is
View SolutionIf instantaneous current in a circuit is given by I=(2+3sinωt) A, then the effective value of resulting current in the circuit is
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s is
View SolutionThe peak value of an alternating current is 5A and its frequency is 60Hz. The rms value and the time taken by current take to reach the peak value starting from zero is:
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View Solution
