The resonant frequency of a circuit is f. If the capacitance is made 4 times the initial values, then the resonant frequecy will become
f/2
2f
f
f/4
The correct Answer is:A
To solve the problem, we need to understand the relationship between the resonant frequency of an LRC circuit and the capacitance. The resonant frequency f is given by the formula:
f=12π√LC
where:
- L is the inductance,
- C is the capacitance.
1. Identify the initial resonant frequency:
The initial resonant frequency is given as f0 when the capacitance is C0:
f0=12π√LC0
2. Change the capacitance:
According to the problem, the capacitance is increased to four times its initial value:
C=4C0
3. Calculate the new resonant frequency:
Substitute the new capacitance into the resonant frequency formula:
f=12π√L(4C0)
4. Simplify the expression:
We can factor out the 4 from the square root:
f=12π√L⋅√4C0=12π√L⋅2√C0=14π√LC0
5. Relate the new frequency to the initial frequency:
Notice that:
14π√LC0=12⋅12π√LC0=f02
Therefore, the new resonant frequency f is:
f=f02
6. Conclusion:
The new resonant frequency when the capacitance is made four times the initial value is half of the original frequency:
f=f02
Final Answer:
The resonant frequency will become f2.
- L is the inductance,
- C is the capacitance.
The initial resonant frequency is given as f0 when the capacitance is C0:
f0=12π√LC0
According to the problem, the capacitance is increased to four times its initial value:
C=4C0
Substitute the new capacitance into the resonant frequency formula:
f=12π√L(4C0)
We can factor out the 4 from the square root:
f=12π√L⋅√4C0=12π√L⋅2√C0=14π√LC0
Notice that:
14π√LC0=12⋅12π√LC0=f02
Therefore, the new resonant frequency f is:
f=f02
The new resonant frequency when the capacitance is made four times the initial value is half of the original frequency:
f=f02
The resonant frequency will become f2.
Similar Questions
Knowledge Check
- Question 1 - Select One
The resonant frequency of a series LCR circuit with L=2.0H,C=32μF and R=10Ω is
A20 HzB30 HzC40 HzD50 Hz - Question 2 - Select One
To reduce the resonant frequency in an LCR series circuit with a generator
Athe generator frequency should be reduced.Banother capacitor should be added in parallel to the first.Cthe iron core of the inductor should be removed.Ddielectric in the capacitor should be removed.
To reduce the resonant frequency in an LCR series circuit with a generator
View SolutionTo reduce the resonant frequency in an LCR series circuit with a generator
View SolutionFind the resonant frequency of a series circuit consist of an inductance 200 μH, a capacitance of 0.0005μF and a resistance of 10 Ω.
View SolutionAn ac generator G with an adjustable frequency of oscillation is used in the circuit, as shown.
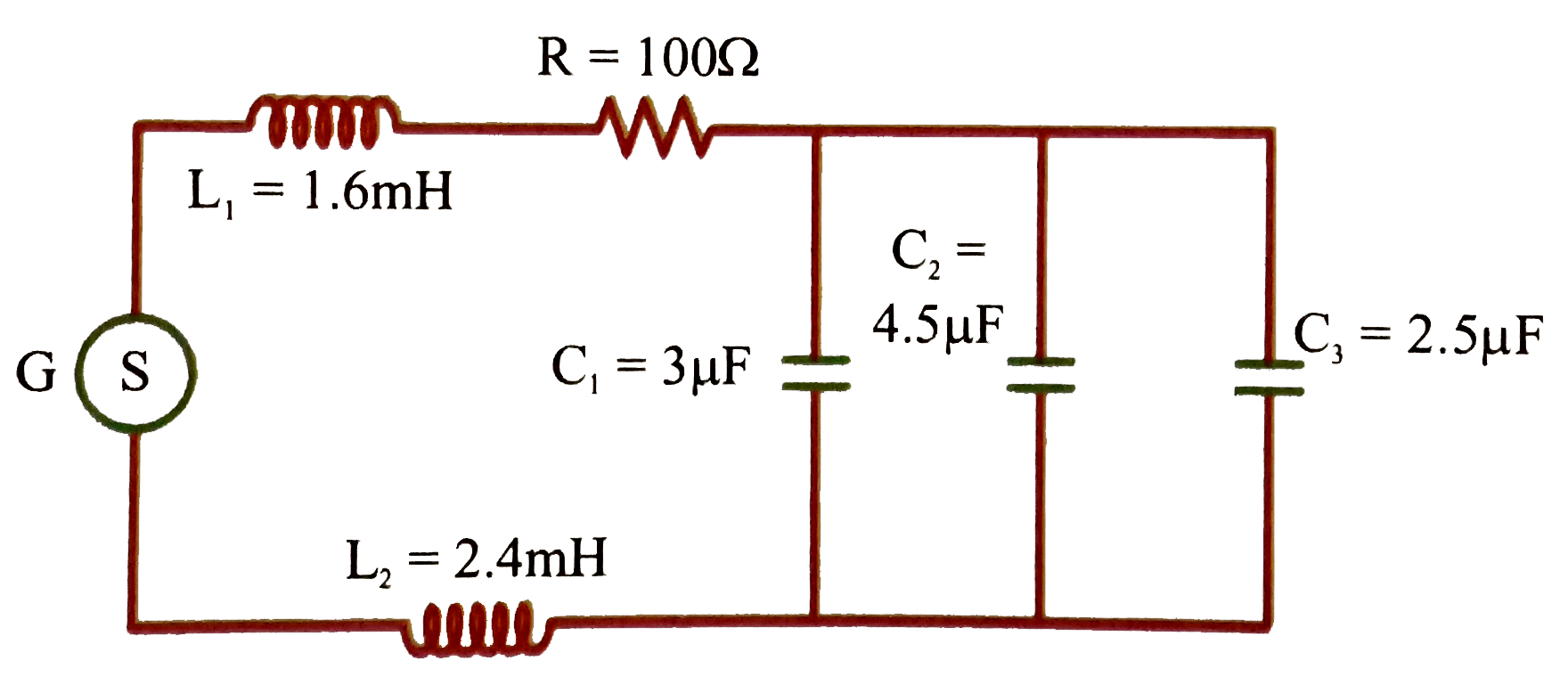
To increase resonant frequency of the circuit, some of the changes in the circuit are carried out. Which changes would certainly result in the increase in resonant frequency ?View SolutionThe current graph for resonance in LC circuit is
View SolutionAn ac generator G with an adjustable frequency of oscillation is used in the circuit, as shown.

To increase resonant frequency of the circuit, some of the changes in the circuit are carried out. Which changes would certainly result in the increase in resonnatn frequency ?View Solution

