In a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
To solve the problem step-by-step, we will first find the resonance frequency and then calculate the current at that frequency.
Step 1: Determine the resonance frequency
The resonance frequency (ω) in a series L-C-R circuit is given by the formula:
ω=1√LC
Where:
- L is the inductance in henries (H)
- C is the capacitance in farads (F)
Step 2: Convert the given values to standard units
Given:
- L=8 milli henry = 8×10−3 H
- C=20 micro farad = 20×10−6 F
Step 3: Substitute the values into the formula
Now we substitute the values of L and C into the resonance frequency formula:
ω=1√(8×10−3)(20×10−6)
Step 4: Calculate the product LC
First, we calculate LC:
LC=(8×10−3)×(20×10−6)=160×10−9=1.6×10−7 H.F
Step 5: Calculate ω
Now, we can find ω:
ω=1√1.6×10−7
Calculating the square root:
√1.6×10−7≈4.0×10−4
Thus,
ω≈14.0×10−4=2500 rad/s
Step 6: Calculate the current at resonance
At resonance, the current I can be calculated using Ohm's Law:
I=VR
Where:
- V=220 volts
- R=44 ohms
Step 7: Substitute the values into the current formula
Now we substitute the values:
I=22044
Step 8: Calculate the current
Calculating the current:
I=5 A
Final Answers
- Resonance frequency ω=2500 rad/s
- Current at resonance I=5 A
---
The resonance frequency (ω) in a series L-C-R circuit is given by the formula:
- L is the inductance in henries (H)
- C is the capacitance in farads (F)
Given:
- L=8 milli henry = 8×10−3 H
- C=20 micro farad = 20×10−6 F
Now we substitute the values of L and C into the resonance frequency formula:
First, we calculate LC:
Now, we can find ω:
At resonance, the current I can be calculated using Ohm's Law:
- V=220 volts
- R=44 ohms
Now we substitute the values:
Calculating the current:
- Resonance frequency ω=2500 rad/s
- Current at resonance I=5 A
Similar Questions
For the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency

View SolutionFor the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency
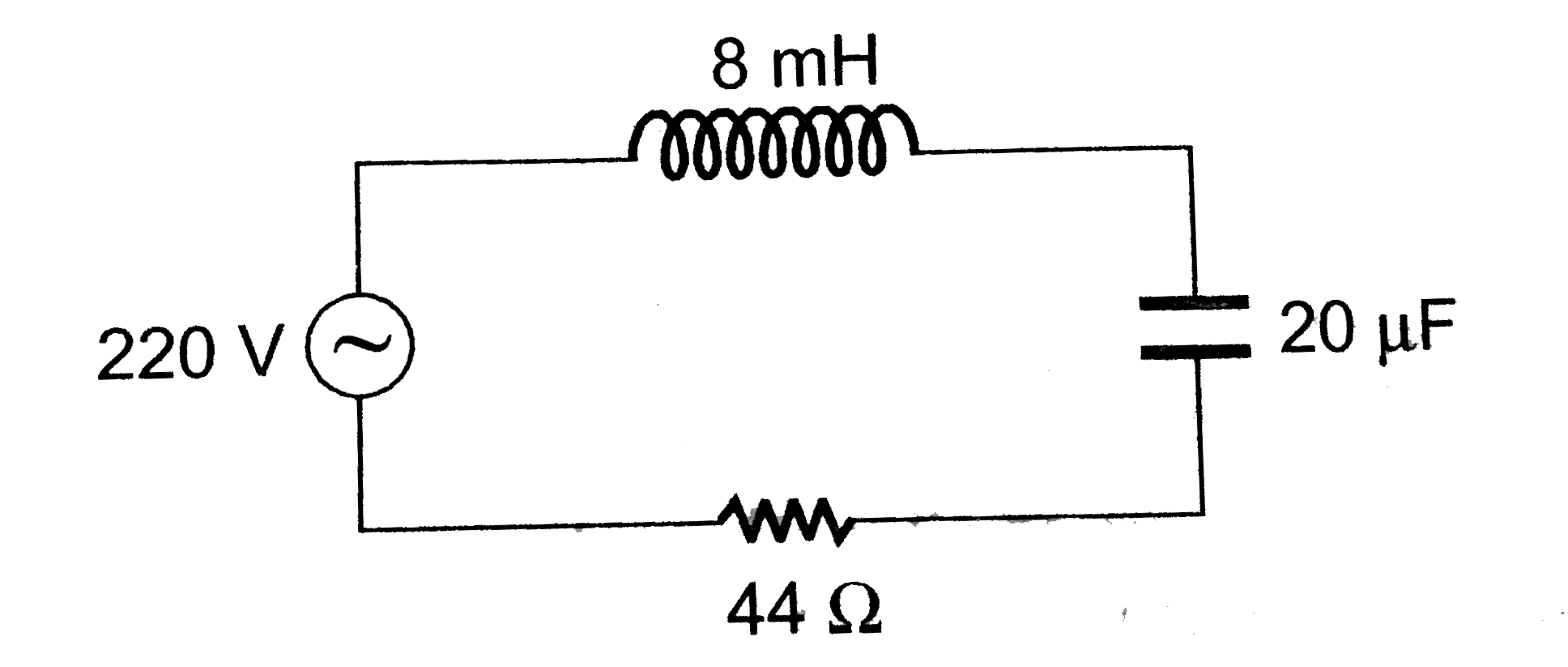
View Solution
Knowledge Check
At resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinity
Current through an AC series L-C-R circuit is 2 A if operated at resonance frequency , and 1 A if operated at 50% less than resonant frequency . The current (in A) if the frequency is 100% more than the resonant frequency , is
A.√2 B.1 C.√3 D.Data insufficient
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionIn a series LCR circuit, obtain an expression for the resonant frequency.
View SolutionAssertion : In series L−C−R circuit, voltage will lead the current function for frequency greater than the resonance frequency.
Reason : At resonance frequency, phase difference between current function and voltage function is zero.
View SolutionIn an L-C-R series, AC circuit at resonance
View SolutionAn L-C-R series circuit , connected to a source E, is at resonance. Then,
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.

View Solution