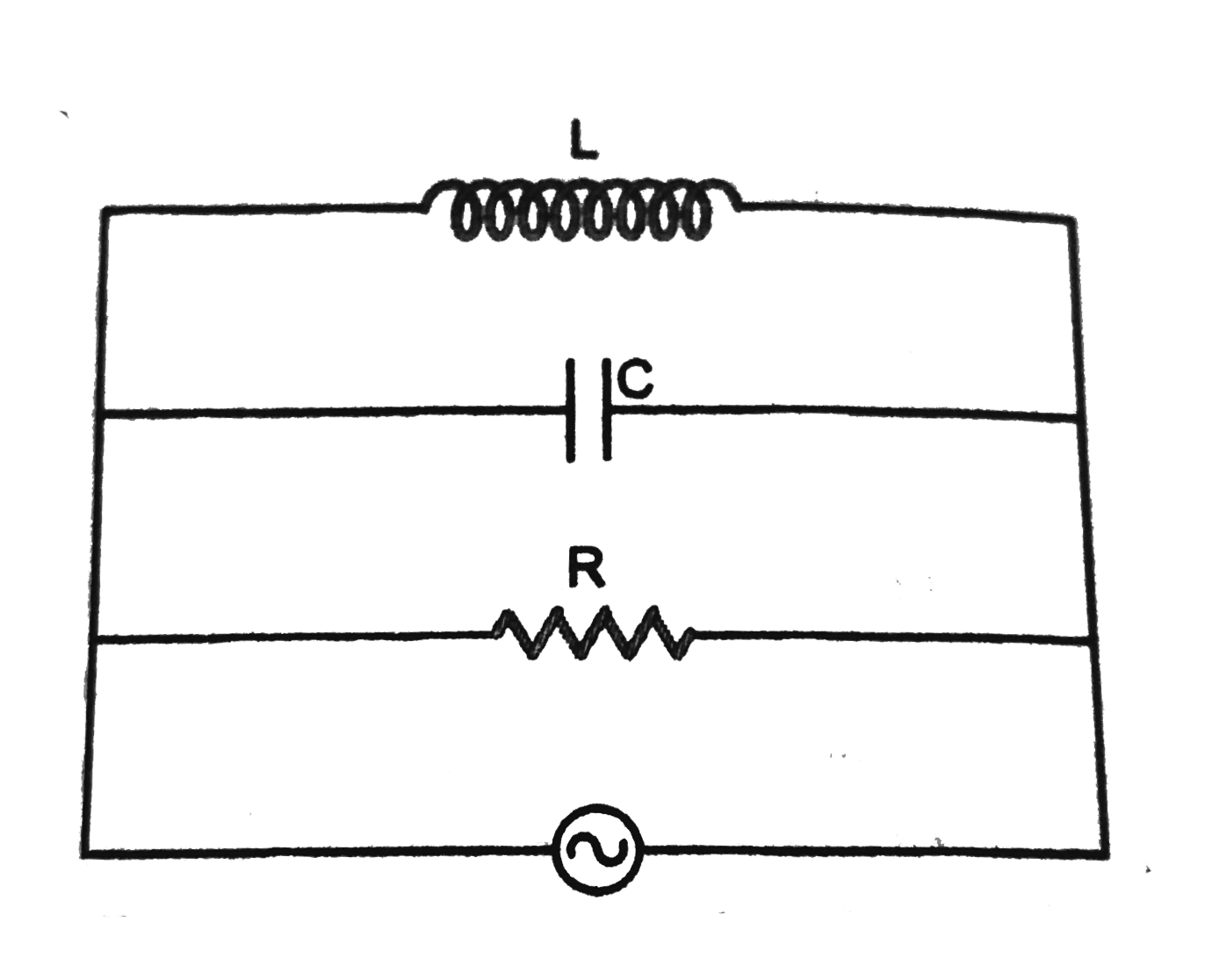
Resonant frequency is given by (for a series L-C-R circuit)
2π√LC
12π√LC
2π√LC
12π√LC
The correct Answer is:D
To find the resonant frequency of a series L-C-R circuit, we can follow these steps:
1. Understand the Components: In a series L-C-R circuit, we have three main components:
- L: Inductance (measured in Henrys)
- C: Capacitance (measured in Farads)
- R: Resistance (measured in Ohms)
2. Identify Reactances: At resonance, the inductive reactance (XL) and capacitive reactance (XC) are equal:
- Inductive Reactance: XL=ωL
- Capacitive Reactance: XC=1ωC
3. Set Reactances Equal: At resonance, we set XL equal to XC:
ωL=1ωC
4. Rearrange the Equation: Multiply both sides by ω to eliminate the fraction:
ω2L=1C
5. Solve for Omega: Rearranging gives us:
ω2=1LC
Taking the square root of both sides results in:
ω=1√LC
6. Convert Omega to Frequency: The relationship between angular frequency (ω) and frequency (f) is given by:
f=ω2π
Substituting for ω:
f=12π√LC
7. Final Expression: The resonant frequency f of the series L-C-R circuit is:
f=12π√LC
- L: Inductance (measured in Henrys)
- C: Capacitance (measured in Farads)
- R: Resistance (measured in Ohms)
- Inductive Reactance: XL=ωL
- Capacitive Reactance: XC=1ωC
ωL=1ωC
ω2L=1C
ω2=1LC
Taking the square root of both sides results in:
ω=1√LC
f=ω2π
Substituting for ω:
f=12π√LC
f=12π√LC
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
At resonance frequency the impedance in series LCR circuit is
AmaximumBminimumCzeroDinfinity - Question 2 - Select One
In L−C−R series circuit
Acurrent may achieve same value for two different value of frequencyBcurrent can not achieve same value for two different values of frequencyCcurrent is maximum for a maximum value of frequencyDnone of these - Question 3 - Select One
The resonant frequency of a series LCR circuit with L=2.0H,C=32μF and R=10Ω is
A20 HzB30 HzC40 HzD50 Hz
Obtain the resonant frequency 0, of a series LCR circuit with L = 2.0 H, C = 32 uF and R = 10 Ω . What is the Q-value of this circuit?
View SolutionKeeping the source of frequency equal to the resonating frequency of the series LCR circuit, if the three elements L, C and R in are arranged in parallel , show that the total current in the parallel LCR circuit is a minimum at this frequency. Obtain the r.m.s. value of current in each brach of the circuit for the elements and source specified in for this frequency.
 View Solution
View SolutionAt resonant frequency the current amplitude in series LCR circuit is
View SolutionIn L−C−R series AC circuit,
View SolutionThe figure shows variation of R,XL and XC with frequency f in a series L,C,R circuit. Then for what frequency point, the circuit is inductive ?
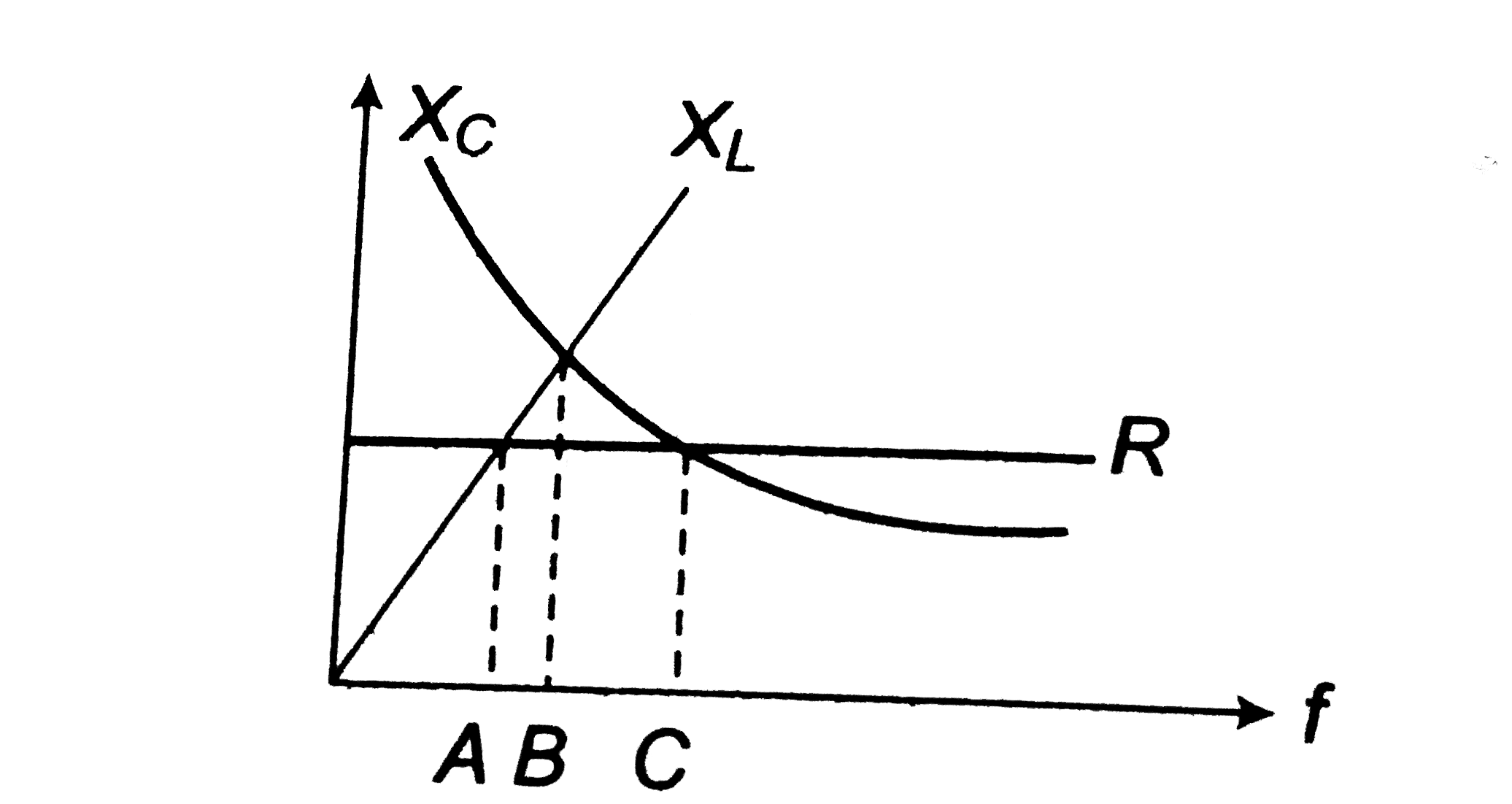 View Solution
View Solution

