If the reflected ray is rotated by an angle of in clockwisse direction then the mirror was rotated by
in anti-clockwise direction
in anti-clockwise direction
in clockwise direction
in clockwise direction
The correct Answer is:A
To solve the problem, we need to understand the relationship between the rotation of a mirror and the rotation of the reflected ray.
1. Understand the relationship: When a plane mirror is rotated by an angle α, the angle of the reflected ray changes by 2α. This is a fundamental property of reflection in optics.
2. Identify the given information: According to the problem, the reflected ray is rotated by an angle of 4θ in the clockwise direction.
3. Set up the equation: Since the reflected ray rotates by 2α, we can set up the equation:
2α=4θ
4. Solve for α: To find the angle by which the mirror was rotated, we divide both sides of the equation by 2:
α=4θ2=2θ
5. Determine the direction of rotation: The problem states that the reflected ray is rotated in the clockwise direction. Since the mirror's rotation is opposite to the direction of the reflected ray's rotation, the mirror must be rotated in the anticlockwise direction.
6. Conclusion: Therefore, the mirror was rotated by 2θ in the anticlockwise direction.
Final Answer:
The mirror was rotated by 2θ in the anticlockwise direction.
---
2α=4θ
α=4θ2=2θ
The mirror was rotated by 2θ in the anticlockwise direction.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.3
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A complex number z is rotated in anticlockwise direction by an angle α and we get z' and if the same complex number z is rotated by an angle α in clockwise direction and we get z''then
View SolutionShow that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
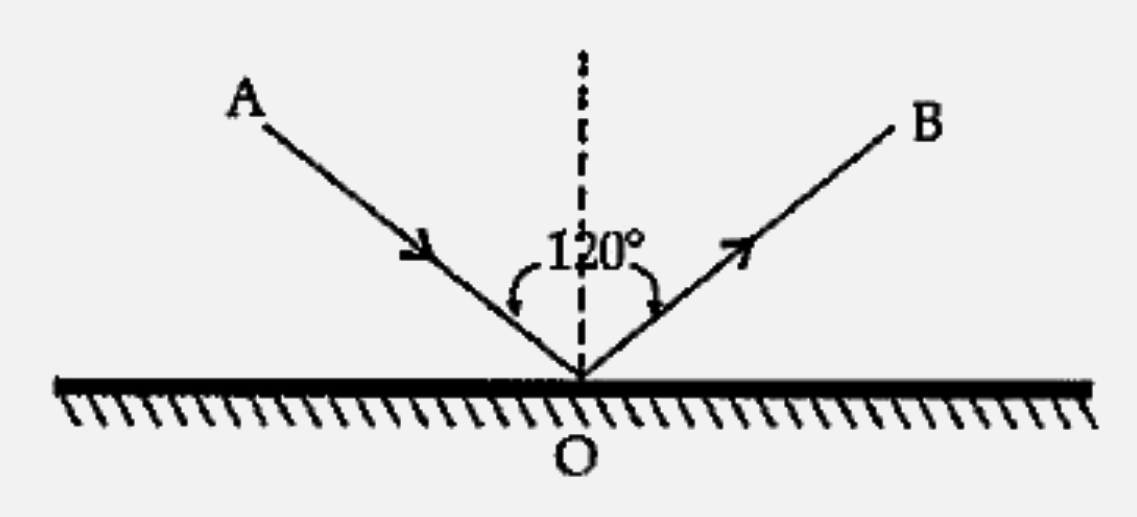
If the image of an object is formed 5 cm behind the mirror, what is the distance between the image and the object?
View SolutionA vector 3i + 4j rotates about its tail through an angle 37° in anticlockwise direction then the new vector is
View Solutiona ray of light is incident on a plane miror at an angle of 30∘ in anti-clockwise direction. Find the angle and sense of rotation of the reflected ray.

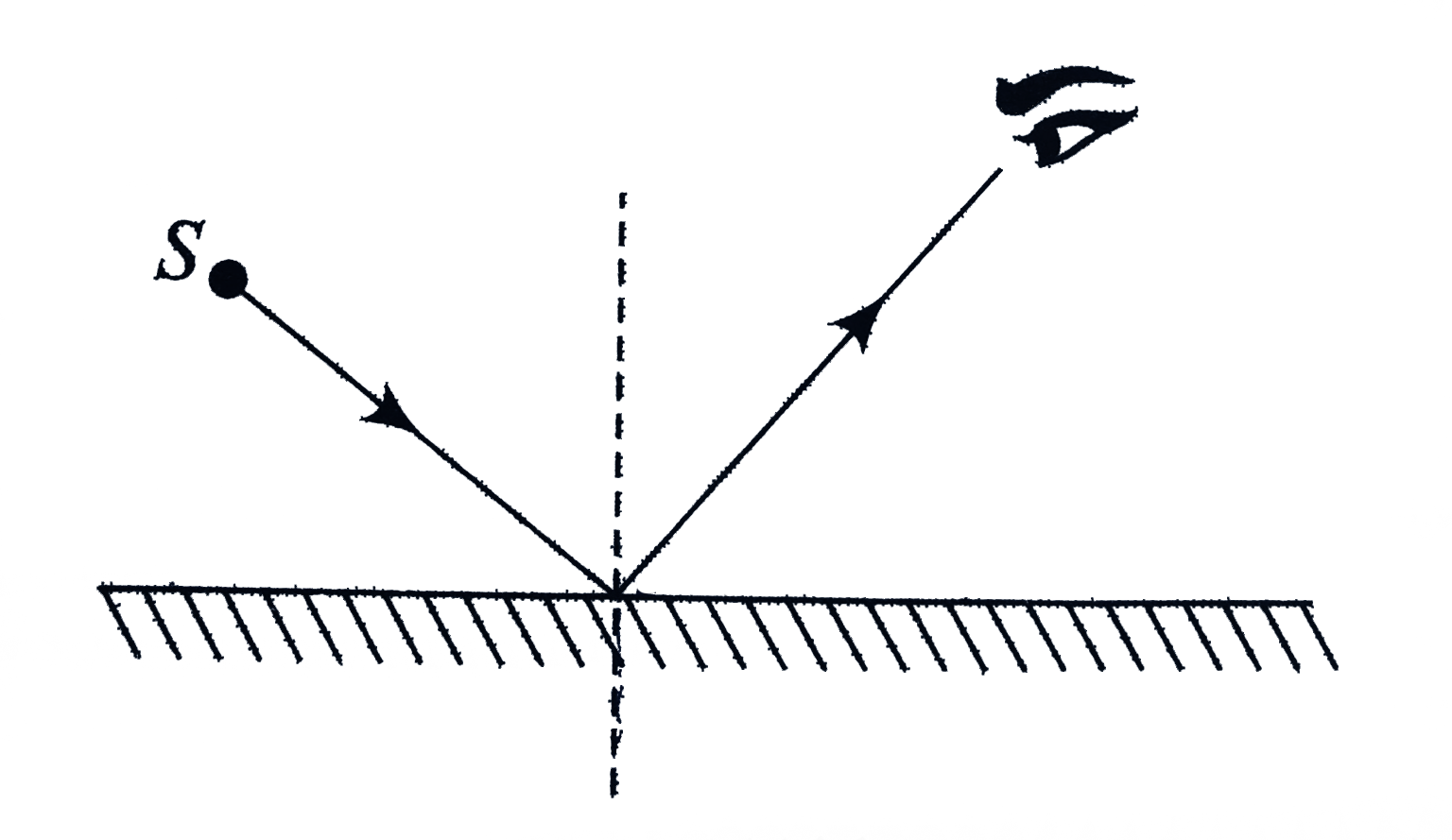
View SolutionA ray of light travels from a light source S to an observer after reflection from a plane mirror. If the source rotates in the clockwise direction by 10∘, by what angle and is what direction must the mirror be rotated so that the light ray still strikes the observer?
View SolutionAngle of a line with the positive direction of the x-axis is θ . The line is rotated about some point on it in anticlockwise direction by angle 450 and its slope becomes 3. Find the angle θ.
View SolutionAngle of a line with the positive direction of the x-axis is θ . The line is rotated about some point on it in anticlockwise direction by angle 450 and its slope becomes 3. Find the angle θ.
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
View SolutionIn the shown figure, mirror is rotated by an angle theta. Find theta if
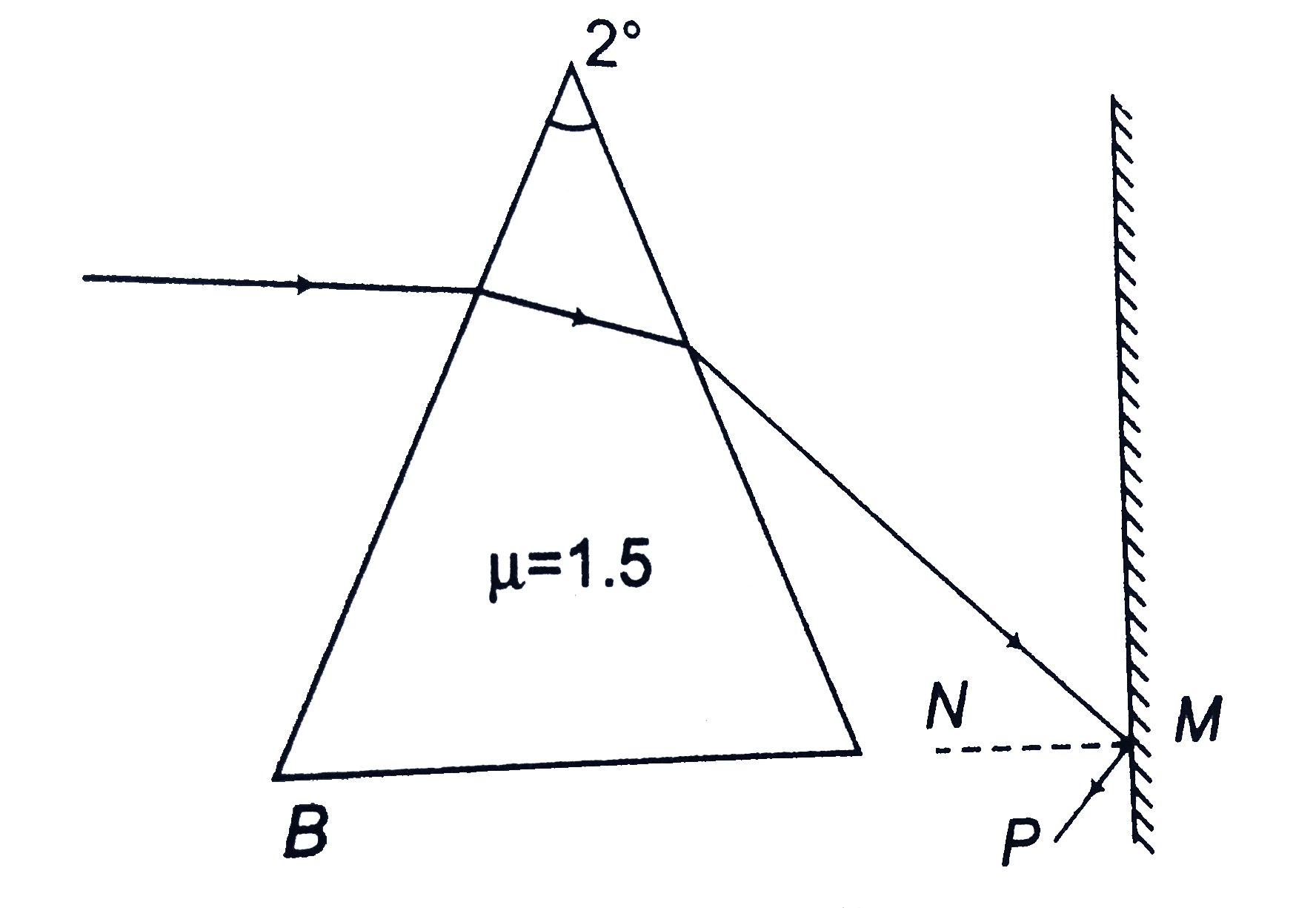
ray of light retraces its path after reflection from M
ray of light MP turns in the direction of MN.
View Solution
