An object is moving towards a stationary plane mirror with a speed of 2 m/s. Velocity of the image w.r.t. the object is
2 m/s towards right
4 m/s towards right
2 m/s towards left
4 m/s towards left
The correct Answer is:D
To solve the problem of finding the velocity of the image with respect to the object when the object is moving towards a stationary plane mirror, we can follow these steps:
1. Understand the Motion:
- The object is moving towards the plane mirror with a speed of 2 m/s.
2. Identify the Velocity of the Image:
- For a plane mirror, the image moves in the opposite direction to the object but with the same speed. Therefore, if the object moves towards the mirror at 2 m/s, the image will also appear to move towards the mirror at 2 m/s.
3. Determine the Direction:
- Since the object is moving towards the mirror, we can consider the direction towards the mirror as negative. Thus, the velocity of the object (v_object) can be represented as:
vobject=−2m/s
- The velocity of the image (v_image) will be:
vimage=2m/s(towards the mirror)
- However, since the image is also moving towards the mirror, we can represent its velocity as:
vimage=−2m/s
4. Calculate the Velocity of the Image with Respect to the Object:
- The relative velocity of the image with respect to the object (v_image/object) can be calculated using the formula:
vimage/object=vimage−vobject
- Substituting the values:
vimage/object=(−2m/s)−(−2m/s)=−2m/s−(−2m/s)=−2m/s+2m/s=−4m/s
5. Interpret the Result:
- The negative sign indicates that the image is moving towards the left with respect to the object. Thus, the velocity of the image with respect to the object is 4 m/s towards the left.
Final Answer:
The velocity of the image with respect to the object is 4 m/s towards the left.
- The object is moving towards the plane mirror with a speed of 2 m/s.
- For a plane mirror, the image moves in the opposite direction to the object but with the same speed. Therefore, if the object moves towards the mirror at 2 m/s, the image will also appear to move towards the mirror at 2 m/s.
- Since the object is moving towards the mirror, we can consider the direction towards the mirror as negative. Thus, the velocity of the object (v_object) can be represented as:
vobject=−2m/s
- The velocity of the image (v_image) will be:
vimage=2m/s(towards the mirror)
- However, since the image is also moving towards the mirror, we can represent its velocity as:
vimage=−2m/s
- The relative velocity of the image with respect to the object (v_image/object) can be calculated using the formula:
vimage/object=vimage−vobject
- Substituting the values:
vimage/object=(−2m/s)−(−2m/s)=−2m/s−(−2m/s)=−2m/s+2m/s=−4m/s
- The negative sign indicates that the image is moving towards the left with respect to the object. Thus, the velocity of the image with respect to the object is 4 m/s towards the left.
The velocity of the image with respect to the object is 4 m/s towards the left.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.3
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
Knowledge Check
A plane mirror is placed along the x-axis facing negative y-axis. The mirror is fixed, A point object is moving with 3ˆi+4ˆj in front of the plane mirror. The relative velocity of image with respect to its object is
 A−8ˆjB8ˆjC3ˆi−4ˆjD−6ˆi
A−8ˆjB8ˆjC3ˆi−4ˆjD−6ˆi
A real object is moving toward a fixed spherical mirror. The image
View SolutionWhat will be the image speed if
(i) Object is moving towards the plane mirror with speed v ?
(ii) The plane mirror is moving towards the object with speed v ?
View SolutionA linear object AB is placed along the axis of a concave mirror. This object is moving towards the mirror with speed U. The speed of the image of the point A is 4U and the speed of the image of B is alSO 4U btu in opposite direction. If the center of the line AB is at a distance L from the mirror then find out the length of the object.

View Solution
If an object moves towards a plane mirror with a speed v at an angle θ to the perpendicular to the plane of the mirror, find the relative velocity between the object and the image.
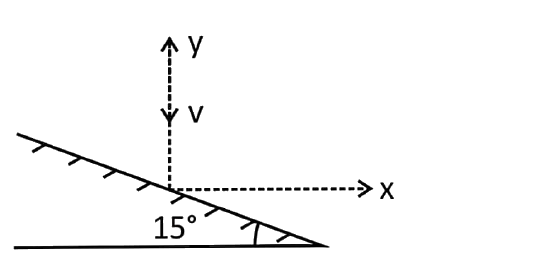
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
View SolutionA point object is moving towards a plane mirror as shown in figure. Choose the correct options.

View SolutionA point object is moving along principal axis of concave mirror with uniform velocity towards pole. Initially the object is at infinite distance from pole right side of the mirror as shown. Before the object collides with mirror, the number of times a which the distance between object and its image is 40cm are.
 .
.
View Solution